Перемножители аналоговых сигналов

Перемножители аналоговых сигналов (ПАС) предназначены для получения произведения двух аналоговых сигналов, которое будем называть откликом'.

I.

где К_м = const — масштабный коэффициент.

В большинстве случаев перемножаемыми сигналами являются гармонические колебания (напряжения, токи) с постоянными или медленно меняющимися во времени параметрами (амплитудой, частотой, фазой):

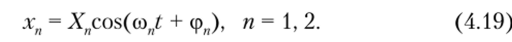I.

Такие ПАС называют смесителями. После подстановки соотношений (4.19) в равенство (4.18) получим отклик в виде составляющих с суммарной и разностной частотами:

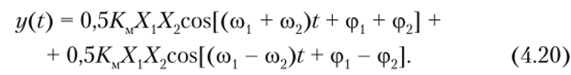
Из соотношений (4.19) и (4.20) следует важное свойство отклика: если амплитуда X_n(t), частота (c)"(?)> фаза Ф"(0 колебаний (4.19) является функцией времени, то отклик (4.20) сохраняет законы их изменения. Это свойство отклика предопределило широкое применение ПАС для построения различных узлов радиоэлектронной аппаратуры: преобразователей частоты, различных типов модуляторов и детекторов, синтезаторов частот и др. При этом полезным продуктом может быть как одна спектральная составляющая, так и обе, например:

• • в преобразователях частоты супергетеродинного приемника полезным продуктом в отклике (4.20) является только одна составляющая, а именно, составляющая с промежуточной частотой со_п = = |со, — со₂|, остальные составляющие должны быть подавлены (см. параграф 4.4);
• • в амплитудном и частотном модуляторах (см. параграф 4.5) используются обе составляющие.

Выделим и рассмотрим три способа перемножения аналоговых сигналов: идеальное перемножение, перемножение на НЭ и параметрическое перемножение.

Идеальное перемножение сигналов. Этот способ подразумевает перемножение в соответствии с выражением (4.18), т. е. без побочных продуктов в спектре выходного сигнала. Он базируется на использовании экспоненциальной зависимости тока р-п-переходов от приложенного напряжения:

где /₀ — обратный ток насыщения; U_T— температурный потенциал.

Перемножение осуществляется с помощью трех операций по следующему алгоритму (рис. 4.22, а).

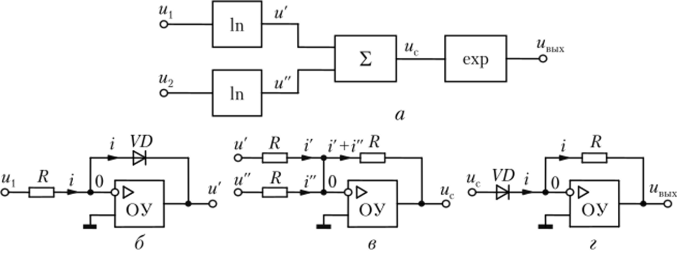
Рис. 4.22. Структура неремножителя аналоговых сигналов (а) и реализация операций логарифмирования (б), суммирования (в) и антилогарифмирования (г)

Шаг 1. Логарифмирование исходных напряжений г/, и и₂:

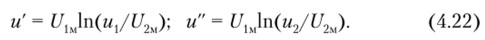
Я/яг 2. Сложение результатов логарифмирования:

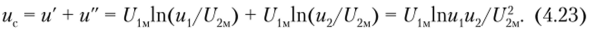
Шаг 3. Антилогарифмирование суммы напряжений:

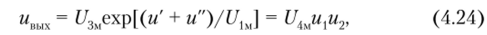
где U_iM, U_2m, U_3u, и_Лм — масштабирующие коэффициенты.

На рис. 4.22, б — г приведены схемы реализации математических операций, построенные на транзисторах и операционных усилителях. Чтобы доказать их правомерность, будем полагать, что ОУ обладает идеальными свойствами, а именно:

• • разность напряжения на его входных выводах близка к нулю, поэтому примем напряжение на инвертирующих выводах ОУ всех рассматриваемых схем равным нулю (виртуальный нуль);
• • входное сопротивление О У бесконечно велико, поэтому входной ток протекает на выход схемы через элемент обратной связи, мин’я ОУ.

С учетом принятых допущений:

• для схемы на рис. 4.22, б справедливо соотношение i = и JR = = I₀exp (-u'/U_T), откуда после логарифмирования получаем.

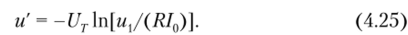
Аналогичным образом формируется напряжение и" ;

• в схеме на рис. 4.22, в суммарный ток i + i = (и + u)/R = -u_c/R, откуда с учетом соотношений (4.23) и (4.25) получаем.

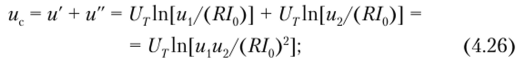
• уравнение для схемы на рис. 4.22, г имеет вид /₀ехр (м_с/Я_г) = = -u_Bblx/R, откуда с учетом соотношений (4.24) и (4.26) находим.

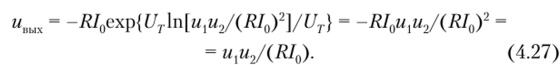
Сопоставляя (4.22) и (4.25), (4.23) и (4.26), (4.24) и (4.27), убеждаемся, что приведенные на рис. 4.22, б —г схемы с точностью до знака выполняют операции логарифмирования, суммирования и антилогарифмировапия.

Следует отметить, что при использовании полупроводниковых диодов диапазон рабочих напряжений ограничен двумя факторами:

• при больших прямых токах па омическом сопротивлении диода происходит значительное падение напряжения, что приводит к искажению характеристики (4.21);

• для диода U_T = шф_л где т = 1^-2, ср₇.~ 25 мВ. Корректирующий множитель т зависит от тока, поэтому удовлетворительная точность в схеме с диодом достигается только при изменении входного напряжения не более чем на два порядка. Применение транзисторов устраняет неблагоприятное влияние корректирующего множителя т и позволяет сохранить экспоненциальную форму характеристки (4.21) в пределах девяти декад.

Перемножение сигналов на НЭ. Этот способ находит широкое применение при построении функциональных узлов радиоэлектронной аппаратуры и имеет различные схемные реализации. Наилучшей характеристикой НЭ, описывающей зависимость отклика у от воздействующих колебаний х, является квадратичная функция у = Ах², поскольку при воздействии на НЭ с такой характеристикой суммы двух колебаний получаем отклик.

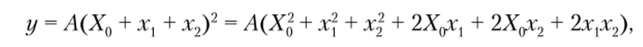
содержащий помимо полезного результата перемножения (2Ах₁х._}) минимальное количество побочных продуктов (АХ1, Ах, Ах.;, 2X₀x_v 2Х₀х₂), где А = const; Х₀ — смещение.

Характеристики реальных НЭ могут быть представлены степенным рядом.

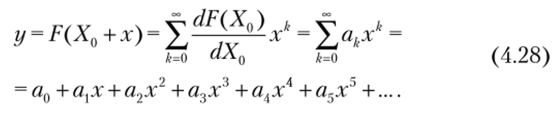
В этом случае отклик НЭ содержит составляющие вида С_тпх™х₂, где С_тп = const; т, п = 0, 1, 2,…, т. е. помимо полезного продукта перемножения двух сигналов С_их₁х₂ в отклике присутствует большое количество побочных составляющих. Учитывая соотношение (4.19), члены С_тпх™х₂ создают составляющие с полным набором комбинационных частот mw_l ± жо₂|. Для снижения их уровня принимают следующие меры:

• • уменьшают амплитуды X_v Х₂ перемножаемых сигналов, чтобы устранить влияние членов характеристики (4.28) со степенями х выше второй;
• • на выходе перемножителя включают фильтры, если требуется выделить только спектральную составляющую с требуемой частотой, например составляющую с разностной или суммарной частотой (4.20) перемножаемых сигналов;
• • используют несколько (два, четыре) НЭ для компенсационного (фазового) способа подавления побочных продуктов перемножения. Компенсационный способ позволяет смягчить требования к фильтрам (или вообще исключить фильтр), поэтому представляет интерес выявить его потенциальные возможности.

Компенсационный способ подавления побочных составляющих. Рассмотрим четыре идентичных НЭ с характеристикой (4.28) при воздействии на них четырех сигналов.

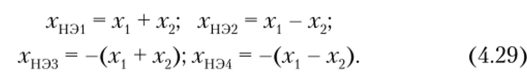
Подставив равенства (4.29) в ряд (4.28), получим следующие выражения откликов НЭ:

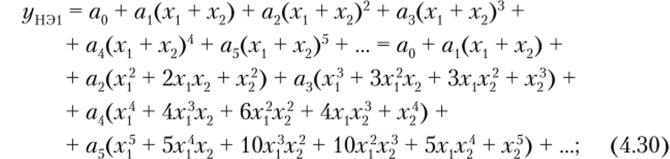
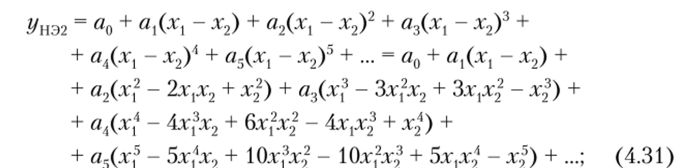
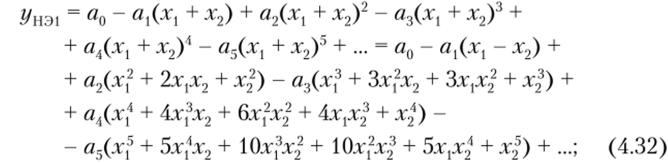
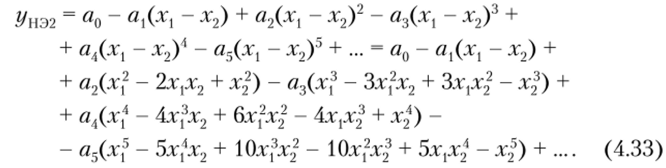
После подстановки равенств (4.19) в ряды (4.30) — (4.33) можно определить спектральный состав откликов, каждый из которых содержит полный набор комбинационных частот |тсо, ± то₂|, где т, п = = 0, 1, 2, 3,… Этот случай соответствует однотактным смесителям. Путем сложения и вычитания откликов НЭ количество спектральных составляющих в результирующем отклике может быть уменьшено, что облегчит выделение (фильтрацию) составляющей с преобразованной частотой со, + со._; или |со, — со._;|.

Составим суммы и разности откликов, содержащие произведение х_хх₂> которое позволяет получить полезный продукт преобразования с частотой |со, ± со₂|:

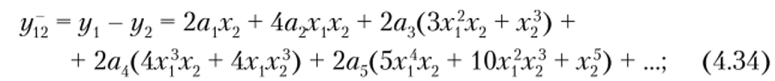
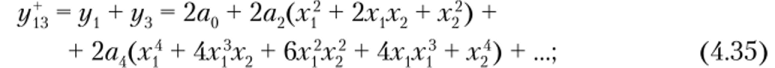
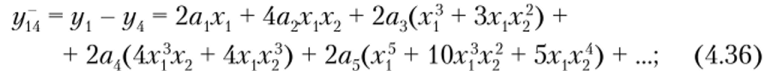
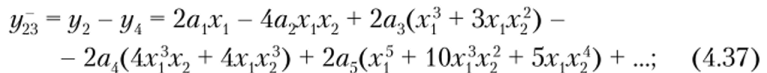
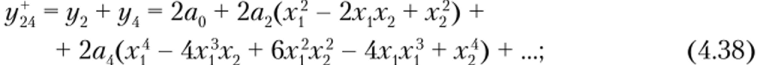
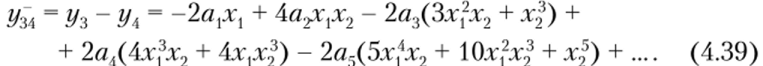
После подстановки равенств (4.19) в выражения (4.34) —(4.39) можно определить спектральный состав сумм и разностей откликов.

Разности откликов у_х2 (4.34) и у^ (4.39) содержат составляющие с частотами со₂, со, ± со₂, 2со, ± со₂, Зсо₂, 3c0j ± со₂, со, ± Зсо₂, 4со, ± со₂, 2со, ± Зсо₂, 5со₂, 5со, ± со₂, Зсо, ± Зсо₂, со, ± 5со₂,… Спектральный состав можно представить в общем виде: | /тгео, ± (2п + 1) со₂|, где т, п = 0, 1, 2,… В отличие от воздействия на НЭ только одного из колебаний (4.29) в спектре отсутствуют четные гармоники частоты со._;.

Разности откликов у_ХА (4.36) и у₂₃ (4.37) содержат составляющие с частотами со, со, ± со₂, Зсо, со, ± 2со₂, Зсо, ± со₂, со, ± Зсо₂, 5со, Зсо, ± 2со₂, со, ± 4со₉, 5со, ± со₂, Зсо, ± Зсо₂, со, ± 5со₉, 5со, ± 2со₉, Зсо, ± 4со." со, ± 6со₂,… или в общем виде |(2т + 1) со, ± жо₂|, где т, п = 0, 1,2,… В отличие от воздействия на НЭ только одного из колебаний (4.29) в спектре отсутствуют четные гармоники частоты со,.

Соотношениями (4.35) и (4.38) описываются отклики НЭ с характеристикой в виде четной функции при воздействии суммы и разности двух колебаний с разными частотами. Спектральный состав отклика может быть представлен выражением |(2т — п)со, ± ясо₂|, где т = 0, 1, 2,…; п = 0, 1, 2,…, 2 т.

Соотношения (4.34) и (4.39) отличаются лишь тем, что коэффициенты a_v а_л, а_5У … имеют разные знаки, поэтому члены с такими коэффициентами можно исключить путем суммирования этих соотношений: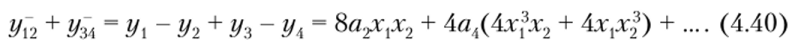

Выражения (4.36) и (4.37) отличаются тем, что коэффициенты a_v а_ъ, а… имеют одинаковые знаки, поэтому члены с такими коэффициентами можно исключить путем вычитания первого из этих выражений из второго: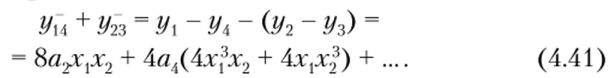

Путем вычитания отклика (4.38) из отклика (4.35) также можно исключить ряд членов:

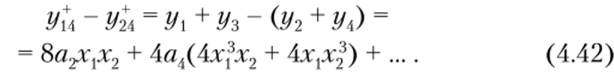
Соотношения (4.34)—(4.39) свидетельствуют о том, что результирующий отклик может быть получен тремя различными, но равноценными способами (4.40), (4.41) и (4.42). Спектральный состав отклика определяется после подстановки равенств (4.19) в соотношение (4.40), (4.41) или (4.42) и описывается следующим выражением: |(2т + 1) со₁ ± (2п + 1) со₂|. Спектр имеет минимальное число комбинационных частот в виде алгебраической суммы нечетных гармоник.

Схемная реализация компенсационного способа. Соотношения (4.34) — (4.39) описывают шесть возможных способов схемной реализации обычных балансных смесителей, которые показаны на рис. 4.23 для случая, когда в качестве НЭ используются иолупровод;

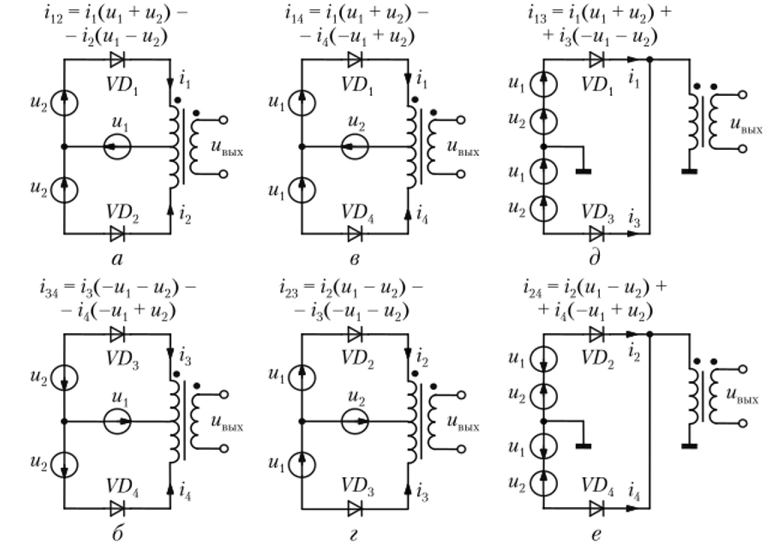
Рис. 4.23. Схемная реализация компенсационного способа подавления побочных продуктов преобразования частоты никовые диоды, при этом воздействиями являются напряжения, а откликами — токи. Отметим, что схемы на рис. 4.23, а и в, б и г отличаются лишь способом включения источников напряжения.

Используя схемы, изображенные на рис. 4.23, и соотношения (4.40) —(4.41), можно построить двойные балансные смесители. Для этого достаточно соединить вторичные обмотки трансформаторов в схемах на рис. 4.23, а и б последовательно согласно, а в схемах рис. 4.23, в и г, д и е — последовательно встречно. Однако такие схемные решения требуют большого количества трансформаторов. Поэтому на практике используется кольцевая схема смесителя, в которой диоды образуют замкнутый контур (кольцо).

На рис. 4.24, а показан принцип построения кольцевой схемы на основе схем балансных смесителей, приведенных на рис. 4.23, а и б. Нетрудно убедиться в том, что в кольцевой схеме направления воздействующих на полупроводниковые диоды напряжения и протекающих через первичные полуобмотки w' и w" токов такие же, как и в балансных схемах. Практический вариант кольцевой схемы приведен на рис. 4.24, б. В интегральной схемотехнике широкое применение находят балансные схемы на транзисторах.

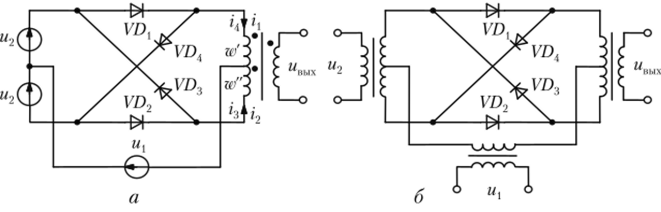
Рис. 4.24. Схемы кольцевого смесителя:

а — схема, поясняющая принцип его построения; б — практическая схема.