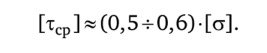Диаграмма растяжения. 
Основы функционирования систем сервиса. В 2 ч. Часть 1

Основной задачей испытаний на растяжение и сжатие является построение диаграмм растяжения и сжатия, которые отражают зависимость удлинения Д/ от нагрузки Р. На рис. 9.6, а приведена диаграмма для малоуглеродистой стали. Диаграмма имеет ряд характерных точек.

На участке ОА диаграмма прямолинейна — растяжение происходит с соблюдением закона Гука. При дальнейшем увеличении нагрузки прямая пропорциональность между Р и М нарушается, но образец сохраняет упругие свойства вплоть до точки К. За этой точкой возникают уже заметные остаточные деформации. Начиная с точки С до точки D удлинение образца происходит без увеличения внешней нагрузки. Образец, как говорят, «течет». Во время течения происходит перестройка кристаллических решеток материала образца и материал становится более прочным. Участок CD называется площадкой текучести.

В дальнейшем для увеличения удлинения ДI необходимо увеличить внешнюю силу Р. Однако при этом соотношение между Р и Д/ закону Гука не подчиняется. При достижении на диаграмме точки В на образце образуется так называемая «шейка» — местное уменьшение сечения (рис. 9.7). Шейка быстро развивается. При этом значение внешней нагрузки уменьшается, хотя напряжение растет, и в точке Е наступает разрыв образца.

Диаграмму растяжения обычно перестраивают в более удобной системе координат о_х и е_х (рис. 9.6, б). Форма диаграммы при этом не изменяется.

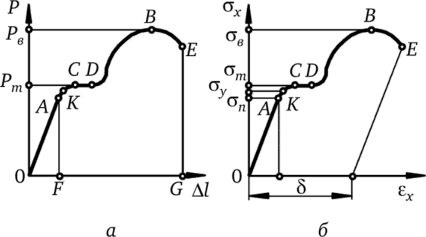
Рис. 9.6. Диаграммы растяжения образца из малоуглеродистой стали.

Рис. 9.7. Образование шейки при растяжении образца.

Наибольшее напряжение, до которого материал следует закону Гука, называется пределом пропорциональности а_пц. Пределом упругости а_у называется наибольшее напряжение, до которого материал не получает заметных остаточных деформаций. Предел текучести а_т — напряжение, при котором происходит рост деформаций без заметного увеличения нагрузки Р_т. Предел прочности а_в — отношение максимальной силы Р_в, которую способен выдержать образец, к его начальной площади поперечного сечения.

Сдвиг.

Касательные напряжения вызывают угловые деформации, так называемые сдвиги. Они характеризуются искажением прямого угла между двумя взаимно перпендикулярными волокнами, взятыми в деформированном теле.

Рассмотрим плоский элемент BCDE (рис. 9.8) упругого тела, находящегося под действием сил Р_ь Р₂, Р_п, который претерпел угловые деформации. Абсолютный сдвиг элементарного отрезка CD относительно отрезка BE, отстоящего от него на малом расстоянии h, будет СС_г = а.

Относительным сдвигом называется отношение a/h. Поскольку деформации весьма малы, то.

где у — угол сдвига.

Закон Гука при сдвиге.

Пусть на брус (рис. 9.9, а) с площадью поперечного сечения, А действуют сдвигающие силы Р. Воспользуемся методом сечений. Мысленно отбросим часть бруса, лежащую справа от сечения т—т (рис. 9.9, б). Действие отброшенной части на оставшуюся заменим силами интенсивности тху, действующими в сечении т—т (рис. 9.9, в). Равнодействующей этих сил является поперечная сила Qr Условие равновесия оставшейся части имеет вид.

Отсюда Р = Q_y. Поскольку можно считать, что касательные напряжения т_Ху направлены вертикально и по сечению распределяются равномерно, их значение

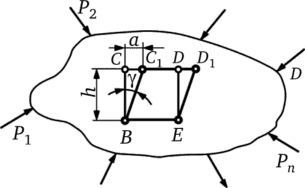
Рис. 9.8. Определение абсолютного и относительного сдвига элемента деформированного тела.

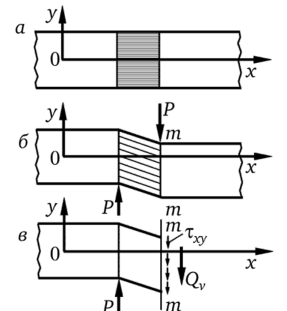
Рис. 9.9. Напряжение в брусе, испытывающем сдвиг.

Относительная деформация и напряжение при сдвиге связываются законом Гука:

где G — коэффициент пропорциональности, называемый модулем упругости второго рода (модулем сдвига).

В общем виде соотношение между модулем сдвига, модулем упругости первого рода и коэффициентом Пуассона выражается формулой.

Для стали G = 77—85 ГПа; для чугуна серого G = 45 ГПа (более подробные сведения даны в соответствующих справочниках).

Закон Гука при сдвиге, принимая во внимание выражения (9.12) и (9.15), можно записать в виде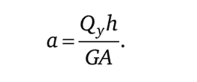

Произведение GA называют жесткостью бруса при сдвиге.

Формула прочности. При расчетах на срез формула прочности имеет вид.

где [т ] — допускаемое напряжение на срез, выбираемое чаще всего как часть допускаемого напряжения на растяжение: