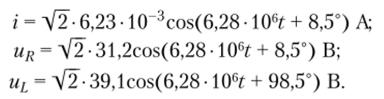Анализ простейших линейных цепей при гармоническом воздействии

Последовательная RL-цепь.

Рассмотрим идеализированную электрическую цепь, состоящую из последовательно включенных сопротивления R и индуктивности L (рис. 2.18, а). Пусть напряжение, приложенное к внешним зажимам цепи, изменяется, но гармоническому закону.

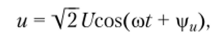
где U, со, f_u — заданные величины. Используя метод комплексных амплитуд, найдем установившееся значение тока i в цепи.

Искомый ток i является гармонической функцией времени той же частоты, что и приложенное напряжение:

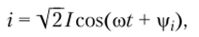
где /, ij — неизвестные действующее значение и начальная фаза тока Представляя сопротивление и индуктивность комплексными схемами замещения и переходя от тока i и напряжения и к их комплексным изображениям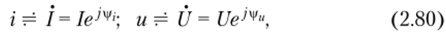

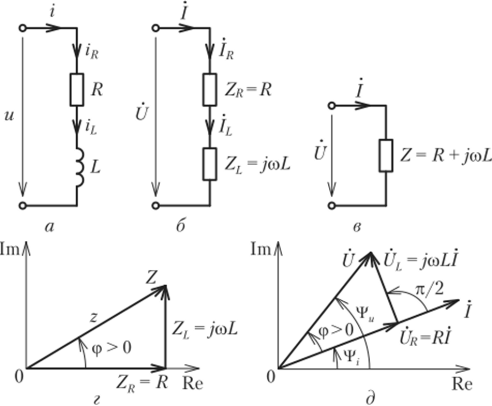
Рис. 2.18. Схемы и векторные диаграммы последовательной.

RL-ueim

получаем комплексную схему замещения цепи (рис. 2.18, б). Далее, используя законы Ома и Кирхгофа в комплексной форме, составляем систему уравнений электрического равновесия цепи:

где Z_R = R Z_L= jcoL — комплексные сопротивления входящих в рассматриваемую цепь идеализированных элементов.

Подставляя выражения (2.82)—(2.84) в уравнение (2.81), находим соотношение, связывающее комплексные изображения искомого тока и заданного напряжения:

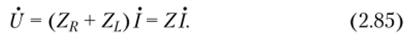
Выражение (2.85) представляет собой математическую запись закона Ома в комплексной форме для рассматриваемого участка цепи, причем Z = Z_R + Z_L= R + jcoL — комплексное входное сопротивление данного участка цепи. Выражению (2.85) можно поставить в соответствие комплексную схему замещения цепи (рис. 2.18, в). Таким образом, комплексное входное сопротивление цепи, состоящей из последовательно включенных сопротивления R и индуктивности I, равно сумме комплексных сопротивлений этих элементов. В дальнейшем мы убедимся (см. п. 2.6), что аналогично можно найти комплексное сопротивление любого участка цепи, представляющего собой последовательное соединение произвольного числа идеачизированных двухполюсных элементов.

Комплексное входное сопротивление рассматриваемой цепи может быть изображено на комплексной плоскости в виде вектора Z, равного геометрической сумме векторов Z_R и Z_L (рис. 2.18, г). Длина этого вектора равна, в выбранном масштабе, модулю комплексного входного сопротивления цепи.

а угол наклона к положительной вещественной полуоси — его аргументу.

Очевидно, что при конечных значениях со, L и R угол (р лежит в пределах.

Когда аргумент комплексного входного сопротивления (р какого-либо двухполюсника равен нулю, то говорят, что его входные сопротивление и проводимость имеют чисто резистивный (вещественный) характер, когда |ф | = к/2, то входные сопротивление и проводимость имеют чисто реактивный (мнимый) характер. Если аргумент комплексного входного сопротивления двухполюсника равен +л/2, то его входные сопротивление и проводимость имеют индуктивный характер, если к = -п/2 — емкостный. В рассматриваемом случае значение аргумента ф определяется соотношением (2.88), поэтому входное сопротивление цепи имеетрезистивно-индуктивный характер.

Используя соотношение (2.85), находим комплексное действующее значение искомого тока: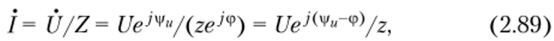

где 2 и ф определяются соотношениями (2.86) и (2.87). Из выражений (2.89) и (2.80) можно найти действующее значение и начальную фазу тока:

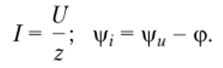
Переходя от комплексного изображения тока к оригиналу, окончательно получаем.

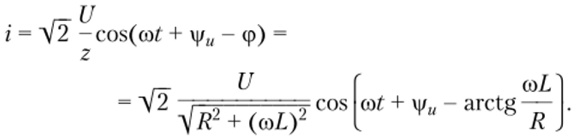
В связи с тем, что при заданной частоте внешнего воздействия со установившиеся значения токов и напряжений цепи полностью определяются их действующими значениями и начальными фазами, на практике обычно не возникает необходимости находить оригиналы токов и напряжений. Решение задачи анализа цепи считается законченным, если получены комплексные действующие значения соответствующих функций.

Векторные диаграммы для тока и напряжений /?1-цепи приведены на рис. 2.18, д. Так как напряжение на сопротивлении совпадает ио фазе с током, вектор U_R совпадает по направлению с вектором /, вектор (] повернут относительно вектора / на угол л/2 против часовой стрелки (напряжение на индуктивности по фазе опережает ток на я/2). Независимо от начальной фазы напряжения у, вектор / повернут относительно вектора 0= U_!{ + U_L по часовой стрелке на угол ф, т. е. ток отстает ио фазе от напряжения на угол ф, равный аргументу комплексного входного сопротивления цепи. Отметим также, что так называемый треугольник напряжений, образованный векторами U, U_R и U_L (см. рис. 2.18, д), подобен треугольнику сопротивлений (см. рис. 2.18, г), образованному векторами Z, Z_R и Zj.

Из векторной диаграммы очевидно, что действующие значения напряжения на входе цепи U, напряжения на сопротивлении U_R и напряжения на индуктивности U_L, которые определяют длину сторон треугольника напряжений, связаны соотношением.

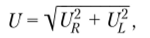
т.е. действующее значение напряжения па входе цени не равно алгебраической сумме действующих значений напряжений на элементах цепи.

Пример 2.3. Найдем комплексное входное сопротивление и ток последовательной Л'/.-цени (смлшс. 2.18, а), к зажимам которой приложено напряжение и = V2 • 50cos (6,28 • 10⁶f + 60°) В. Определим напряжения на элементах цепи (R = 5 кОм; L = 1 мГн).

Комплексное входное сопротивление Z последовательной RL-цепи равно сумме комплексных сопротивлений входящих в нее элементов:

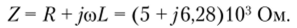
Переходя от алгебраической формы записи к показательной.

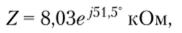
находим модуль комплексного входного сопротивления Z = = 8,03 кОм и его аргумент ф = 51,5°. Комплексный ток цепи.

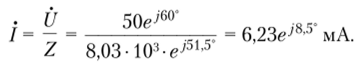
Комплексные напряжения на сопротивлении и индуктивности:

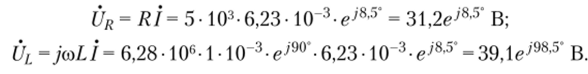
Мгновенные значения соответствующих величин: