Экономика возобновляемых и невозобновляемых ресурсов

Рынки капитала тесным образом связаны с вложениями в добычу полезных ископаемых и другие природные ресурсы. Природные ресурсы и некоторые продукты их первичной переработки (древесина, крупный рогатый скот, вино) имеют тенденцию увеличиваться с возрастом в цене, хотя и с уменьшающейся скоростью. Типичный график стоимости подобных факторов производства (V) представлен на рис. 19.7.

Природные ресурсы подразделяются на возобновляемые и невозобновляемые. Возобновляемые природные ресурсы обладают внутренней возможностью воспроизводства, самостоятельно или при участии человека. Деревья могут быть посажены на месте вырубок леса. Поголовье скота может быть увеличено за счет естественного прироста. Виноградники могут быть дополнительно культивированы в пригодных для этого местностях.

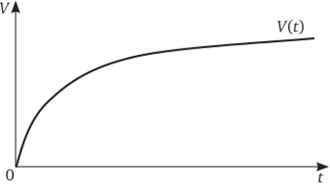
Рис. 19.7. Изменение стоимости природных ресурсов с течением времени.

Невозобновляемые ресурсы не восстанавливаются. Человечество обладает определенным запасом полезных ископаемых (нефть, уголь, бокситы), металлов и некоторых других ресурсов, воссоздать которые не представляется возможным. Для таких факторов производства известна конечная точка — запас ресурса обязательно закончится, хотя и необязательно в самом ближайшем будущем.

Невозобновляемые ресурсы ставят перед экономистами очень важную проблему. Какой объем ресурса следует добывать и продавать сегодня, в данный период времени, а какой — целесообразнее отложить на будущее (законсервировать)?

Предположим, что предельные издержки добычи невозобновляемого ресурса равны нулю. Сегодняшняя цена на ресурс составляет Р_г Отложить добычу фактора производства на один год имеет смысл тогда, когда дисконтированная стоимость завтрашних поступлений от продажи ресурса ока;

р

жется выше текущей цены: j¹¹³— > P_t.

Но к такому выводу могут прийти все участники рынка. Однако чем меньше добывается ресурса сегодня, тем больше будет добыто завтра (ресурс исчерпаем). Это увеличивает сегодняшнюю цену и снижает завтрашнюю. Если рынок ресурса конкурентен, то в равновесии: P_t+1 = (1 + i) P_t, будущая стоимость ресурса зависит от альтернативных возможностей использования денег: деньги могут быть затрачены на добычу полезного ископаемого или могут быть помещены в банк под процент i.

Здесь проявляется закон Хотеллинга: цена ресурса возрастает от периода к периоду в соответствии со ставкой процента.

Историческая справка.

Гарольд Хотеллинг (1895—1973), американский экономист и статистик. В университете Вашингтона получил степень бакалавра по журналистике и магистра по математике. Окончил аспирантуру Принстонского университета. Преподавал в Стэнфордском и Колумбийском университетах, где возглавлял кафедру экономики. В 1936—1937 гг. был президентом Эконометрического общества США.

С 1946 г. возглавлял департамент статистики в университете Северной Каролины. Основные работы посвящены математической теории амортизации, экономике исчерпаемых ресурсов, теории общего благосостояния и налогообложения, анализу функции спроса. Г. Хотеллинг является автором модели линейного города, используемой при исследовании поведения фирм на рынках с дифференцированным продуктом.

Для монопольного рынка невозобновляемых ресурсов равновесие окажется там, где наблюдается равенство межвременной предельной доходности (предельной выручки):

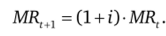
Так как P_t > MR_t, то q_tK > q,", монополист будет добывать меньше сегодня и больше завтра по сравнению с конкурентной отраслью. Цена добываемого ресурса будет первоначально выше в монопольной отрасли (согласно оптимуму монополиста), а затем будет снижаться.

Для возобновляемых ресурсов ставка процента также играет существенную роль.

Производство возобновляемых ресурсов, как правило, характеризуется наличием точки производственного максимума (рис. 19.8). Если Y (t) — производственная функция использования ресурса, то точка Е, показывает максимальный физический объем ресурса, который может быть получен при данных условиях. Это может быть наивысшая отдача от участка леса, наилучшее качество выдержанного вина, наибольший улов рыбы в озере или с определенной площади моря.

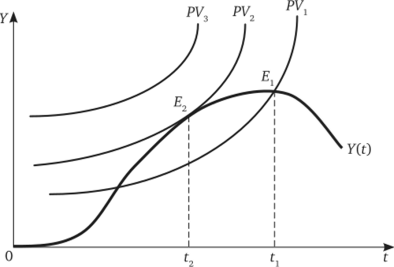
Рис. 19.8. Оптимальный срок использования возобновляемого ресурса.

Должна ли фирма использовать ресурс в момент времени t_v соответствующий его максимальной физической продуктивности? Как правило, нет.

Для компании имеет значение совокупная возможная межвременная стоимость ресурса. Она определяется как дисконтированная совокупная доходность ресурса:

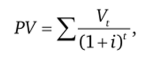
где V, = Р_г? Y (t) — текущая стоимость ресурса в момент времени t; i — ставка процента.

В зависимости от показателей i, 7(t), Р, дисконтированная доходность ресурса может быть различной. При фиксированных параметрах мы получаем линии одинаковой дисконтированной доходности как геометрическое место функции PV = PV (t). На рис. 19.8 представлены три линии дисконтированной доходности (аналог кривой безразличия).

Фирма стремится максимизировать функцию дисконтированной доходности при ограничении со стороны производственной функции 7(f). Оптимальный срок использования ресурса определяется точкой касания производственной функции ресурса и линии его дисконтированной доходности — это точка Е₂, которая в силу соответствующей формы как производственной функции, так и линии дисконтированной доходности, находится левее точки Е, — точки максимума физической доходности ресурса. Таким образом, оптимальное время использования ресурса будет меньше его физической «зрелости»: t₂ < t_r

Так как природные ресурсы изменяются непрерывно (деревья растут каждый день, вино выдерживается каждый день), для анализа оптимального времени можно воспользоваться методом непрерывного начисления сложных процентов.

Если процент в банке выплачивается N раз в год, то при ставке процентов г через t лет вкладчик получает сумму: (l + i/JV)'^vt. Каков предел этого выражения при N —> оо? Данный предел находится по формуле: е" = lim (l + i/N)^№.

Дисконтированная доходность ресурса теперь составит.

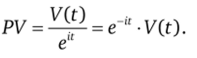
Найдем максимум данной функции по отношению к времени. Для этого вычислим условие первого порядка.

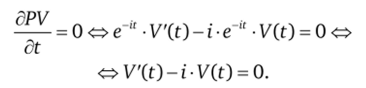
Откуда получаем.

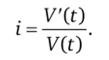
Оптимальное время использования ресурса должно удовлетворять условию равенства ставки процента темпу прироста этого ресурса.

Задача, иллюстрирующая теорию

Чем больше срок выдержки рома, тем больше его стоимость. Известно, что если принять стоимость рома в первый период за 1, то в период t его стоимость будет составлять: V (t) = е'¹'" ⁰¹'. Если рыночная ставка процента равна 10%, в каком году следует продать ром для максимизации прибыли фирмы? Как изменится срок продажи рома, если ставка процента упадет до 5 или возрастет до 15%?

Решение

В данной задаче необходимо найти максимальную разницу между дисконтированной стоимостью и инвестициями в начальный период.

Дисконтированная стоимость вычисляется по формуле: PVD = ———. Эта формула показывает ценность будущего дохода сегодня, так как доход, равный: _еД-°, п, _в пер_ИОДе f можно получить, положив в банк сегодня сумму, равную:

_еЛ-0,!г.

—-при ставке процента г. В любом периоде t общий доход от продажи бутылки рома за все периоды от 0 до t равен значению функции: V® = _e ^f ^^01f, поскольку бутылка рома продается один раз в данном периоде.

gji-0.ll.

Тогда чистая дисконтированная стоимость составит: NPV = ——— -/ (где/ —.

инвестиции в начальный период). В данном случае поскольку стоимость бутылки рома равна 1 в начальный период, то инвестиции, необходимые в начальный период, равны стоимости бутылки рома в начальный период и составляют 1.

gji-0.lt.

Зная ставку процента г = 10%, найдем: NPV = ^ -1.

Для поиска максимума вычислим условие первого порядка: dNPV/dt = 0.

Откуда получаем результат: t = 6,55; V (6,55) = 2,6; NPV (6,55) = 2,6 — 1 = 1,6. Таким образом, бутылку рома необходимо продать через 6,55 лет, чтобы макси;

gji-0.lt.

мизировать NPV и, следовательно, эффективность и прибыль. Величина —-;

есть выручка фирмы за период от 0 до t, измеренная в сегодняшней ценности, а I = 1 — общие затраты фирмы.

gJi-0.lt.

Если ставка процента повышается до г = 15%, то: NPV ——-1 и, макси;

^ (1+0,15)'.

мизируя эту функцию, найдем, что t = 4,35; V (4,35) = 1,84 и NPV = 1,84 — 1 = 0,84.

gji-0.lt.

Если ставка процента снизится до г = 5%, то NPV =——1; итоговые резуль;

^к (1 + 0.05)' ^у

таты составят t= 11,29; У (11,29) =4,37; NPV= 4,37 — 1 = 3,37.

Прибыль фирмы зависит обратно пропорционально от ставки процента. Выражение (1 + г)' находится в знаменателе, следовательно, чем выше г, тем ниже дисконтированная стоимость. Это объясняется следующим: чем выше ставка процента, тем дешевле деньги будущего периода, выраженные в деньгах настоящего периода, увеличение ставки процента означает увеличение альтернативных издержек инвестирования.