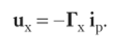Топологические матрицы и их использование для описания цепей

Под топологической структурой, или топологией, электрической цени обычно понимается ее конфигурация, определяемая способом соединения базисных компонентов двухполюсников, при этом тип компонентов не играет никакой роли. Полное описание цепи включает два вида уравнений:

• • топологические уравнения, характеризующие структурные особенности цепи, или ее конфигурацию. Для их составления используются граф цепи и топологические матрицы;
• • компонентные уравнения, отражающие характеристики компонентов (ветвей).

Для топологического описания свойств цепи широко используется одно из направлений математики — теория графов.

Основные понятия теории графов. Топологическое описание цепи должно содержать:

• • способ соединения ветвей;
• • опорные направления для токов ветвей и напряжений.

Для описания способа соединения ветвей цепи используется ненаправленный граф, представляющий собой совокупность отрезков произвольной длины и формы, называемых ветвями (ребрами), и точек их соединения (или окончаний), называемых узлами (вершинами). Для перехода от схемы электрической цепи (рис. 4.6.1, а) к ненаправленному графу (рис. 4.6.1, б) следует заменить элементы (двухполюсники) ветвями графа.

Опорные направления тока и напряжения помечаются на ветвях графа стрелками. Стрелка направлена от вершины графа, соответствующей полюсу цепи с положительным потенциалом, и указывает положительное направление тока.

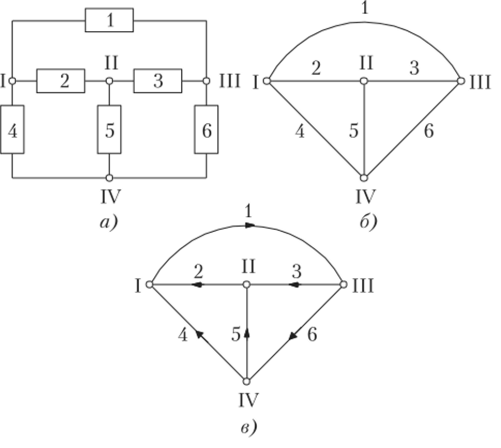
Рис. 4.6.1. Электрическая цепь (а) и ее представление в виде ненаправленного (б) и направленного (в) графов через ветвь. Такой принцип разметки исключает необходимость использования отдельных наборов опорных точек для токов и для напряжений. Граф с ориентированными ветвями называется направленным графом (рис. 4.6.1, в). Он содержит полную информацию о топологии цепи.

Для пояснения ряда понятий будем использовать приведенные на рис. 4.6.1 схему и оба вида графов, при этом ветви графа обозначены арабскими цифрами, узлы — римскими.

Помимо ненаправленного и направленного графов известно большое количество других видов графов. Среди них следует выделить:

• • непланарный (пространственный) граф с пересекающимися (1 и 2) ветвями (рис. 4.6.2, а), если при его изображении на плоском чертеже невозможно избежать пересечения ветвей, и планарный (плоский) граф, который можно изобразить на плоскости без пересечения ветвей (рис. 4.6.2, б);
• • подграф (рис. 4.6.2, в), представляющий собой любую совокупность ветвей и вершин основного графа (см. рис. 4.6.2, б);
• • связный граф (см. рис. 4.6.2, б), в котором имеется хотя бы один путь между любой парой узлов, и несвязный граф в противном случае (см. рис. 4.6.2, в);

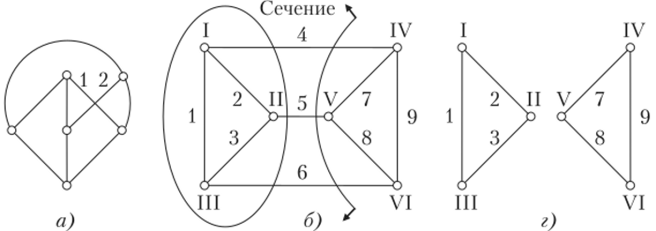
Рис. 4.6.2. Непланарный граф (я), планарный граф (б) и его подграфы (в).

• • путь графа — подграф в виде непрерывной последовательности ветвей (1—3—5—8—9 на рис. 4.6.2, б), связывающей пару выбранных узлов (I, IV), с прохождением каждого узла не более одного раза;
• • контур — связный подграф, имеющий замкнутый путь, в котором начальная вершина совпадает с конечной. В контуре к каждому узлу присоединены по две ветви. На рис. 4.6.3 изображены все семь контуров ненаправленного графа на рис. 4.6.1, б;
• • сечение — любая минимальная совокупность ветвей (4, 5, 6 на рис. 4.6.2, б), при удалении которых граф распадается на два несвязных подграфа (см. рис. 4.6.2, в). Восстановление любой ветви из удаленного набора приводит к связному графу. Отметим, что количество ветвей в сечении не фиксировано. В частном случае несвязный подграф может не иметь ветвей и состоять только из одного узла. Число возможных сечений может намного превысить число узлов. Сечение изображается линией, однократно пересекающей каждую его ветвь. Для изображения будем использовать овал или линию со стрелками (см. рис. 4.6.2, б), указывающими на внутреннюю область сечения, которую называют обобщенным узлом. Введение этого понятия позволяет однозначно задать направление токов: втекающих в узел, вытекающих из узла.

Таким образом, в общем случае сечение разделяет цепь на две части, связанные друг с другом с помощью соединительных ветвей. Для любого сечения выполняется второй закон Кирхгофа: алгебраическая сумма токов, протекающих по соединительным ветвям сечения, равна нулю;

• дерево графа, представляющее собой связный подграф, который содержит все узлы исходного связного.

Рис. 4.63. Полный набор контуров ненаправленного графа.

на рис. 4.6.1, б графа и не содержит контуров. Между любой парой узлов дерева имеется единственный путь. Ветви, принадлежащие дереву, будем называть ребрами, а ветви, не принадлежащие дереву, — хордами. Все хорды, соответствующие данному дереву, образуют подграф, называемый дополнением дерева. На рис. 4.6.4, а приведено дерево для графа на рис. 4.6.1,6, при этом ребра нанесены сплошными линиями, а хорды — пунктирными. Число ребер: ЛГ_р = ЛГ_у— 1=4 -1=3; число хорд: Лх ⁼ Nj* - N_y + 1 = 6 — 4 + 1 = 3. Число возможных деревьев N._{ исходного графа очень быстро растет с увеличением числа узлов: для N_y = 4 имеем Л^г_д = 16 (рис. 4.6.5); для N_y = 6 — N_;{ = = 1296. С деревом связаны главные контуры и главные сечения, которые определяют ряд важных свойств графа;

• главное сечение, содержащее только одну ветвь дерева (ребро), которая не входит в другие сечения, и несколько хорд. Поэтому уравнения равновесия токов в главных сечениях являются независимыми. Для выбранного дерева число.

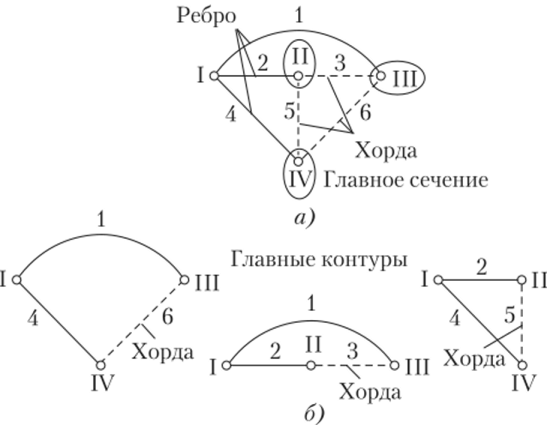
Рис. 4.6.4. Полный набор главных сечений (а) и главных контуров (б) ненаправленного графа на рис. 4.6.1, б.

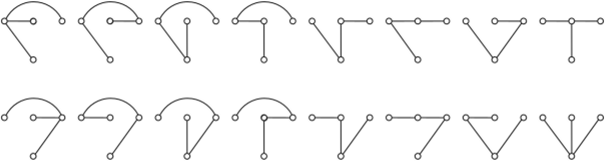
Рис. 4.6.5. Полный набор деревьев ненаправленного графа на рис. 4.6.1, б.

главных сечений равно числ}' его ребер N_p=N_y-1 = 4 -1 = 3 (см. рис. 4.6.4, а);

• главный контур, образующийся при подключении хорды к дереву графа (см. рис. 4.6.4,б). Уравнения равновесия напряжений в главных контурах являются независимыми. Для выбранного дерева число главных контуров равно числу его хорд: N_x = N_B — N_y + 1 = 6 — 4 + 1 = 3.

Топологические матрицы. Содержащаяся в направленном графе информация может быть полностью представлена топологическими матрицами, которые служат его аналитическим описанием. Топологические матрицы играют важную роль в теории цепей, так как позволяют:

• • автоматизировать процесс составления уравнений исследуемой цепи по законам Кирхгофа;
• • получить систему из линейно независимых уравнений, которая всегда имеет решение.

В общем случае для построения топологической матрицы предварительно следует:

• • составить (выбрать) дерево исходного графа;
• • пронумеровать узлы, ветви, главные сечения и главные контуры графа. При нумерации ветвей будем нумеровать сначала ребра, а затем — хорды. Ниже показано, что раздельная нумерация ребер и хорд позволяет выделить в топологической матрице единичную подматрицу. Номер главного сечения совпадает с номером входящего в его состав ребра, а номер главного контура — с номером хорды;
• • выбрать положительные направления ветвей графа. Этот выбор подчинен получению единичной подматрицы и обосновывается при рассмотрении конкретных матриц.

Проллюстрируем это на примере графа с N_y = 4 узлами и N_ls = 6 ветвями. На рис. 4.6.6, а изображено дерево графа, содержащее:

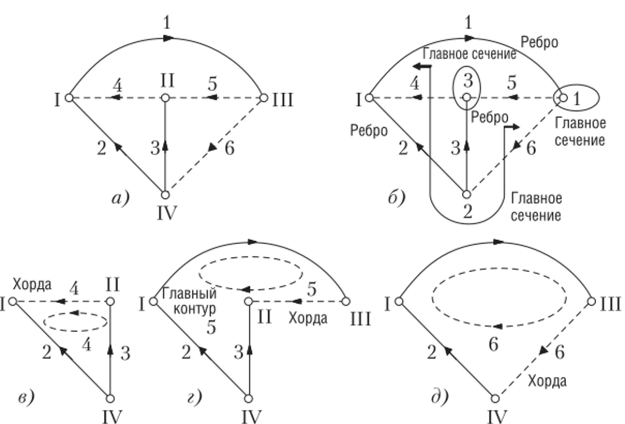
Рис. 4.6.6. Иллюстрация построения топологических матриц:

а — исходный граф; б — его главные сечения; в—д — его главные контуры.

три ребра (1, 2, 3) и три хорды (4, 5, 6);

• • три главных сечения (рис. 4.6.6, б), каждое из которых содержит только пересекаемые сечением ветви графа: сечение 1 содержит ребро 1 и хорды 5, 6; сечение 2 — ребро
• 2 и хорды 4, 6 (обратить внимание на разметку); сечение
• 3 — ребро 3 и хорды 4, 5. Номер каждого сечения совпадает с номером принадлежащего сечению ребра. Ток ребра каждого главного сечения направлен во внутрь сечения (обобщенного узла);
• • три главных контура 4, 5, 6 (рис. 4.6.6, в—д). Направление контурного тока совпадает с направлением тока входящей в контур хорды.

Матрица инциденций. Среди топологических матриц широко используется N_yxN_H матрица инциденций A_a=tfy, или соединений узел—ветвь. Каждая i-я строка такой матрицы показывает, какие ветви связаны с данным узлом, или, как говорят, инцидентны /-у узлу. Отсюда название матрицы. Для направленного графа (см. рис. 4.6.6, а) матрицу инциденций можно представить в виде табл. 4.6.1, строки которой являются порядковыми номерами узлов.

(г), а столбцы — номерами ветвей (/). Число строк полной матрицы А_а = [afj равно числу узлов графа (N_y = 4), а число столбцов — числу ветвей (N_B = 6).

Каждый элемент а_1} матрицы А_а равен:

• • +1, если j-я ветвь входит в i-и узел;
• • -1, если j-я ветвь выходит из i-го узла;
• • 0, если она не соединена с i-u узлом.

Отметим, что при определении элементов можно пользоваться разными правилами, лишь бы они были единообразными при определении знаков всех ненулевых элементов матрицы.

Таблица 4.6.1

Поскольку каждая ветвь соединена с двумя узлами, в один из которых она входит, а из другого выходит, то сумма элементов в каждом столбце, а значит, и сумма элементов всей таблицы равна нулю. Следовательно, любую строку можно рассматривать как линейную комбинацию остальных строк. Поэтому одну из строк, обычно соответствующую базисному узлу (например, узлу IV), вычеркивают. Образующаяся при этом редуцированная матрица, А размером (N_y — 1) ^ХЛГ_В называется матрицей узлов. Если каждой j-й ветви сопоставить ток ij (табл. 4.6.1), то закон Кирхгофа для токов в матричной форме имеет вид.

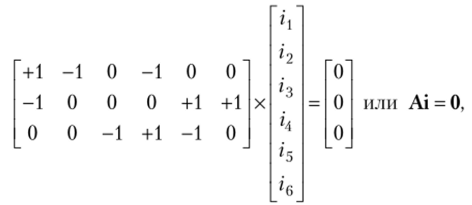
где i — вектор токов размерности N_B; 0 — нулевой вектор размерности N_y — 1.

Матрицу соединений, А можно представить в виде подматриц А_р и А_х, относящихся к ребрам и хордам (соответственно левая и правая часть табл. 4.6.1).

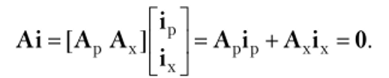
Матрица главных сечений. Каждое главное сечение включает в себя одно ребро и нескольких хорд. Число главных сечений равно числу ребер ЛГ_р. Поэтому уравнения равновесия токов в главных сечениях являются независимыми. На рис. 4.6.6, 6 показаны три главных сечения (1, 2, 3) выбранного дерева.

Матрицу главных сечений П можно представить в виде табл. 4.6.2 размером (N_y — 1) ^XN_U, i-я строка которой соответствуют главному сечению, a j-й столбец — ветви графа. Каждый элемент этой матрицы равен:

• • +1, если j-я ветвь выходит из /-го сечения;
• • -1, если j-я ветвь входит внутрь /-го сечения;
• • 0, если j-я ветвь нс содержится в сечении.

Таблица 4.6.2

Матрица П описывает соединения ветвей, входящих в независимые сечения. Ее можно представить в виде единичной матрицы 1 порядка N_? и подматрицы П_х порядка iV_p х N_x: П = [1 П_х]. Каждая i-я строка П_х показывает, какие хорды входят в главное сечение, образованное соответствующим ребром дерева, а j-й столбец — в какие сечения входит j-я хорда.

Элементы ау матрицы П являются коэффициентами уравнений, которые составляются для токов в главных сечениях и могут быть представлены в следующем виде:

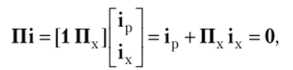
где.

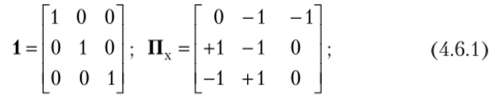
ip ⁼ h h У^т; К = [^г4 ^г5%]^т" ^т знак транспонирования матрицы, позволяющий для удобства записи столбец представить в виде строки.

В каждое уравнение системы входит единственный ток ребра, поэтому можно выразить токи ребер через токи хорд:

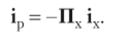
Матрица главных контуров. Каждый главный контур состоит из одной хорды, которая не входит в другие контуры, и нескольких ребер. Поэтому число главных контуров равно числу хорд N_x и уравнения равновесия напряжений в главных контурах являются независимыми. На рис. 4.6.7, в—д показаны три главных контура (4, 5, 6), соответствующих выбранному дереву.

Матрицу главных контуров Г можно представить в виде табл. 4.6.3 размером [N_B — (N_y — 1)] х JV_B, i-я строка которой соответствуют главному контуру, a j-й столбец — ветви графа. Каждый элемент а_}] этой матрицы равен:

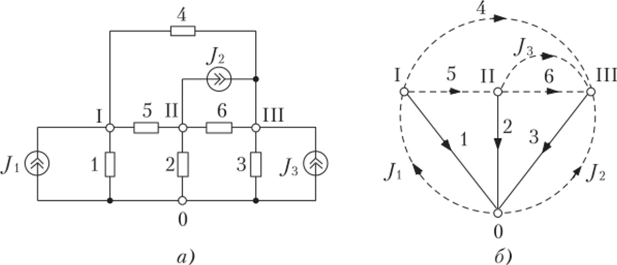
Рис. 4.6.7. Схема (а) и граф (б), используемые для иллюстрации составления уравнений узловых напряжений.

• • +1, если направление у-й ветви совпадает с направлением обхода контура;
• • -1, если направлениеу-й ветви не совпадает с направлением обхода контура;
• • 0, если ветвь не входит в главный контур.

Таблица 4.6.3

Матрицу Г можно разбить на две части: подматрицу Г_р порядка N_xxN_p, которая получается из матрицы главных контуров исключением всех хорд, и единичную матрицу порядка N_x: Г = [Г_р 1]. Каждая /'-я строка подматрицы Г_р показывает, какие ребра входят в главный контур, образованный замыканием соответствующей хорды, ау-й столбец — в какие контуры входит j-e ребро.

Элементы а^ матрицы Г являются коэффициентами уравнений, которые составляются, но закону Кирхгофа для напряжений в главных контурах и могут быть представлены в следующем виде:

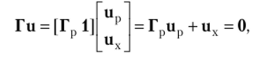
где.

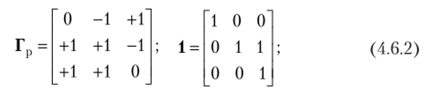
u_p = [u и₂ w₃]^T; и_х = [м₄ и_{5 и}г₆] ^т; т — знак транспонирования матрицы.

В каждое уравнение системы входит одно напряжение хорды Uj, поэтому с помощью матрицы Г_х напряжения хорд можно выразить через напряжения ребер: