Движение точки по прямой в сопротивляющейся среде. 
Метод фазовой плоскости

Прямолинейное движение материальной точки является простейшим типом движения материальной точки. Получим необходимые и достаточные условия прямолинейного движения свободной материальной точки. Пусть движение материальной точки относительно инерциальной системы координат прямолинейно, т. е. г (г) = г₀ + дг,(/)е|, где г₀, е₍(| е₃1 = 1) — постоянные векторы. Тогда F = /яг = тх, е, т. е. сила, действующая на точку, направлена по оси Ох| (е, — орт оси Ох_х). Уравнения движения в проекциях на оси Ох₂, СЬс₃ имеют вид тх₂ = 0, тх₃ = 0 и их решения х₂ = х₂(0) + + jc₂(0)r, х₃ = х₃(0) + х₃ (0)Л Достаточные условия прямолинейности движения представляются равенствами х₂(0) = х₃(0) = 0.

Рассмотрим несколько случаев прямолинейного движения вдоль оси Ох.

1. Движение под действием силы, зависящей от времени. Имеем.

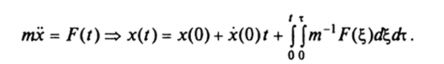
2. Движение под действием силы, зависящей от скорости. Имеем.

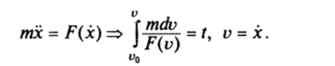
Обозначая через Ч'(о) первообразную функции m[E (i;)]'¹, получим Ч'(о) — 44i>o) = /, v = 'V- +'Y (vо)) и.

П. 1. Если F = -сх, с > 0 — сила сопротивления пропорциональна скорости, то.

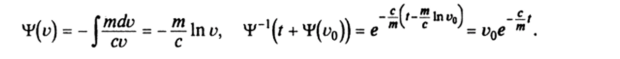
Закон движения точки Когда t стремится к бесконечности, x (t) стремится к х (0) + mc~'v₀.

П. 2. Пусть F= mgmcv² sign и — модель падения тела по вертикали с учетом сопротивления воздуха. Предположим, что в начальный момент времени х (0) = х (0) = 0. Тогда.

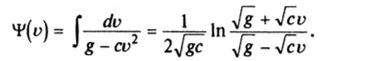
С учетом начальных условий равенство Ч^/(и)-Ч^>(0) = I, представляется в виде.

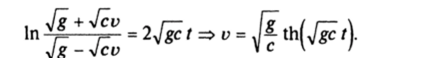
Ясно, что при t -* оо v (t) -> yjgc~*, т. е. тело будет падать с постоянной скоростью. Нетрудно найти и закон движения x (t).

3. Движение материальной точки под действием силы, зависящей от положения точки. Если сила F= F (x), то существует силовая функция U (x) и интеграл энергии.

• 0.5.1. Плоскость с координатами (х, х) называется фазовой плоскостью.
• 0.5.2. Однопараметрическое семейство кривых

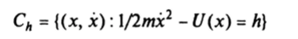
на фазовой плоскости называется фазовым портретом.

Множество См вообще говоря, есть объединение конечного или бесконечного числа фазовых траекторий. Начальные условия движения (х (0), х (0)) определяют односвязную компоненту множества C_h — фазовую траекторию, по которой в дальнейшем движется точка на фазовой плоскости. Закон движения материальной точки определяется из соотношений.

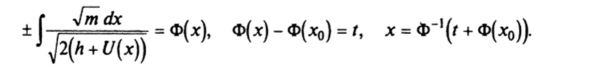
Отметим ряд свойств фазовых кривых:

• а) фазовая кривая симметрична относительно оси Ох (см. (5.1));
• б) через каждую точку фазовой плоскости проходит только одна фазовая кривая (теорема существования и единственности решений дифференциальных уравнений);
• в) точки с координатами (х_к, 0), где х* — корни уравнения dU (x)/dx= 0 (стационарные точки силовой функции), являются фазовыми кривыми и называются положениями равновесия;
• г) если точка (х, 0) не является положением равновесия, то через нее проходит фазовая траектория, касательная к которой в этой точке ортогональна оси Ох. Другими словами, фазовые траектории пересекают ось Ох в регулярных точках под прямым углом.

А Вычислим.

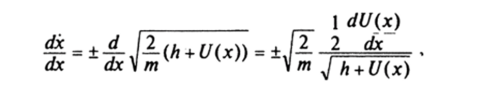
Числитель дроби отличен от нуля, а знаменатель равен скорости точки х = 0. ?

II. Пусть масса материальной точки т = 2, потенциальная энергия V=-U (x) = -cos х и точка движется по оси Ох. Уравнения движения и интеграл энергии представляются в виде.

Линии уровня полной энергии C_h = {(х, х):х = ±>/А + cosx} образуют фазовый портрет (рис. 16). Если h < -1, то множество C_h пусто. При A = -1 C_h = {х = 0, х = пк_у к eZ) — множество положений равновесия. Когда -1 пк, к eZ} и сепаратрис, их соединяющих. Движение по сепаратрисам называется лимитационным, а время движения по сепаратрисе к положению равновесия стремится к бесконечности. В самом деле, если выбрать сепаратрису в верхней полуплоскости и начать движение из точки х = 0, х = yf2, то

При х -> п время движения t -> оо.

Если, А > 1, то движение ротационное и х стремится либо к +а>, либо к -оо в зависимости от знака скорости.

Фазовый портрет 2я-периодичен по координате х. Рис. 16.

Вычислим наклон касательной к сепаратрисе, лежащей в верхней полуплоскости х > 0, при х -> л. Имеем.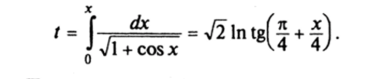

4. Рассмотрим задачу о движении гармонического осциллятора под действием периодической силы. Гармоническим осциллятором называется материальная точка, движущаяся под действием восстанавливающей силы, пропорциональной отклонению точки от некоторой фиксированной точки на прямой (например, начала координат), т. е. F = -сх. Если на точку массой т кроме восстанавливающей силы действует сила сопротивления — 2тех и периодическая сила тА cos со/, то уравнение ее движения примет вид.

Параметр е характеризует свойство вязкости внешней среды.

Рассмотрим различные ситуации.

• а) Свободные колебания гармонического осциллятора (е = А = 0). Общее решение уравнения (5.2) в этом случае имеет видх=/1_| cosv/ + ?Р А₂ sin W, v² = ст~‘ и описывает гармонические колебания на собственной частоте v. Произвольные постоянные А, А₂ определяются из начальных условий движения (х (0), х (0)). Полная энергия ½(тх² + cx²) = h сохраняется. Фазовые траектории С_А суть эллипсы, и движение по ним периодично с периодом 2nv^_1 (рис. 17, а).
• 0.5.3. Частота v называется собственной частотой колебаний гармонического осциллятора.
• б) Затухающие колебания гармонического осциллятора (А = 0). Если е положительно и v > е, то общее решение уравнения (5.2) в

этом случае имеет вид х = е^с'(Л, cosv. t + А₂ sin v.t), v. = Jv² — e² .

Рис. 17.

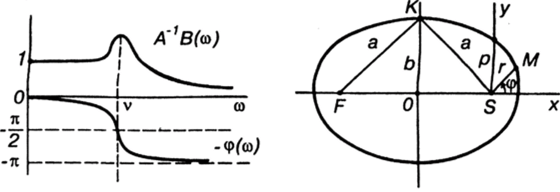
Рис. 18 Рис. 19.

Колебания затухают и x (t) стремится к нулю при t -* ю. Характер фазовой траектории представлен на рис. 17, б. Точка (0, 0) является положением равновесия, и все фазовые траектории стремятся к ней при I -> оо.

Если вязкость достаточно велика е > v, то движение теряет колебательный характер и x (t) монотонна, начиная с некоторого момента времени.

в) Если е * 0 и А * 0, то решение уравнения (5.2) складывается из общего решения однородного уравнения и его частного решения. Общее решение однородного уравнения при t -«оо затухает и при больших значениях времени не будет практически влиять на характер движения (см. п. б). Вынужденные колебания (частное решение), описываются соотношением

Колебания происходят на частоте вынуждающей силы и с амплитчпой R(ml и со спвигом (Ьаз mCmV гле.

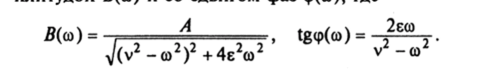
Зависимости амплитуды и фазы от частоты (амплитудно-фазовые характеристики) представлены на рис. 18.

Если частота вынуждающей силы ш совпадает с собственной частотой гармонического осциллятора v и сопротивление движению равно нулю (е = 0), то вынужденные колебания описываются уравнением.

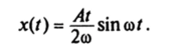
Амплитуда колебаний растет по линейному закону. Это явление называется резонансом.