Вероятностное пространство. 
Теория вероятностей и математическая статистика

В результате освоения материала данной главы студент должен: знать

• • теоретические основы понятия вероятности и вероятностного пространства;
• • классификацию вероятности — понятие классической, геометрической, условной вероятности;
• • теорему умножения вероятностей и ее следствия;
• • формулу полной вероятности и формулу Байеса (теорему гипотез); уметь
• • решать задачи на классическую, геометрическую, условную вероятности;
• • строить дерево вероятностей при решении задач на полную вероятность;
• • применять теорему гипотез; владеть
• • навыками решения вероятностных задач;
• • логикой рассуждений при нахождении апостериорной вероятности.

Понятие о вероятности и вероятностном пространстве

Теория вероятностей занимается изучением закономерностей, выраженных математически в числовом или формульном виде, которые возникают при совершении действий с заранее непредсказуемыми результатами. Каждое изучаемое нами действие назовем опытом, экспериментом или испытанием. Результат действия назовем элементарным исходом или элементарным событием и будем выражать его в числовом виде. Основное свойство исхода — его неделимость. Исход невозможно собрать из двух или нескольких действий.

В качестве примера рассмотрим действие: бросание кубика с изображенными на каждой грани цифрами от 1 до 6. Исходом каждого действия будет выявление цифры на верхней грани. Варианты с падением кубика на ребро или потерей кубика рассматривать не будем.

Все множество элементарных исходов назовем пространством элементарных исходов и обозначим буквой ?2. Сами элементарные исходы будем обозначать буквой со с индексом. Имеем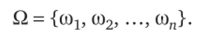

Определим понятие события как набора (множества) элементарных исходов. Например, выпадение четной цифры при бросании кубика — это событие. Оно реализуется при любом из элементарных исходов со₂, (0₄, со₆.

Набор элементарных исходов только в том случае имеет вероятностный признак, если:

• 1) обеспечены одинаковые условия проведения каждого опыта;
• 2) возможна многократная повторяемость опыта.

Все пространство элементарных исходов (элементарных событий), т. е. набор всех возможных исходов, представляет собой событие, которое произойдет всегда. Это достоверное событие (что-нибудь да выпадет). А вот цифру 7, например, сколько бы мы ни бросали кубик, мы не увидим. Это невозможное элементарное событие.

Элементарное событие назовем случайным, если оно может произойти в результате опыта, а может и не реализоваться. Два элементарных события назовем несовместными или непересекающимися, если они не могут произойти одновременно. Теперь можно уточнить понятие теории вероятностей.

Теория вероятностей — это наука о закономерностях массовых случайных событий, реализуемых в одинаковых, могущих повторяться неограниченное число раз условиях. Математические законы теории вероятностей не являются абстракциями, лишенными физического содержания. Они представляют собой математическое выражение реальных закономерностей, существующих в массовых случайных явлениях природы и общества.

Перейдем от понятия пространства элементарных исходов к понятию вероятностного пространства, представляющего собой среду, в которой:

• 1) существует пространство элементарных событий, имеющих вероятностный признак;
• 2) любое множество (событие) данного пространства должно быть наблюдаемым и измеримым;
• 3) каждому такому событию поставлено в соответствие некоторое число для сравнения событий по возможности их реализации.

Совокупность событий представляет собой некоторый класс подмножеств А, удовлетворяющий определенным условиям:

• 1) если подмножество, А принадлежит Д, то дополнение А также принадлежит Д (верна операция дополнения);
• 2) если подмножества А_г, А₂, …, А_п, … принадлежат Д, то и их счетное объединение А_г и А₂ и … и А_п и … принадлежит Д (верна операция объединения).

Из теории множеств известно, что операции над подмножествами могут быть получены с помощью двух операций дополнения и объединения. Поэтому можно сказать, что совокупность подмножеств, удовлетворяющих классу Д, замкнута относительно счетного числа операций. Говоря другими словами, совершая математические действия над зо подмножествами, принадлежащими Д и описывающими события, мы не получим результат, выходящий за рамки такой совокупности подмножеств, которой событие не соответствует.

Таким образом, под событием понимается не любое подмножество пространства, а только подмножество из выделенного класса А. Проблема замкнутости относительно счетного числа операций отпадает, если пространство элементарных исходов Q конечно или счетно (каждому исходу можно поставить определенное число из натурального ряда).

Как пример существования неизмеримых множеств рассмотрим элементарные исходы, являющиеся результатом бросания точки на отрезок [0; 1]. Мы производим измерение местоположения точки, которое естественно описываем рациональным числом. Множество рациональных точек, как известно, складывается из счетного числа точек. Оно является событием и также описывается рациональным числом. Но множество иррациональных точек есть дополнение к множеству рациональных точек, образуя вместе множество действительных чисел на отрезке. Значит, и множество иррациональных точек есть событие. Но, как указывают авторы учебника [3], «вряд ли естественно с физической точки зрения считать наблюдаемыми (и, следовательно, физически различимыми) событиями факты принадлежности точки к множеству рациональных и к множеству иррациональных чисел». В связи с этим не все множество чисел на отрезке [0; 1] является для нас наблюдаемым и измеримым.

Построим класс подмножеств Д, т. е. зададим совокупность этих чисел, поставленных в соответствие каждому событию вероятностного пространства. Тем самым введем понятие вероятности или вероятностной меры как числовой характеристики степени возможности появления какого-либо определенного события.

Пусть каждому событию, А поставлено в соответствие некоторое число Р (А), удовлетворяющее следующим аксиомам:

• 1) Р (А) > 0 (аксиома неотрицательности);
• 2) P (Q) = 1 (аксиома нормированное™);
• 3) Р (А_г +А₂ + … +А_п + …) = Р (А_:) + Р (А₂) + ••• + Р (Д,) + ••• для любых А, — п А; = 0, i Ф j (аксиома сложения несовместных событий).

Это число Р (А) называется вероятностью события А.

Рассмотрим свойства вероятности.

• 1. Вероятность есть теоретическая характеристика, вычисляемая по условиям схемы эксперимента, она не может быть получена экспериментально.
• 2. Вероятность дополнительного события равна

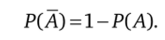
? Из равенства Q = А + А следует P (Q) = Р (А) + Р (А), или 1 = Р (А) + Р (А), откуда Р (А) = 1 — Р (А). ?

• 3. Вероятность невозможного события равна нулю: Р (0) = 0.
• ?Равенство следует из аксиомы сложения Л = А + 0.^
• 4. Вероятность заключена между нулем и единицей: 0 < Р (А) < 1.
• ?Поскольку ?2 = А + ?2 А, то1= Р (А) + Р (?2 А). Значит, 0 < Р (?2

А) = 1 — Р (А) по аксиоме неотрицательности. Тогда 0 < Р (А) < 1. ?

5. Вероятность сложения двух произвольных событий равна.

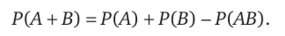
?Воспользуемся тем, что А + В= А + В АиВ = ВА + ВА. Из обоих равенств следует.

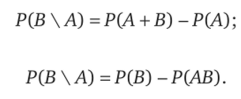
Вычтем из первого равенства второе, получим.

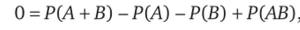
откуда и следует свойство 5.^.

Для трех произвольных событий справедливо равенство.

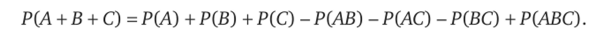
Для несовместимых событий, А и В их пересечение есть невозможное событие: АВ -0. Мы возвращаемся к аксиоме сложения несовместных событий:

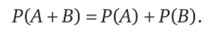
Таким образом, мы ввели понятие вероятностного пространства, обозначаемого обычно как {?2, А, Р}, где символы ?2, А и Р указывают на то, что мы имеем дело с пространством элементарных исходов, что, совершая операции с исходами, мы не выйдем за пределы измеримых подмножеств этого пространства (класс подмножеств А), что каждому исходу или событию соответствует некоторая вероятность его реализации Р. В дальнейшем изложении мы не будем ссылаться на измеримость множеств, считая их таковыми по умолчанию. Рассмотрение указанных вопросов выходит за рамки данной книги.

Пример 2.1. Рассмотрим эксперимент с бросанием симметричной монеты.

Естественным будет взять два события: выпадение «герба» (г) и выпадение.

«решки» (р), т. е. ?2 = {г; р}. Тогда класс подмножеств Д = {г, р, (г, р), 0}. Вероятности можно посчитать следующим образом:

Таким образом определена тройка {?2, Д, Р} — вероятностное пространство, в рамках которого можно рассматривать различные задачи.

Понимая, что ценность теоретических построений определяется их практической применимостью, привяжем понятие вероятности к практике, поставив в соответствие каждой возможности реализации события, А полученное экспериментальным путем некоторое число Р"(А).