Операции со случайными величинами

В результате освоения материала данной главы студент должен: знать

• • теорему о функции случайной величины;
• • основные правила арифметических операций со случайными величинами; уметь
• • совершать арифметические операции со случайными величинами из разных распределений;

владеть

• навыками совершения операций со случайными величинами.

Функции от случайных величин

В этой главе мы познакомимся с изменениями законов распределения, вызванными преобразованиями случайных величин. Пусть случайная величина Е, представленная значениями х_ь х₂, …, х_п, подвергается воздействию, преобразуясь в соответствии с правилом (р в случайную величину Г| (/Л — Ф (c)), значения которой оказываются равными соответственно у_ь у₂, …, у_п• Известен закон распределения величины Е,. Какой закон распределения будет иметь случайная величина Г|?

Дискретный тип распределения. Случайная величина с дискретна и имеет закон распределения, представленный в таблице.

Каждое значение х_; случайной величины Е, преобразуется в значение у, случайной величины ц в соответствии с правилом у/ = ср (х,-), имея ту же вероятность р,. Составим таблицу для значений случайной величины Г| и соответствующим ей вероятностям, упорядочив значения Г| по возрастанию и сложив вероятности одинаковых значений ц, если они возникнут. В результате получим закон распределения случайной величины тр

Пример 8.1. Случайная величина ?, имеет распределение, представленное в таблице. Найти закон распределения случайной величины г) =.

Решение. Составив таблицу соответствия значений г| их вероятностям (левая таблица) преобразуем ее в ряд распределения (правая таблица).

Закон распределения случайной величины ц, являющейся функцией двух или нескольких независимых случайных величин, строится аналогично. Рассмотрим дискретные случайные величины и ?₂, имеющие законы распределения, представленные в таблицах.

Пусть случайные величины ц, ^ и ?,₂ связаны функциональной зависимостью Г| = ф (^_1; ?₂). Для построения закона распределения Г) необходимо рассмотреть все возможные пары значений ^ и ^₂ и вычислить все возможные соответствующие им значения тр Привлечение каждой пары значений и ?₂ возможно с вероятностью, соответствующей произведению вероятностей отдельных значений. Например, вычисленному значению у₂₃ функции ф от значений аргументов ^ =х₁₂ и ^2=*23> т. е. У2з⁼⁽р (^12>^х2з1 соответствует вероятность P23=Pl2‘P23- Составляется таблица всех возможных значений г| и соответствующих этим значениям вероятностей:

Для преобразования полученной таблицы в закон распределения следует расположить значения ц в порядке возрастания, сложив вероятности при одинаковых значениях ц.

Пример 8.2. Случайные величины ?_а и ?₂ имеют распределения, представленные в таблицах. Найти закон распределения случайной величины Г) = 2?_х + 3^₂.

Решение. Все возможные значения Г) найдены и упорядочены по возрастанию:

Соответствующие им вероятности вычислены во второй строке таблицы, тем самым давая возможность представить закон распределения Г).

Непрерывный тип распределения. В непрерывном случае нахождение закона распределения сводится к вычислению плотности распределения вероятностей. Надо иметь в виду также, что важную роль играет монотонность функции преобразования одной случайной величину в другую Г) = cp (?,).

Теорема 8.1. Пусть для случайной величины 2, закон распределения вероятности задан плотностью р?(х). Случайная величина г) связана с ?, строго монотонной функциональной зависимостью г| = ф (?). Тогда закон распределения случайной величины г) имеет плотность распределения р_п(у) = р_?(х> х'_у [ гдех = ф-¹(у).

?Рассмотрим вначале случай монотонно возрастающей функции.

Функция распределения Рг|(у) может быть получена преобразованием функции распределения F^(x) случайной величины.

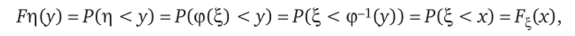
где х = ср^_1(у).

Плотность распределения случайной величины ц получается дифференцированием ее функции распределения:

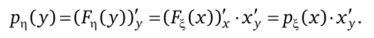
В случае монотонно убывающей функции появляется знак «минус»: 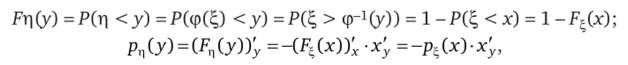где х^ < 0.

Объединяя формулы для возрастающей и убывающей функции т|=ф (?,), получим р_п (у) = р₄ (х> | х^, |, где х = ф-¹ (у). ?

Таким образом, зная одну из четырех функций F^(x), F^Cy), р^(х), р^Су) и строго монотонную функциональную связь между случайными величинами r| = (р (c)> можно вычислить остальные три функции. Представим результаты в виде схемы на рис. 8.1.

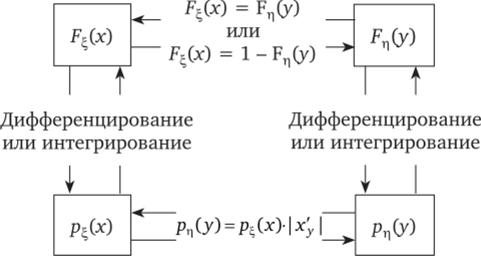
Рис. 8.1. Схема вычисления трех функций по заданной четвертой из набора R (x), F_M(y), р"(х), р_м(у), если 4 =.

Пример 8.3. Случайная величина равномерно распределена на отрезке [-1; 1]. Найти плотность распределения случайной величины г| = -1п (с, + 2).

Решение. Плотность равномерно распределенной случайной величины Е, равна.

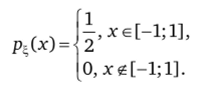
Функция у = -In (а^- + 2) является монотонно убывающей и дифференцируемой. Обратная функция х = е~У — 2 имеет производную х'_у = -е~У.

Скорректируем пределы интегрирования: если е [-1; 1], то ц е [-1пЗ; 0]. Плотность случайной величины ц будет иметь вид.

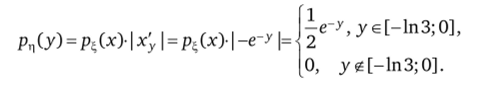
Замечание 8.1. Если функция ц = ф© немонотонна, закон распределения удается найти, разделив область значений на число промежутков, на каждом из которых функция обладает монотонной зависимостью. Тогда плотность распределения случайной величины ц будет иметь вид.

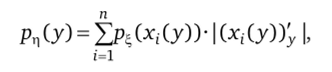
где п — число промежутков.

Замечание 8.2. Обычно математическое ожидание случайной величины Г) = ф (4) разыскивают через плотность р-,(х) случайной величины.

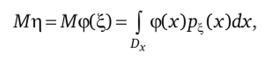
хотя, казалось бы, под знаком интеграла должна стоять плотность распределения случайной величины г|, т. е. должна быть использована формула Мр = j yp_n(y)dy, где D_x и D_y — области определения случайных.

°у

величин 4 и Г|.

Доказанная теорема дает ответ на этот вопрос. Пусть для случайной величины 4 закон распределения вероятности задан плотностью р=(х). Случайная величина р связана с 4 строго монотонной, например возрастающей, функциональной зависимостью р = ф©. Тогда