Законы отражения и преломления с точки зрения электромагнитной теории

Электромагнитная теория света получила признание, так как она легко объясняла практически все известные к моменту ее создания свойства света и оптические явления.

Рассмотрим отражение и преломление света с позиций электромагнитной теории (рис. 2.6). Пусть на границу раздела двух прозрачных сред, лежащую в плоскости XOY, падает под углом (-ij) плоская монохроматическая волна. Используя формулу Эйлера e^ia =cosa + i sina, уравнение падающей волны запишем в экспоненциальном виде:

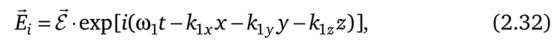
где ? — амплитуда колебаний электрического поля в падающей волне; k_lx, k_ly, k_lz — компоненты волнового вектора кг.

Для любого волнового вектора к справедливы следующие соотношения:

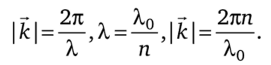
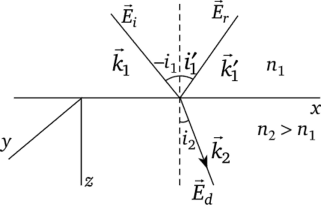
Рис. 2.6.

Для упрощения задачи можно положить, что колебания электрического поля Ё происходят в направлении оси у. Тогда вследствие поперечности электромагнитной волны проекция волнового вектора к_1у = 0.

В результате взаимодействия электромагнитной волны с границей раздела возникнут отраженная Ё_г и преломленная Ё_с1 волны:

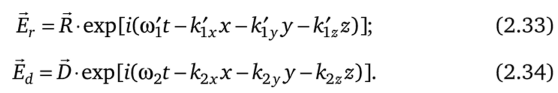
Так как свет имеет электромагнитную природу, его отражение и преломление должны подчиняться граничным условиям, справедливым для электрических и магнитных полей: сумма тангенциальных составляющих (обозначенных индексом т) векторов напряженностей Ё и Я на границе раздела в первой среде равна сумме тангельциальных составляющих векторов напряженностей? и Я на границе раздела во второй среде (верхним штрихом обозначены параметры отраженной волны):

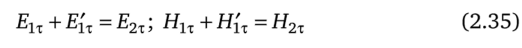
или (при z = 0).

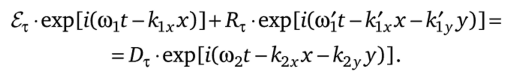
Эти граничные условия должны выполняться в любой момент времени и в любой точке на границе раздела двух сред, что возможно, если;

• 1) coj = со^ = со₂ — частота колебаний при преломлении и отражении не изменяется;
• 2) к_1у = к[_у = к_2у = 0 — падающий, отраженный и преломленный лучи лежат в одной плоскости с нормалью, восстановленной из точки падения;
• 3) к_1х =к{_х =к_2х. Из равенства к_1х = к{_х получаем закон отражения:
• 2к

к_г • sin (-i₁) = к{ • sin i{ или, так как к_г = к{ =—тг_ь sin (-i₁) = sin i{, -ц = i{.

Х₀

Закон преломления следует из равенства к_1х = к^:

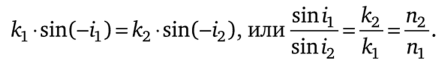
Далее рассмотрим переход световой волны из более плотной среды в менее плотную среду (п₂ < иД и связанное с таким переходом явление полного внутреннего отражения (ПВО). Будем, как и выше, считать, что волновой вектор лежит в плоскости XOZ (k_y = 0), E₂=D- exp[i (cot — к_2хх — k_2zz)]. _.

При п₂ < п_х проекция волнового вектора k_2z = у]к₂ ~Щ.х ^может оказаться либо вещественной, либо мнимой. В последнем случае это соответствует образованию во второй среде затухающей волны. Если к₂ > >к_1х(к_1х = к_2х), то k_2z> 0 — возникает незатухающая преломленная волна (в обоих случаях речь идет о прозрачной среде).

Если к₂ < к_1х, т. е., когда sin (-i₁)> —= —,.

К Щ

перед корнем физический смысл имеет только знак «-», так как в противном случае амплитуда преломленной волны по мере проникновения во вторую среду будет возрастать.

Представим k_2z в виде k_2z = —-, где.

h

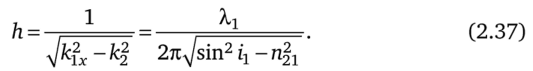
Тогда уравнение преломленной волны для рассматриваемого случая можно переписать в виде.

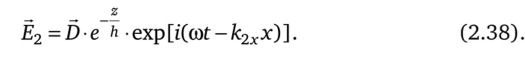
Z.

Выражение D? е h представляет амплитуду неоднородной волны, практически полностью затухающей на глубине z = h~₁; exp [i (cot -к_2хх)] — фазовый множитель, зависит только от координаты х, что означает распространение неоднородной волны (фазы) вдоль границы раздела сред со скоростью с/п₂- sin i₂.

Затухание волны не связано с поглощением, волна как бы в одном месте входит во вторую среду, далее распространяется вдоль границы и опять выходит в первую среду, но уже в другом месте, захватывая во второй среде область вблизи границы толщиной h ~ X.

Прямым доказательством справедливости данного механизма ПВО служит явление нарушенного полного внутреннего отражения (НПВО): если зазор между двумя однородными средами оказывается меньше глубины проникновения h неоднородной волны, то волна не испытывает отражения от зазора и полное внутреннее отражение нарушается.