Отношение порядка на множестве

Структура порядка может быть задана как на всем множестве М, так и на некотором его собственном подмножестве А, а М .

Определение 3.12. Рефлексивное антисимметричное и транзитивное отношение р с Л/ х Л/ называется отношением нестрогого порядка на (во) множестве М, а транзитивное асимметричное отношение (р на множестве М назовем отношением порядка на М, если при этом отношение ф линейно на М, т. е. определено для всех пар (а, Ь) из М х М, а ^ Ь, то отношение ф называется линейным порядком на множестве М. В противном случае множество М называется частично упорядоченным.

Примером частичного нестрогого порядка является отношение с включения (теоретико-множественного) на множестве Р (М) всех подмножеств множества М или на всем множестве U рассматриваемых нами множеств.

Пример 3.6. На рис. 3.9 построен граф отношения порядка по включению с на множестве Р (м) для М = {а, Ь, с).

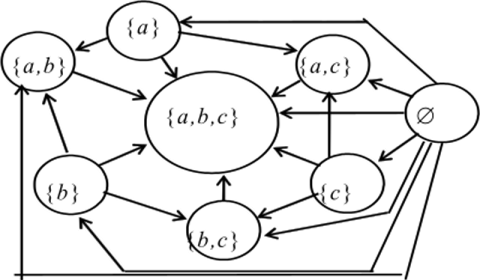
Рис. 3.9.

Пусть на М введена структура линейного порядка р так, что для каждого двухэлементного подмножества {а, b} будет либо (а, Ь) € р, либо (6, а) е р. Мы будем писать а ^Р<�Ь вместо (а, Ь) € р или еще короче так: а<�Ь, если речь идет об одном порядке, и будем говорить, что а меньше b или b больше а, или а предшествует /?, или b следует за а относительно порядка р. Каждая пара (а, Ь), где а < b, определяет в М подмножество 0(а, Ь) таких х, что а < х и х < b. Множество 0(а, Ь) назовем (а,^{-окрестностью} каждой его точки х или (<а, /^-интервалом. Для множества Л=[я,/?]= {a, b}(jO (a, b) элементы а и b назовем крайними (а — наименьшим, b — наибольшим в А) и будем писать я=inf А, /? = sup^.

Множество М называется вполне упорядоченным, если каждое его непустое подмножество имеет наименьший элемент.

Подмножество D с: М назовем дискретным, если для каждого элемента d из Z), кроме крайних в D, найдется пара (a, b) е М х М такая, что 0(а, b) = {d}.

Определение 3.13. Линейно упорядоченное множество F назовем конечным, если оно или пусто, или одноэлементно, или каждое его подмножество, кроме пустого и одноэлементных, имеет два крайних элемента: наименьший и наибольший. Линейно упорядоченное множество In назовем бесконечным, если хотя бы одно его подмножество имеет менее двух крайних элементов.

Пример 3.7. Для всякого действительного числа а конечным является множество F={jc: |лг| < а, х е Z} и бесконечным будет множество.

In={x :х>а, х е Z}.

Упражнение 3.6. Доказать бесконечность множества.

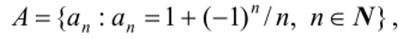
если порядок в А есть естественный порядок из R (о множестве N см. в п. 3.6).

Теорема о бесконечности. У каждого бесконечного множества In множества как конечных подмножеств, так и подмножеств бесконечных бесконечны.

Теорема о конечности. Множество конечных подмножеств конечного множества F конечно.

Доказательства этих двух теорем Читатель легко может получить из Определения 3.13.

Определение 3.14. Линейно упорядоченное множество В называется всюду плотным, если для каждого его подмножества {а, Ь}, а<�Ь,.

найдется такой элемент сеВ, что, а <�с<�Ь.

Например, множество рациональных чисел Q всюду плотно по отношению естественного порядка в Q из R.

Утверждение 3.4. Множество М, бесконечное относительно линейного порядка р на М, будет бесконечным и относительно любого иного линейного порядка на М.

Это утверждение, которое мы оставляем без доказательства, говорит об инвариантности понятия бесконечности множества относительно замены порядка на этом множестве, и следовательно, о возможности определения бесконечности множества без привлечения понятия порядка. Это было сделано в конце XIX века Рихардом Дедекиндом (1.10.1831— 12.02.1916) [15, с. 265]. Корректность такого определения ставится под сомнение результатами автора книги (п.п. 3.7.7 и 6.2).

С другой стороны, для всюду плотного, относительно порядка р, множества М можно указать некоторый порядок ф, относительно которого множество М будет иметь дискретную структуру. Обо всем этом немного подробнее мы скажем в дополнительном п. 3.7.