Конструкция и геометрия гребного винта

Наибольшее распространение на кораблях и судах всех типов получил гребной винт, поэтому в дальнейшем только его и будем рассматривать.

Винт состоит из ступицы и лопастей, являющихся его рабочими элементами. За счет разницы давлений на засасывающей, обращенной в сторону движения, и нагнетающей, воспринимающей реакцию отброшенных масс воды, поверхностях лопастей создается упор гребного винта.

Лопасть — крылообразное тело, создаваемое двумя винтовыми поверхностями, линия пересечения которых называется контуром.

Как и у крыла, у лопасти различают две кромки — входящую, направленную навстречу потоку, и выходящую — противоположную первой. Граница между ними — край лопасти — самая удаленная от оси точка гребного винта. Участок, примыкающий к ступице, называется корнем лопасти.

Кратко остановимся на винтовых поверхностях, от которых самый распространенный движитель — гребной винт — получил свое название.

Заставим отрезок АВ двигаться таким образом, чтобы один его конец — точка А — скользил по оси цилиндра, а другой — точка В — по его поверхности, одновременно вращаясь вокруг оси. Образованная таким образом поверхность носит название винтовой (рис. 4.9). Если скорости, поступательная и окружная, будут при этом постоянными, то образуется правильная винтовая поверхность. Точка В на боковой поверхности цилиндра опишет винтовую линию, шагом которой называется расстояние Р, проходимое этой точкой в осевом направлении за один оборот.

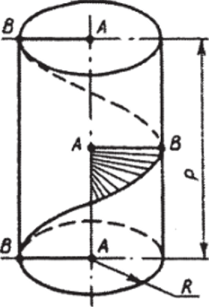
Рис. 4.9. Образование винтовой поверхности.

Рассекая винтовую поверхность соосными цилиндрами, на каждом из них получим винтовую линию — след движения соответствующей точки отрезка АВ. Следовательно, винтовую поверхность можно определить как совокупность бесконечного множества винтовых линий, описанных точками отрезка АВ. Сам этот отрезок называется образующей винтовой поверхности. Он в общем случае может быть наклонен к оси цилиндра, иметь криволинейную форму.

Разворачивая боковую поверхность цилиндра на плоскость, получим прямоугольник, в котором винтовая линия является диагональю. Нижняя половина этого прямоугольника называется шаговым треугольником: его катеты равны длине окружности и шагу винтовой линии. Если гипотенуза такого треугольника прямолинейная (рис. 4.10, а), то винтовая линия называется винтовой линией.

^ (Р

постоянного шага, при этом шаговый угол.

KU ^

Криволинейная гипотенуза — признак винтовой линии переменного шага <�р = /(у), где у — угол поворота образующей относительно оси цилиндра.

Правильная винтовая поверхность на всех радиусах в сечении имеет винтовые линии постоянного шага. Кроме того, соблюдается и условие Р = const. Если же поверхность образована винтовыми линиями постоянного шага, но Р =* /(г), то это винтовая поверхность радиально-переменного шага. Различают еще винтовую поверхность аксиально-переменного шага — шаговые треугольники имеют криволинейные гипотенузы (ф — const), но один и тот же средний шаг Р = const. Если ф * const и Р * /(г), то такая поверх;

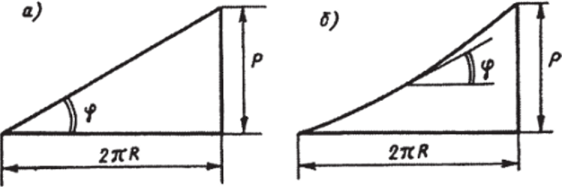
Рис. 4.10. Шаговый треугольник: а — винтовая линия постоянного шага; б — винтовая линия переменного шага ность называется винтовой поверхностью аксиально-радиальнонеременного шага.

Лопасти гребных винтов образуются винтовыми поверхностями всех перечисленных типов. Так, если нагнетающая поверхность лопасти может быть правильной, то засасывающая всегда имеет в сечении винтовую линию переменного шага.

Рассекая лопасть гребного винта соосным с ним цилиндром и разворачивая его на плоскость, получаем профиль сечения лопасти, шаг и шаговый угол на данном радиусе (рис. 4.11).

Винтовая поверхность без искажений не разворачивается на плоскость. Наиболее точное представление о форме и площади лопасти дает так называемый спрямленный контур, построение которого осуществляется известными методами графики.

Основные геометрические характеристики гребного винта — число лопастей, диаметр, шаг, диаметр ступицы, форма профиля лопасти, площадь ее спрямленной поверхности. Современные гребные винты имеют диаметр до D = 12 м, масса такого движителя может достигать 150 т. Число лопастей винтов изменяется в пределах Z_p — 2-^8.

Наряду с диаметром гребной винт характеризуют его безразмерные геометрические характеристики. К ним относят:

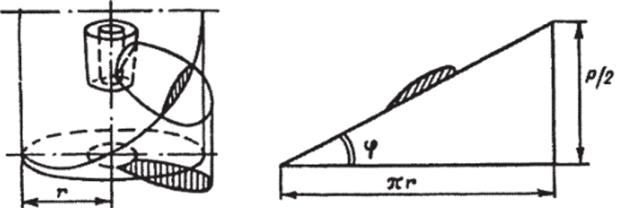
Рис. 4.11. Сечение лопасти гребного винта соосным цилиндром.

• — дисковое отношение Л_Е/Л₀, где А_Е — площадь спрямленной поверхности всех лопастей; А₀— площадь диска (гидравлического сечения) гребного винта; А_Е/А₀ = 0,2+1,3 (большие значения относятся к винтам быстроходных судов);
• — шаговое отношение P/D, где Р — шаг; D — диаметр винта, P/D — 0, б-ь2,0 (большие значения — винты быстроходных судов);
• — относительный диаметр ступицы d" -d_xx/D = 0,16−5-0,35 (большие значения характерны для ВРШ и винтов со съемными лопастями).

Если относительно наблюдателя, смотрящего в корму удаляющегося судна, гребной винт вращается по часовой стрелке, то его называют винтом правого вращения, в противном случае — винтом левого вращения.