Рисковая премия. 
Страхование

Премия, которая рассчитывается на основе принципа эквивалентности и обеспечивает его соблюдение, называется " рисковая премия" . Она соответствует стоимости того отдельного риска, который страховщик принимает на себя по договору страхования.

Для вывода формул расчета рисковой премии на основе принципа эквивалентности вначале производится оценка ожидаемой стоимости обязательств сторон. Приравнивая их, получают уравнение, где величина премии в обязательствах страхователя является неизвестным. В результате его решения в общем виде получают необходимые расчетные зависимости. Проиллюстрируем это на небольшом примере.

Пример. Эквивалентная стоимость риска

В предыдущем примере риск автовладельца до его участия в страховом фонде состоял в следующем: с определенной вероятностью q он мог потерять автомобиль стоимостью s; а с вероятностью (1 — q) он ничего не терял, т. е. его убытки были равны 0.

Этот риск автовладелец передал страховому фонду. Ожидаемая стоимость такого риска по определению математического ожидания равна сумме произведений возможных значений случайной величины на вероятность их наступления, т. е.

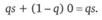
За передачу риска владелец автомобиля уплатил в страховой фонд определенную сумму (страховую премию) П. Эта премия подлежала уплате безусловно при вступлении в фонд, поэтому расходы автовладельца в любом случае составляли П. Произошел обмен случайного риска наступления катастрофического убытка (хищения автомобиля) на фиксированный (неслучайный) убыток, равный страховой премии.

Данный обмен должен строиться на эквивалентной основе. Принцип эквивалентности, лежащий в основе передачи риска в страховании, подразумевает равенство ожидаемых стоимостей обязательств сторон. Это означает, что ожидаемая стоимость премий по договору должна быть равна ожидаемой стоимости выплат. В нашем случае премия уплачивается безусловно, ее ожидаемая стоимость равна фактической, поэтому можно записать.

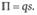
Если подставить численные значения из предыдущего примера, то получаем уже знакомый результат:

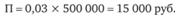
Рассчитанная таким образом величина премии является справедливой платой за страхование, эквивалентной тому риску, который передает данный участник в страховой фонд.

В рассмотренном примере срок страхования составлял всего один год, и принцип эквивалентности применялся в упрощенной формулировке, не учитывавшей изменение стоимости денег во времени и дополнительный доход от инвестирования. Кроме того, страховая премия в обязательном порядке полностью уплачивалась в момент начала страхования. Поэтому ее ожидаемая стоимость совпадала с фактической. В результате рисковая премия оказалась равной ожидаемой стоимости выплат по договору:

Подобная ситуация характерна для большинства видов имущественного и личного страхования, кроме страхования жизни.

Рисковая надбавка

Если каждая рисковая премия эквивалентна ожидаемому убытку по договору, то их сумма будет равна ожидаемой совокупной величине выплат по всему портфелю. То есть чистые справедливые премии являются достаточными, если фактическая сумма выплат не превысит ожидаемую. Но на практике могут иметь место отклонения от ожидаемых значений как в меньшую, так и в большую сторону. Подобные колебания являются следствием действия особых рисков, которые возникают в результате объединения договоров в один портфель.

Прежде всего, для любого страхового портфеля всегда существует риск случайности. Даже если известны объективно существующие теоретические вероятности наступления страховых случаев и распределение выплат, предсказать конкретные значения, которые примут случайные величины, невозможно (поэтому они и называются случайными). Даже для огромных совокупностей закон больших чисел не гарантирует равенства фактических средних величин ожидаемым. Он лишь позволяет оценить интервал, в который с заданной вероятностью попадет это значение. Ширина такого интервала зависит от количества рисков в портфеле. Чем их больше, тем менее вероятны большие отклонения от ожидаемых значений. Но такая вероятность, пусть и очень малая, всегда существует.

При расчете рисковых премий ориентируются на ожидаемые значения. Но никто не знает истинных (теоретических) ожидаемых значений количества страховых случаев и убытков ни для отдельного договора, ни для портфеля в целом. На практике их приходится оценивать на основе имеющейся статистики. Получаемые оценки всегда в той или иной мере отличаются от истинного значения. Это привносит в деятельность страховой компании дополнительную неопределенность, которую называют риском оценки.

Статистические данные, на основе которых оцениваются случайные величины, собраны в прошлых периодах. Однако в будущем уровень «опасности» может измениться. Это относится ко всем областям человеческой жизни. Климатические изменения влияют на вероятность природных катастроф. Благодаря научному прогрессу появляются новые виды техники, свойства которых еще плохо изучены. Развитие медицины снижает риск смертности и увеличивает продолжительность жизни. Поэтому тарифы, рассчитанные методически верно по абсолютно надежным оценкам, могут оказаться недостаточными. Требуется прогнозирование изменения уровня «опасностей» во времени. В результате возникает так называемый риск прогноза.

Все три составляющие неопределенности, присущие страхованию, объединяются общим понятием «технический страховой риск». Из-за его наличия в деятельности каждого страховщика всегда есть вероятность неблагоприятного отклонения фактической суммы убытков по портфелю от ее ожидаемой величины. Для компенсации возможных отклонений страховая компания может использовать собственные или заемные средства либо заранее сформированные специальные резервы. Одним из основных источников средств покрытия данного риска является рисковая (или гарантийная) надбавка.

Для случайной величины вероятность принять значение больше или меньше математического ожидания равны 50%. Поэтому рисковая премия, которая ориентируется на ожидаемые значения, будет достаточна лишь в половине случаев. Дополнение ее рисковой надбавкой увеличивает вероятность безубыточной работы компании до некоторого заданного страховщиком уровня, который называется «гарантия безопасности» .

Ее практическая величина находится в пределах от 95 до 99,99%, но никогда не может достичь 100%. Это можно объяснить следующим образом. Если страховщик хочет абсолютно достоверно обеспечить превышение премий над выплатами, он должен сформировать страховой фонд в размере совокупной страховой суммы. В этом случае премия по каждому договору будет равна страховой сумме. Разумеется, такие условия являются неприемлемыми для страхователей. Поэтому компании вынуждены принимать гарантию безопасности меньше 100%, хотя и достаточно близкую к ней. Таким образом, даже введение в премию рисковой надбавки может гарантировать безубыточность работы только с некоторой, пусть и очень большой, вероятностью.

Пример. Рисковая надбавка

В предыдущих примерах мы рассматривали портфель по страхованию автомобилей на случай хищения, подчиняющийся действию закона больших чисел. Для оценки каждого отдельного риска используются ожидаемые значения убытков. Тем самым обеспечивается эквивалентность обязательств сторон. Но насколько можно быть уверенным, что данных премий хватит на все выплаты?

Портфель состоит из п = 1000 договоров. Размер убытка при страховом случае фиксирован и соответствует стоимости автомобиля s = 500 000 руб. Поэтому общая сумма выплат по портфелю определяется одной случайной величиной — количеством хищений. По каждому договору страховой случай может наступить с вероятностью q = 0,03. Если все договоры независимы, то число угонов в таком портфеле является дискретной случайной величиной, распределенной по биномиальному закону.

Рисковая премия по договору была определена в размере.

0,03×500 000 = 15 000 руб.

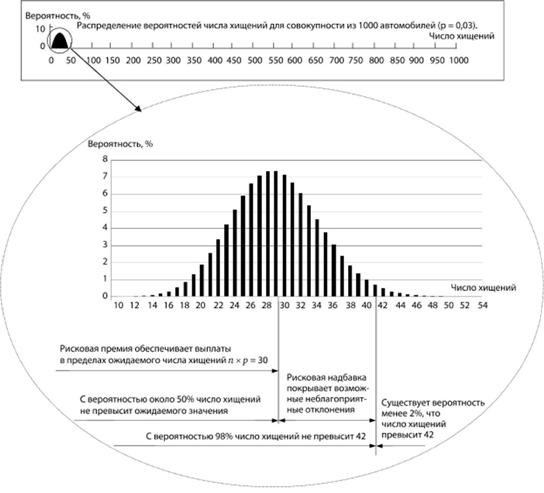
Рис. 5.1. Иллюстрация к расчету рисковой надбавки Их суммы хватит на выплаты, если число угонов не превысит ожидаемого значения, которое равно.

п x р = 1000×0,03 = 30.

Вероятность данного события (m = 30), определенная по биномиальному закону, равна 55%. В остальных 45% случаев число угонов окажется выше ожидаемого, и рисковых премий будет недостаточно. Разумеется, для практической работы такой уровень безопасности неприемлем. Требуется рисковая надбавка, которая обеспечит компенсацию возможных неблагоприятных отклонений фактических выплат от ожидаемых и тем самым повысит вероятность безубыточной работы до заданного уровня гарантии безопасности 98−99,99%.

Для рассматриваемого портфеля рисков количество угонов, которое с вероятностью 98% не будет превышено, составляет 42. При гарантии безопасности, равной 99,99%, это значение увеличивается до 52 (рис. 5.1)!

Если установлен уровень безопасности 98%, размер фонда должен быть достаточным для оплаты 42 угонов. Рисковые премии гарантируют выплату лишь по ожидаемым 30 страховым случаям. Рисковая надбавка должна дать возможность страховой компании, если потребуется, осуществить еще 12 выплат.

Сумма рисковой надбавки, приходящаяся на один договор, составит.

12×500 000 / 1000 = 6000 руб.

Тогда страховая премия, которая обеспечит вероятность неразорения 98%, должна быть равна.

15 000 + 6000 = 21 000 руб. вместо 15 000 руб. «чистой» премии.

По отношению к рисковой премии надбавка составляет.

6000 / 15 000 = 0,4 = 40%.

Это значительная величина. Если же страховщику удалось в одном портфеле объединить не 1000 рисков, а 5000, то при том же уровне безопасности 98% надбавка составит уже 2500 руб. на договор, т. е. всего около 17% от рисковой премии. Для портфеля из 10 000 договоров ее величина уменьшится до 12%.

Данный эффект проявляется в результате действия закона больших чисел. Чем больше множество случайных величин, тем менее вероятны отклонения средних значений от ожидаемых. Для страховой компании увеличение портфеля означает возможность сделать меньше надбавку к премии и тем самым снизить цену страхования. Это дает серьезное конкурентное преимущество крупным страховым компаниям.

Задача расчета рисковой надбавки достаточно сложна. Для ее решения необходимо, во-первых, определить требуемую общую сумму рисковых надбавок и, во-вторых, установить «справедливый» принцип деления этой общей суммы между всеми договорами.

В рассмотренном примере общая сумма рисковых надбавок определялась на основе предположения о биномиальном распределении совокупного убытка по портфелю. Затем она делилась поровну между всеми участниками, поскольку по условиям все застрахованные риски были одинаковы. На практике в портфеле объединяются разные по степени «опасности» договоры, и совокупный убыток может иметь более сложное распределение. Поэтому существуют различные подходы к делению надбавки: принцип математического ожидания (т.е. пропорционально рисковой премии), принцип среднеквадратического отклонения, принцип дисперсии и т. д. Возможны также их комбинации.

Величина рисковой надбавки зависит от заданного уровня гарантии безопасности и разброса совокупного убытка относительно ожидаемого значения. Последний, в свою очередь, определяется количеством договоров в портфеле и дисперсией (среднеквадратическим отклонением) рисков, составляющих данный портфель.