Другие вероятностные методы построения выборки

Наряду с описанными четырьмя основными методами построения выборки существуют и другие, разработанные специально для решения каких-либо специфических проблем (большинство из них представляют собой модификации основных методов). Рассмотрим лишь две из этих модификаций, имеющие определенное отношение к маркетинговым исследованиям: последовательное построение выборки (sequential sampling) и двойное или двустадийное построение выборки (double sampling, two-phase sampling).

При последовательном построении выборки ее размер заранее не определяется. Определяется лишь правило, на основании которого принимается решение о необходимом размере выборки. Данные собираются поэтапно. По окончании каждого этапа отбора данные анализируются и принимается решение о необходимости продолжения отбора.

Такой метод построения выборки удобен, например, когда возникает альтернатива. На каждой стадии респондентов спрашивают, какой из двух возможных товаров они бы предпочли. Когда их предпочтения становятся ясны с достаточно высокой степенью достоверности, процесс сбора новых данных прекращается.

При двойном (двустадийном) построении выборки на первой стадии строится большая по объему выборка и проводится краткий опрос. На основе этой информации строится небольшая выборка из элементов, охваченных первым опросом, и собирается дополнительная, углубленная информация.

Такой метод полезен, когда невозможно получить основу для построения требуемой выборки, но известно, что она составляет часть основы для более широкой выборки. Тогда на первой стадии выясняется, например, кто из респондентов пьет яблочный сок и в каком примерно объеме, а на второй стадии строится выборка, стратифицированная по объему потребления сока, и собирается информация, например, о тонкостях выбора. Если стратификация не проводится, стадии могут проводиться одновременно.

Сравнительные характеристики и краткая схема использования основных методов построения выборки

Завершая рассмотрение методов построения выборки, приведем результаты их краткого сопоставительного анализа (табл. 9.3).

Таблица 9.3. Сравнительные характеристики разных методов построения выборки

Простая случайная выборка (simple random sampling, или SRS).

• 1. Подбирается подходящая основа выборки.
• 2. Элементы нумеруются от 1 до N (размера выборки).
• 3. Генерируется на компьютере или находится в таблице n (размер выборки) различных случайных чисел в интервале от 1 до N.
• 4. В выборку включаются единицы отбора с соответствующими номерами.

Систематическая случайная выборка (systematic sampling).

• 1. Подбирается подходящая основа выборки.
• 2. Элементы нумеруются от 1 до N (размера выборки).
• 3. Определяется шаг выборки :
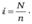• 4. Выбирается случайное число r на интервале от 1 до i.
• 5. В выборку включаются элементы с номерами r, r + i, r + 2i, r + 3i, …, (n — 1) i. Если это дроби, они округляются до ближайшего целого числа.

Метод стратификации (stratified sampling)

• 1. Подбирается подходящая основа выборки.
• 2. Подбирается одна или несколько переменных стратификации и выбирается число страт Н.
• 3. Исследуемая совокупность разделяется на Н страт так, что каждый элемент входит в одну и только одну страту в зависимости от значений параметров стратификации.
• 4. Элементы, входящие в каждую страту, нумеруются от 1 до Nh, где Nh — число элементов исследуемой совокупности в страте.
• 5. На основе пропорционального или непропорционального отбора определяется размер выборки, извлекаемой из каждой страты nh, где
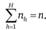
• 6. В каждой страте извлекается простая случайная выборка размером nh.

Метод кластеризации (cluster sampling)

Опишем процедуру двустадийного пропорционального отбора, так как чаще всего используется именно она.

• 1. Исследуемая совокупность разделяется на С кластеров, из которых с будут включены в выборку.
• 2. Элементы исследуемой совокупности нумеруются от 1 до N так, что сначала перенумеровываются элементы первого кластера, затем — второго и т. д.
• 3. Рассчитывается шаг отбора i, 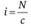. Если это дробь, она

округляется до ближайшего целого числа.

• 4. Как при построении систематической случайной выборки в интервале от 1 до г, выбирается случайное число r.
• 5. Выявляются элементы с номерами r, r + i, r + 2i, r + 3i,…, r + (с — 1) i. Если это дроби, они округляются до ближайшего целого числа.
• 6. Отбираются кластеры, содержащие выявленные элементы.
• 7. В каждом кластере путем простого или систематического отбора выбираются единицы отбора. Число единиц отбора из каждого кластера примерно одинаково и равно .
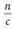• 8. Если число элементов в каком-либо кластере превышает шаг отбора, этот кластер будет отбираться вне зависимости от того, какое случайное число выпало на четвертом шаге алгоритма. Такой кластер включается в выборку и исключается из дальнейшего рассмотрения. Рассчитывается новый размер исследуемой совокупности N*, новое число кластеров, которые должны отбираться случайным образом с* (равное с — 1) и новый шаг отбора г*. Такая процедура повторяется до тех пор, пока число элементов во всех кластерах не станет меньше шага отбора. Если b кластеров отбираются с определенностью, то остальные с-b кластеров отбираются в соответствии с процедурой, описанной в пунктах 1−7. На одну единицу отбора, которая должна попасть в выборку, приходится в среднем 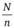единиц отбора в исследуемой совокупности. Поэтому из b кластеров, с определенностью представленных в выборке, отбирается число единиц отбора, определяемое по формуле

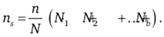(9.4).

Соответственно на кластеры, отбираемые случайным образом, приходятся остальные n* = n — ns единиц отбора.