Математическое программирование. 
Моделирование систем и процессов

Методы математического программирования позволяют вычислить точки минимума функционалов на множествах конечномерных пространств. Методы оптимизации предназначены для вычисления минимизирующих или максимизирующих элементов функционалов в соответствующих пространствах, определяющих оценки для выбора вариантов.

Классификация задач математического программирования

Существуют различные способы формулировки и формализованной записи задачи математического программирования. В этих постановках в той или иной форме отображаются целевая функция и ограничения.

В зависимости от вида целевой функции и ограничений сформировался ряд классов задач математического программирования (табл. 2.1).

Задачи перечисленных разделов обладают общим свойством: всякая точка локального минимума является оптимальной точкой. Несколько в стороне находятся так называемые многоэкстремальные задачи — задачи, для которых указанное свойство не выполняется.

Таблица 2.1. Классификация задач математического программирования

Способ нахождения экстремума определяется классом задачи. Но перед тем как получить математическую модель, нужно выполнить четыре следующих этапа моделирования.

• • Определение границ системы оптимизации. Отбрасываем те связи объекта оптимизации с внешним миром, которые не могут сильно повлиять на результат оптимизации, а точнее те, без которых решение упрощается.
• • Выбор управляемых переменных. «Замораживаем» значения некоторых переменных (неуправляемые переменные). Другие оставляем принимать любые значения из области допустимых решений (управляемые переменные).
• • Определение ограничений на управляемые переменные (равенства и (или) неравенства).
• • Выбор числового критерия оптимизации (например, показателя эффективности).

Создаем целевую функцию.

Виды методов математического программирования

Методы математического программирования можно разделить на несколько групп в зависимости от типа допустимых областей, методов формирования вычислительной схемы и других признаков.

По типу допустимых областей, в которых выполняется минимизация, можно выделить две группы методов:

— методы безусловной минимизации (максимизации) функционалов, когда допустимой областью изменения аргументов функционала является конечномерное пространство; к таким методам относятся методы наискорейшего спуска, методы Ньютона, методы сопряженных направлений (градиентов) и др.;

методы условной минимизации (максимизации), когда допустимым множеством является часть пространства. По типу вычислительных алгоритмов можно выделить:

• — методы последовательного уменьшения функционала;
• — методы, использующие необходимые условия оптимальности.

Методы безусловной минимизации

Для минимизации функционала без ограничений (во всем конечномерном пространстве): ф (.г), х е К" , т. е. когда ограничения отсутствуют, можно использовать два метода:

— метод последовательной (прямой) оптимизации, когда вычислительный алгоритм формирует минимизирующую последовательность на основе антиградиента функционала:

сходящуюся к минимизирующему элементу х';

— метод необходимых условий, когда минимизирующий элемент вычисляется на основе необходимых условий оптимума.

Если в методе последовательной минимизации непосредственно формируется минимизирующая последовательность, то метод необходимых условий формулирует условия, которым должен удовлетворять вектор х*. Очевидно, что для вычисления вектора х* из необходимых условий следует также построить последовательность хА+, = |{хА), х0 = х (|, сходящуюся к решению системы необходимых условий (2.3.2) из начальной точки х0 = х°. Таким образом, в двух случаях строятся минимизирующие последовательности.

Методы выпуклой условной минимизации

Общая постановка задач конечномерной оптимизации имеет следующий вид: вычислить векторы, доставляющие минимум выпуклых функционалов.

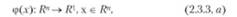
при ограничениях, задающих выпуклую допустимую область О изменения аргументов функционала:

где функционал (целевая функция или критерий) определяет цель и количественное выражение эффективности решения; х е Я"  — вектор переменных (управлений, решений и т. д.), такой, чтох = (.*" х{, х")Т;gi (х{), г = 1, тп — функции, задающие ограничения в виде допустимой выпуклой области конечномерного пространства.

Рассмотрим идеи методов, лежащие в основе решения общих задач математического программирования с ограничениями: вычислить минимум функционала <�р (х) при выполнении ограничений.

Для решения экстремальной задачи можно построить итерационные проекционные алгоритмы минимизации с восстановлением ограничений:

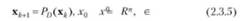
где Рв () — оператор проецирования антиградиента функционала [-Эф/Э.г] в точке хк на допустимое выпуклое множество.

Проектор вычисляет элемент Р0(х), удовлетворяющий условию:

причем оператор Р0(х) называется оператором проецирования (проектором) элемента х на выпуклое множество Д, а использованная норма — норма евклидова пространства.

Существуют алгоритмы минимизации с сохранением ограничений задачи:

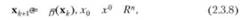
где оператор (2.3.8) задает алгоритм с проверкой условий оптимальности на основе теоремы Куна — Таккера.

Таким образом, для минимизации функционала формируется минимизирующая последовательность типа (2.3.8) с проверкой на каждой итерации выполнения необходимых условий. К таким процедурам относятся методы линейного, квадратичного программирования и другие методы.

Обсудим другую идею вычисления оптимальных решений. Сущность ее заключается в использовании проектирования на допустимые выпуклые множества точек, совпадающих с безусловным минимумом функционала. Необходимо учесть ограниченность данного метода, поскольку корректное решение имеет место для «функционалов равного роста» из точки безусловного минимума. Тогда для задачи: вычисли ь.

решение принимает вид.

где Рр (-) — проектор на выпуклое допустимое множество О, а х° е Я" — точка безусловного минимума функционала.