Выборочное наблюдение. 
Статистика

Цели и этапы выборочного наблюдения

Выборочное наблюдение в настоящее время находит достаточно широкое применение в обследованиях промышленных и сельскохозяйственных предприятий, бюджетов и занятости населения, изучении цен на потребительском рынке. Выборочный метод является важнейшим источником информации в контроле качества продукции, маркетинговых и социологических исследованиях.

Выборочным наблюдением называется такое несплошное обследование, при котором признаки регистрируются у отдельных единиц изучаемой статистической совокупности, отобранных с использованием специальных методов, а полученные в процессе обследования результаты с определенным уровнем вероятности распространяются на всю исходную совокупность.

Выборочное наблюдение нельзя отождествлять с несплошным обследованием вообще, так как оно является лишь одним из видов последнего, наиболее проработанным с методологической и организационной точек зрения.

Помимо выборочного наблюдения несплошное обследование может осуществляться путем монографического описания, методом основного массива или на основе различных видов анкетирования, когда отсутствуют какие-либо специальные методы отбора респондентов и процент заполненных и возвращенных анкет заранее не известен.

Преимущества выборочного наблюдения заключаются в существенной экономии различного вида ресурсов, а именно:

• а) финансовых средств, затрачиваемых на сбор и обработку данных, подготовку и оплату персонала;
• б) материально-технических ресурсов (канцелярские товары, оргтехника, расходные материалы, транспортное обслуживание и т. п.);
• в) трудовых ресурсов, привлекаемых к обследованию на всех его этапах;
• г) сокращении времени, затрачиваемого как на получение первичной информации, так и на ее последующую обработку вплоть до публикации итоговых материалов.

В то же время необходимо четко представлять, что выборочное наблюдение, как бы грамотно с методологической точки зрения оно не было организовано, всегда связано с определенными, пусть небольшими и измеряемыми ошибками. Поэтому когда вариация регистрируемых признаков очень сильная и процент отбора для получения выборочных значений с заданной точностью достигает 20—25%, следует правильно оцепить целесообразность несплошного обследования, сопоставив достаточно большие затраты всех ресурсов на такую объемную выборку и ожидаемые погрешности статистических характеристик. Вполне вероятно, что проведение сплошного обследования в подобных случаях будет более оправданным.

С другой стороны, при решении ряда задач выборочное наблюдение является единственно возможным способом получения необходимой информации. Так, контроль многих видов продукции связан с их порчей, потерей товарного вида, нарушением герметизации. Например, нельзя проверить каждую производимую предприятием электролампу на соблюдение требований по продолжительности горения. Невозможно проверить на соответствие стандартам каждый пакет с соком или молочной продукцией, так как это связано с вскрытием их упаковки. В подобных случаях контроль качества может осуществляться только с использованием выборочного метода.

Реализация выборочного метода базируется па понятиях генеральной и выборочной совокупностей.

Генеральной совокупностью называется вся исходная изучаемая статистическая совокупность, из которой на основе отбора единиц или групп единиц формируется совокупность выборочная. Поэтому генеральную совокупность также называют основой выборки.

Отбор единиц в выборочную совокупность может быть повторным или бесповторным.

При повторном отборе попавшая в выборку единица подвергается обследованию, т. е. регистрации значений ее признаков, возвращается в генеральную совокупность и наравне с другими единицами участвует в дальнейшей процедуре отбора. Таким образом, некоторые единицы могут попадать в выборку дважды, трижды или даже большее число раз. И при изучении выборочной совокупности они будут рассматриваться как отдельные независимые наблюдения.

Отметим, что число единиц генеральной совокупности, участвующих в отборе, при таком подходе остается постоянным. Поэтому вероятность попадания в выборку для всех единиц совокупности на протяжении всего процесса отбора также не меняется.

На практике методология повторного отбора обычно используется в тех случаях, когда объем генеральной совокупности не известен и теоретически возможно повторение единиц с уже встречавшимися значениями всех регистрируемых признаков.

Например, при проведении маркетинговых исследований нельзя сколько-нибудь точно оценить, какое число потребителей предпочитают стиральный порошок конкретной торговой марки, сколько покупателей предпочитают делать покупки именно в данном супермаркете и т. д. Поэтому возможно повторение совершенно идентичных единиц как по причине практически неограниченных объемов совокупности, так и вследствие возможной повторной регистрации. Предположим, при проведении обследования один и тот же покупатель может дважды прийти в магазин и дважды подвергнуться обследованию.

При выборочном контроле качества продукции объем генеральной совокупности также часто не определен, так как процесс производства может осуществляться постоянно, каждый день дополняя генеральную совокупность новыми единицами — изделиями. Поэтому в выборочную совокупность могут попасть два и более изделий с абсолютно одинаковыми характеристиками. Следовательно, и в этом случае при обработке результатов выборки необходимо ориентироваться на методологию, используемую при повторном отборе.

При бесповторном отборе попавшая в выборку единица подвергается обследованию и в дальнейшей процедуре отбора не участвует. Такой отбор целесообразен и практически возможен в тех случаях, когда объем генеральной совокупности четко определен. Получаемые при этом результаты, как правило, являются более точными по сравнению с результатами, основанными на повторной выборке.

Как уже отмечалось выше, выборочное наблюдение всегда связано с определенными ошибками получаемых характеристик. Эти ошибки называются ошибками репрезентативности (представительности).

Ошибки репрезентативности обусловлены тем обстоятельством, что выборочная совокупность не может по всем параметрам в точности воспроизвести совокупность генеральную. Получаемые расхождения, или ошибки репрезентативности, позволяют заключить, в какой степени попавшие в выборку единицы могут представлять всю генеральную совокупность. При этом следует различать систематические и случайные ошибки репрезентативности.

Систематические ошибки репрезентативности связаны с нарушением принципов формирования выборочной совокупности. Например, вследствие каких-либо причин, связанных с организацией отбора, в выборку попали единицы, характеризующиеся несколько большими или, наоборот, несколько меньшими по сравнению с другими единицами значениями наблюдаемых признаков. В этом случае и рассчитанные выборочные характеристики будут завышенными или заниженными.

Случайные ошибки репрезентативности обусловлены действием случайных факторов, не содержащих каких-либо элементов системности в направлении воздействия па рассчитываемые выборочные характеристики. Но даже при строгом соблюдении всех принципов формирования выборочной совокупности выборочные и генеральные характеристики будут несколько различаться. Получаемые случайные ошибки могут быть статистически оценены и учтены при распространении результатов выборочного наблюдения на всю генеральную совокупность. Оценка ошибок выборочного наблюдения основана на теоремах теории вероятностей.

При дальнейшем рассмотрении теории и методов выборочного наблюдения в данной главе используются следующие общепринятые условные обозначения:

• • ЛГ— объем (число единиц) генеральной совокупности;
• • п — объем (число единиц) выборочной совокупности;
• • х — генеральная средняя, т. е. среднее значение изучаемого признака по генеральной совокупности (средняя прибыль, средняя величина активов, средняя численность работников предприятия и т. п.);
• • х — выборочная средняя, т. е. среднее значение изучаемого признака по выборочной совокупности;
• • М — численность единиц генеральной совокупности, обладающих определенным вариантом или вариантами изучаемого признака (численность городского или сельского населения, количество бракованных изделий, число нерентабельных предприятий и т. п.);
• • р — генеральная доля, т. е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, во всей генеральной совокупности (доля городского населения в общей численности населения, доля бракованной продукции в общем выпуске, доля нерентабельных предприятий в общей численности предприятий и т. п.);

м

определяется как —;

Л?

• • т — численность единиц выборочной совокупности, обладающих определенным вариантом или вариантами изучаемого признака;
• • хю — выборочная доля, т. е. доля единиц, обладающих определенным вариантом или вариантами изучаемого признака, i! выборочной совокупности; определяется как —;

п

• • р — средняя ошибка выборки;
• • Д — предельная ошибка выборки.

Ошибка выборки или отклонение выборочной средней от средней генеральной находится в прямой зависимости от дисперсии изучаемого признака в генеральной совокупности и в обратной зависимости от объема выборки. Таким образом, среднюю ошибку выборки можно представить как.

При проведении выборочного наблюдения дисперсия изучаемого признака в генеральной совокупности, как правило, не известна. В то же время между генеральной дисперсией и средней из всех возможных выборочных дисперсий существует следующее соотношение:

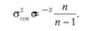
В связи с тем, что на практике в большинстве случаев из генеральной совокупности в определенный момент времени производится только одна выборка, дисперсия изучаемого признака по этой выборке и используется при расчете ошибки. Учитывая, что при достаточно большом объеме выборки отношение п/{п — 1) близко к 1, формула средней ошибки повторной выборки принимает следующий вид:

где о2 — дисперсия изучаемого признака по выборочной совокупности.

При определении возможных границ значений характеристик генеральной совокупности рассчитывается предельная ошибка выборки, которая зависит от величины ее средней ошибки и уровня вероятности, с которым гарантируется, что генеральная средняя не выйдет за указанные границы. Согласно теореме А. М. Ляпунова вероятность той или иной величины предельной ошибки при достаточно большом объеме выборочной совокупности подчиняется нормальному закону распределения и может быть определена на основе интеграла Лапласа.

Значения интеграла Лапласа при различных величинах переменной I табулированы и представлены в статистических справочниках. При обобщении результатов выборочного наблюдения наиболее часто используются следующие уровни вероятности и соответствующие им значения I:

Р…0,683 0,950 0,954 0,997.

г…1 1,96 2 3.

Например, если при расчете предельной ошибки выборки используется значение I = 2, то с вероятностью 0,954 можно утверждать, что расхождение между выборочной средней и генеральной средней не превысит двукратной величины средней ошибки выборки.

Теоретической основой для определения границ генеральной доли, т. е. доли единиц, обладающих тем или иным вариантом признака, является теорема Вернули. Согласно данной теореме вероятность получения сколь угодно малого расхождения между выборочной долей и генеральной долей при достаточно большом объеме выборки будет стремиться к единице. С учетом того, что вероятность расхождения между выборочной и генеральной долями подчиняется нормальному закону распределения, эта вероятность также определяется по функции /•" (?) при заданном значении ?.

Процесс подготовки н проведения выборочного наблюдения включает в себя ряд последовательных этапов:

• 1) определение цели обследования;
• 2) установление границ генеральной совокупности;
• 3) составление программы наблюдения и программы разработки данных;
• 4) определение вида выборки, процента отбора и метода отбора;
• 5) отбор и регистрация наблюдаемых признаков у отобранных единиц;
• 6) расчет выборочных характеристик и их ошибок;
• 7) распространение полученных результатов на генеральную совокупность.

В зависимости от состава и структуры генеральной совокупности выбирается вид выборки или способ отбора. К наиболее распространенным на практике видам относятся:

• • собственно-случайная (простая случайная) выборка;
• • механическая (систематическая) выборка;
• • типическая (стратифицированная, расслоенная) выборка;
• • серийная (гнездовая) выборка.

Отбор единиц из генеральной совокупности может быть комбинированным, многоступенчатым и многофазным.

Комбинированный отбор предполагает объединение нескольких видов выборки. Так, можно комбинировать типическую и серийную, серийную и собственно-случайную выборки. Ошибка такой выборки определяется ступенчатостью отбора.

Многоступенчатым называется отбор, при котором из генеральной совокупности сначала извлекаются укрупненные группы, потом более мелкие и так до тех пор, пока не будут отобраны тс единицы, которые подвергаются обследованию.

Многофазная выборка в отличие от многоступенчатой предполагает сохранение одной и той же единицы отбора на всех этапах его проведения; при этом отобранные на каждой стадии единицы подвергаются обследованию, каждый раз по более расширенной программе.