Численные методы решения жестких систем обыкновенных дифференциальных уравнений.
Семейства методов Рунге — Кутты и Розенброка

На каждой стадии метода решается система линейных уравнений с неизвестными к, и матрицей Е — /ту, J. Особый интерес представляют методы, у которых все диагональные коэффициенты в новом наборе у равны между собой (методы Розенброка — Ваннера), так что требуется лишь одно L[/-разложение на каждом шаге по времени для решения систем линейных уравнений. Рассмотрение методов этого семейства обычно… Читать ещё >
Численные методы решения жестких систем обыкновенных дифференциальных уравнений. Семейства методов Рунге — Кутты и Розенброка (реферат, курсовая, диплом, контрольная)
Рассмотрим другие методы для численного решения как линейных жестких систем ОДУ вида (6.1), так и нелинейных систем общего вида.

и автономных ЖС ОДУ[1]
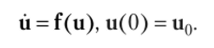
Из соображений устойчивости метода предпочтение естественно отдать неявным методам. Простейшими из них являются следующие.
1. Неявный метод Эйлера (приведем его вид для случая автономной ЖС ОДУ, в случае неавтономной системы формулы очевидны):
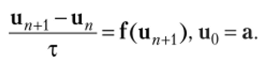
2. Метод трапеций.

3. Метод прямоугольников (правило средней точки).

гттг f — ^n+ _ UW+1 ^ UH.
где c,/+i/2 — - «u"+i/2 ~ 2 '.
Среди одношаговых методов для решения жестких систем наиболее известны методы Рунге — Кутты. Все приведенные выше в данном параграфе формулы можно рассматривать как частные случаи неявных однои двухстадийных методов из этого семейства (см. ниже). Не останавливаясь на получении коэффициентов, выпишем наиболее известные из формул Рунге — Кутты, используя таблицу Бутчера.
Отметим, что в отличие от рассматриваемых выше явных методов, при использовании неявных схем Рунге — Кутты матрица коэффициентов метода в таблице Бутчера заполненная, и для определения вспомогательных векторов, входящих в функцию приращения, приходится решать систему нелинейных алгебраических уравнений.
1. Методы Гаусса соответственно 2-го, 4-го и 6-го порядков представлены в табл. 6.1—6.3. Первый метод совпадает с правилом средней точки. Второй метод (4-го порядка) носит название метода Хаммера — Холлинсворта.
Таблица 6.2 Таблица Бутчера для метода Гаусса 4-го порядка.
½. | ½. |
Таблица 6.1 Таблица Бутчера для метода Гаусса 2-го порядка.
½. | ½. |
Таблица 63
Таблица Бутчера для метода Гаусса 6-го порядка.
2. Методы Радо ПА 1-го, 3-го и 5-го порядков представлены соответственно в табл. 6.4—6.6. Метод 1-го порядка является неявным методом Эйлера.
Таблица 6.4 Таблица 6.5
Таблица Бутчера Таблица Бутчера для метода Радо i-го порядка для метода Радо 3-го порядка.
1/3. | 5/12. | — 1/12. |
¾. | ¼. | |
¾. | ¼. |
Таблица Бутчера для метода Гаусса 5-го порядка.
| 88−7ч/б. | 296 — 169>/б 1800. | — 2 + Зл/б 225. |
4 + Тб 10. | 296+ 169Тб 1800. | 88 + 76 360. |
|
i6-Ve. |
|
| |
|
|
|
Таблица 6.7 Таблица 6.8
Таблица Бутчера для метода Таблица Бутчера для метода Лобатто ША 2-го порядка Лобатто ША 4-го порядка.
3. Методы Лобатто ША 2-го, 4-го и 6-го порядков точности см. в табл. 6.7— 6.9 соответственно. Очевидно, что метод 2-го порядка точности является неявным методом трапеций.
½. | ½. | ½. | 5/24. | 1/3. | — 1/24. | |
½. | ½. | 1/6. | 2/3. | 1/6. | ||
1/6. | 2/3. | 1/6. |
Таблица 6.9
Таблица Бутчера для метода Лобатто ША 6-го порядка.
| iiWs. |
|
|
|
|
|
| 25 + [э 120. |
|
1/12. | 5/12. | 5/12. | 1/12. | |
1/12. | 5/12. | 5/12. | 1/12. |
Рассмотрим теперь, как строится функция устойчивости для методов Рунге — Кутты[2]. Как уже отмечалось выше, при построении функции устойчивости рассматривается модельное уравнение (уравнение Далквиста) вида.
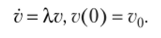
В этом уравнении скалярный параметр — элемент спектра матрицы Якоби исходной жесткой задачи. Вообще говоря, среди собственных чисел нашей ЖС ОДУ могут встретиться пары комплексно-сопряженных, поэтому и матрица перехода в базис из собственных векторов тоже комплексная. Таким образом, модельное уравнение Далквиста — линейное комплекснозначное дифференциальное уравнение с действительным аргументом.
Запишем метод Рунге — Кутты для уравнения Далквиста в обшей форме (см. гл. 5, в частности табл. 5.1 и формулы (5.4)) с использованием новых переменных Y:

Приведенные выше формулы можно рассматривать как систему линейных уравнений относительно новых переменных Yv …, Yk> vn+{ следующего вида:

Нам необходимо выразить vri+{ через vrr Для этого воспользуемся правилом Крамера. Ответ можно записать в следующей форме:

где E — единичная матрица размера s х s; А — матрица коэффициентов входящая в таблицу Бутчера; е — единичный вектор размерности s (столбец); Ъг — строка коэффициентов bv входящая в таблицу Бутчера; 5 — число стадий метода Рунге — Кутты.
Условием устойчивости метода будет.

Одноитерационные методы Розенброка. X. Розенброком был предложен класс неявных методов, в котором не решается система нелинейных уравнений.
Для иллюстрации построения класса методов Розенброка рассмотрим автономное дифференциальное уравнение у' = /(г/).
Рассмотрение методов этого семейства обычно начинают с диагонально-неявного метода Рунге — Кутты (ДНРК). Диагонально-неявными называются такие методы, в которых матрица коэффициентов в таблице Бутчера — нижняя треугольная. Для облегчения дальнейшей записи все вспомогательные величины k сразу умножим на величину шага сетки:

Линеаризация ДНРК дает систему.

Эта линеаризация ДНРК эквивалентна применению одной ньютоновской итерации с нулевыми начальными значениями для всех k на каждой стадии в ДНРК. Вместо продолжения итераций до сходимости можно рассмотреть последние формулы как новый класс методов. Такую схему иногда называют методом с одной итерацией, имея в виду, что вычисление обратной матрицы сравнимо по количеству арифметических операций с одной итерацией метода Ньютона. Преимущество методов типа Розенброка перед прочими классами численных методов Ж С ОДУ заключается в том, что для определения решения на верхнем временном слое необходимо решать уже линейную систему алгебраических уравнений.
Существенный вычислительный выигрыш получается при замене матриц Якоби f'(gj) на J = /'(г/0), так что метод требует ее вычисления только один раз (методы Розенброка — Ваннера).
Мы получим больше свободы, введя добавочные линейные комбинации членов Jk, в последнюю систему. Правда, как правило, такое расширение поля коэффициентов приводит к некоторому ухудшению свойств устойчивости.
Определение 6.5. s-Стадийный метод Розенброка задается формулами.
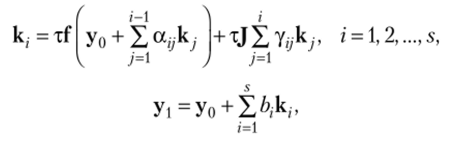
где а, у, Уу, — определяющие коэффициенты метода и J = /'(Уо) —
На каждой стадии метода решается система линейных уравнений с неизвестными к, и матрицей Е — /ту, J. Особый интерес представляют методы, у которых все диагональные коэффициенты в новом наборе у равны между собой (методы Розенброка — Ваннера), так что требуется лишь одно L[/-разложение на каждом шаге по времени для решения систем линейных уравнений.
Для неавтономных задач уравнение у' = f (x, у) может быть преобразовано в автономную систему ОДУ добавлением уравнения х' = 1.
Исключая компоненты, соответствующие переменной х, получим 

Отметим, что при использовании методов Рунге — Кутты все определяющие коэффициенты метода являются действительными числами. Произвольные правые части систем ОДУ могут не быть аналитическими функциями своих аргументов. Поэтому коэффициенты, входящие под знаки функции в качестве множителей в аргументах, следует выбирать только вещественными. Вне функций стоят коэффициенты у. Эти коэффициенты входят в линейную алгебраическую систему, которую всегда можно решать и при комплексных коэффициентах. Поскольку численное решение должно быть вещественным, то после решения линейной системы исключаем мнимую часть решения.
Одностадийную схему можно записать в виде.

Для обеспечения порядка аппроксимации не ниже первого уже выбрано 6=1. Такой метод называется методом CROS, для него доказаны следующие утверждения.
Схема имеет точность 0(т2), если Rey = а{ = ½.
Эта схема Д-устойчива, если Rey > 1 /2.
В простейшем случае для автономной системы уравнений метод Розенброка типа CROS может быть записан в действительных переменных. Тогда получаем[3]:

Здесь В = -^-(и") — матрица, постоянная на данном шаге по времени.
Эи Параметры а, 6, с подбираются таким образом, чтобы обеспечить максимально возможный порядок точности. Например, для схемы порядка 3 аппроксимации получим у = 1,077; у2 = - 0,372; а = -0,577.
- [1] См. также работы: Хайрер Э., Нерсетт С., Ваннер Г. Указ, соч.; Хайрер Э. у Баннер Г. Указ, соч.; Деккер К., Вервер Я. Устойчивость методов Рунге — Кутты для жестких нелинейных дифференциальных уравнений. М.: Мир, 1988; Вычислительные процессы и системы.Вып. 8 / под ред. Г. И. Марчука. М.: Наука, 1991; Ракитский Ю. В., Устинов С. А/., Черно-руцкий И. Г. Численные методы решения жестких систем обыкновенных дифференциальныхуравнений. М.: Наука, 1979.
- [2] Деккер К., Вервер Я. Указ. соч.
- [3] Федоренко Р. П. Указ. соч.