Логарифмический вычет и принцип аргумента

Рассмотрим многозначную функцию.

Во всех точках 2, в которых f (z) аналитична и не обращается в нуль, Ln f (z) будет многозначной аналитической функцией. Каждая ее ветвь, получаемая выбором конкретного значения к, является однозначной аналитической функцией в некоторой окрестности точки 2. Эти ветви отличаются на постоянное слагаемое, и поэтому их производные совпадают. Производная каждой ветви функции Ln }(z). равная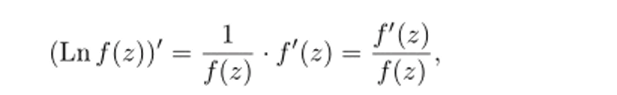

называется логарифмической производной функции f (z) она является однозначной аналитической функцией всюду, за исключением особых точек и нулей функции f (z). Вычет функции f'(z)/f (z) (т.е. вычет логарифмической производной функции f (z)) в точке Zq называется логарифмическим вычетом функции f (z) в точке zq.

Теорема 29.1. Если zq — нуль кратности п аналитической функции f (z). то логарифмический вычет функции f (z) в точке Zo равен п; если Zq — полюс порядка р, то логарифмический вычет равен —р.

Доказательство. Пусть zo — нуль кратности п. Тогда f (z) представима в виде (см. (23.2)) f (z) = (z — zo)ⁿip (z), где tp (z) — аналитическая функция в некоторой окрестности точки Zq и.

ф 0. Отсюда.

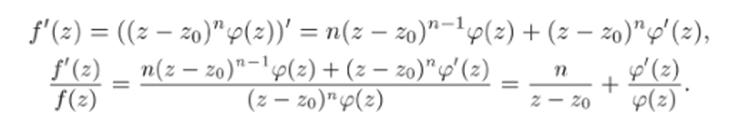
Так как.

Ф 0, то функция 4t{z)/

является аналитической в некоторой окрестности точки zq и, следовательно, раскладывается в этой окрестности в ряд Тейлора:

Поэтому главная часть лорановского разложения функции f'(z)/f (z) состоит из единственного члена —-—, а коэффициент с~ при.

Z Zo

(z — zo)^-1 равен n. Следовательно, (см. (27.4)).

Пусть теперь zо — полюс порядка р функции f (z). Тогда функция y (z) = 1 /f (z) имеет в точке zo нуль порядка р. Согласно доказанному выше, resz₀W/я) = Р- Так как Lnp = Ln (l//) = - Ln /, то.

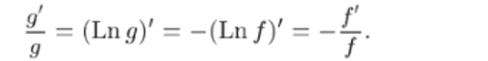
Отсюда и из определения вычета (27.1) получаем.

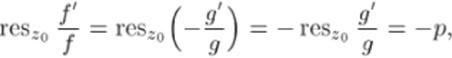
что и требовалось доказать.

В следующих далее теоремах будет установлена связь между количеством нулей и полюсов функции f (z) внутри области и поведением f (z) на границе области. При подсчете количества нулей и полюсов мы примем следующее соглашение: каждый пуль и полюс считается столько раз, каков его порядок.

Теорема 29.2 (теорема о логарифмическом вычете). Пусть Г — замкнутый контур, лежащий в области аналитичности функции f (z). Пусть, далее, f (z) аполитична во всех точках внутри Г, за

исключением коне чного числа полюсов, и не имеет на Г ни пулей, ж/ полюсов. Тогда

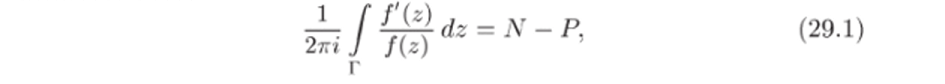
где N — число нулей, а Р — число полюсов функции f (z) внутри Г, подсчитанных с учетом кратности; обход контура Г предполагается таким, что точки, леэ! сащие внутри Г, остаются слева.

Доказательство. Обозначим 6'(г) = f'(z)/f (z). Поскольку на Г функция f (z) не имеет ни нулей, ни полюсов, то функция G (z) аналитична во всех точках контура Г. Внутри Г функция G (z) имеет лишь конечное число особых точек, являющихся нулями и полюсами функции f (z). Значит, к функции G (z) применима теорема 27.1 о вычетах, согласно которой.

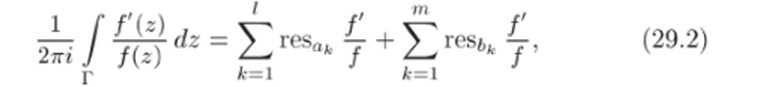
где а*, к = 1,2,…,/ и 6*, к = 1,2,…, га, — соответственно нули и полюсы функции G (z). В силу теоремы 29.1.

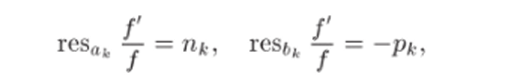
где Пк и Рк — порядки нуля ец. и полюса 6* соответственно. Подсчитывая нули и полюсы с учетом кратности, получим.

Подставляя эти равенства в (29.2), приходим к соотношению (29.1), что нам и требовалось.

Величина в левой части (29.1) называется логарифмическим вычетом функции f (z) относительно контура Г; этим и объясняется название теоремы 29.2. Мы покажем, что эта величина имеет геометрический смысл и, следовательно, теорема 29.2 выражает определенное геометрическое свойство отображения, осуществляемого функцией W = f (z).

Зафиксируем на Г произвольную точку го (рис. 51. а). Ей соответствует точка Wo = /(г₀) плоскости переменного w (рис. 51, б). Если точка 2 движется по Г начиная от го, то соответствующая точка w = /(г) будет описывать некоторую траекторию С в плоскости w начиная от точки wo. При возвращении точки г в го точка w придет в wo. Поэтому путь С также является замкнутым (хотя, возможно, будет иметь самопересечения). Возьмем In w₀ = In wq + i arg wq.

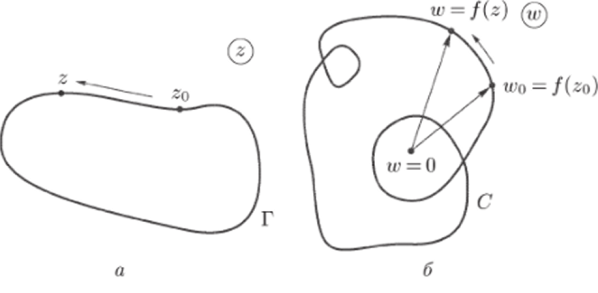
Рис. 51.

главное значение логарифма числа WoКаждой точке w € С соответствует бесконечно много значений аргумента Argiv = argw + Ътк, к = 0, ±1, ±2,… Но мы выберем такое из них, чтобы при движении по С аргумент числа w менялся непрерывно. Это значение аргумента обозначим (p (w). При возвращении в wq после обхода пути С значение.

будет приближаться к некотором}' числу <^(wo), которое не обязано совпадать с исходным значением arg од • Таким образом, при обходе С аргумент числа w = f (z) получит некоторое приращение Др arg / = ip (wo) — arg w₀. Это приращение, очевидно, равно числу оборотов вокруг точки w = 0, которое сделает вектор w при обходе точкой w пути С, умноженному на 2тг (при каждом обороте аргумент изменяется на 2тг). На рис. 51, 6 число оборотов равно 2.

Теорема 29.3 (принцип аргумента). Пусть Г — зеимкпутый контур, лежащий в области аналитичности функции f (z). Пусть, далее, f (z) аполитична во всех точках внутри Г, за исключением конечного числа полюсов, и не имеет на Г ни пулей, ни полюсов. Тогда приращение аргумента числа w = f (z) при обходе точкой z конту- 7hi Г ]И1впо 27 г (Л^г — Р):

где N и Р — число нулей и полюсов фгункции f (z) внутри Г, взятых с учетом, кратности. Другими словами, число оборотов вектора /(г), сделанных им при обходе точкой z контура Г, равно N — Р.

Доказательство. Пусть, как и выше, ip (w) — непрерывно изменяющийся аргумент числа w. Рассмотрим функцию Ф (г) = = Inf (z) + i

В окрестности каждой точки г € Г функция Ф (г) совпадает с одной из ветвей многозначной аналитической функции Ln f (z) = In f (z) + i (argf (z) + 2тгЛг). Поэтому.

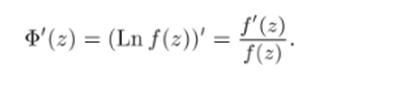
Следовательно, непрерывная на Г функция Ф(z) является первообразной функции f'(z)/f (z). По формуле Ныотона-Лейбница.

где АФ (г) — приращение функции Ф (г) = In f{z) + ip (f (z)) при полном обходе точкой 2 контура Г. Поскольку In f (z) является однозначной непрерывной функцией на Г, то при возвращении точки z it zq этот логарифм примет начальное значение In f (zo) и его приращение будет равно нулю. Когда г проходит контур Г, соответствующая точка w = f (z) проходит путь С. Поэтому приращение функции p{f (z)) равно Ар = p (wo) — arg wo = Ар arg/. Таким образом,.

aside class="viderzhka__img" itemscope itemtype="http://schema.org/ImageObject">

Из этого равенства, а также из (29.4) и (29.1) получаем что и требовалось доказать.

Пусть, например, Г — достаточно малая окружность, охватывающая нуль кратности п функции f (z). Тогда N = п, Р = 0. Согласно теореме 29.3, при однократном обходе точкой z окружности Г вектор f (z) совершит п оборотов вокруг начала координат против часовой стрелки. Если же Г охватывает полюс порядка р (т.е. N = 0, Р = р), то вектор f (z) совершит р оборотов по часовой стрелке.

Полезным применением признака аргумента, является следующая теорема.

Т е о р е м, а 29.4 (теорема Руше). Пусть функции f (z) и g (z) аналитичны во всех точках замкнутого контура Г и внутри него иf (z) > | y (z) на Г. Тогда их сумма F (z) = f (z) + g (z) имеет внутри Г столько же нулей с учетом их кратности, что и f (z).

Доказательство. Покажем вначале, что функции f (z) и F (z) не имеют нулей на Г. Для любых комплексных чисел а и Ь справедливо неравенство |о + 6| ^ а — |6|. Оно следует из неравенства треугольника:

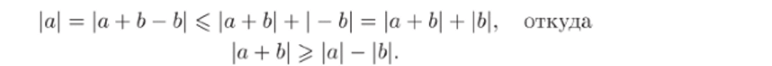
Используя это неравенство и условие теоремы, получим.

для всех z € Г. Значит. f (z) и F (z) не обращаются в нуль на Г, и к ним можно применить принцип аргумента. Так как f (z) ф 0 на Г. то.

При умножении комплексных чисел их аргументы складываются. Отсюда следует, что.

q{_z).

По условию теоремы, < 1 для всех точек z € Г. Поэтому если обозначить w (z) = 1 + тт-т? то w — 11 = |тт-т < АЭто неравенство.

/(*) I f (z)

означает, что при обходе точкой г контура Г точка w будет двигаться.

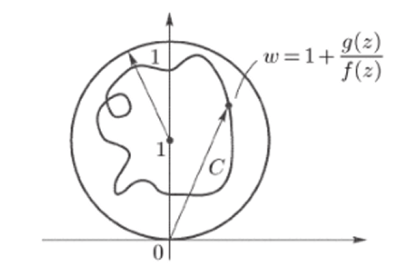
но замкнутой траектории, лежащей внутри круга w — 1| < 1 (рис. 52). Следовательно, вектор w не сделает ни одного оборота вокруг точки w = = 0; аргумент </?(ш) числа w вернется к начальному значению, и его приращение Дг arg (l + g/f) будет равно 0.

Итак, Д г arg (/ + д) = Д г arg /. Применяя к каждой из функций / + д и / равенство (29.3) сР = 0 (функ- ^^ис* ^ ции аналитичны, и полюсов нет),.

приходим к тому, что эти функции имеют внутри Г одинаковое число нулей. Теорема Руше доказана.

Теорема 29.4 иногда позволяет определить число нулей функции в заданной области.

П р и м е р 29.5. Определить число корней уравнения z^s — 42⁵ + + z² — 1 = 0 в круге |^| < 1.

Р е ш е и и е. Возьмем /(г) = —4z⁵, g (z) = z⁸ + z² - 1. В точках окружности z = 1 имеем.

Таким образом, f (z) > g (z) на окружности Г = {z = 1}. По теореме Руше функция /(г) + g (z) = z^H — 4г⁵ + z² — 1 имеет в круге z < 1 столько же нулей, сколько и функция f (z) = —4z^r>. Но f (z) обращается в нуль только в точке z = 0, являющейся нулем функции f (z) пятого порядка. Следовательно, и функция f (z) + g (z) имеет в круге z < 1 пять нулей (с учетом кратности).

Важным применением теоремы Руше является простое доказательство с ее помощью так называемой основной теоремы алгебры.

Теорема 29. G (основная теорема алгебры). Любой многочлен п-й степени P_n(z) — + aⁿ~^l +… + а_п, «о Ф 0, имеет о плос

кости С комплексного переменного z в точности п нулей с учетом их кратности.

Доказательство. Запишем P_n(z) в виде P_n(z) = f (z) + y (z), где f{z) = aozⁿ, g (z) = azⁿ~^l + Так как.

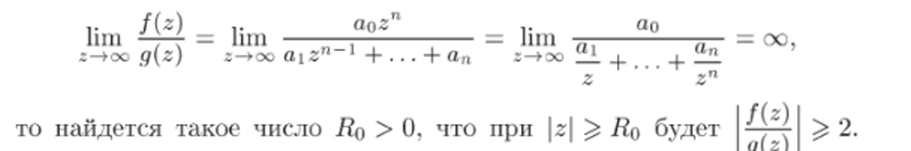
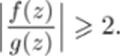
Возьмем произвольное R > R_{). Тогда при z = R получим f{z) ^ ^ '2y (z) > y (z). По теореме Руше P_n(z) имеет в круге z < R столько же нулей, сколько и функция f (z) = aozⁿ. Эта функция имеет нуль кратности п в начале координат, т. е., с учетом кратности, п нулей. Таким образом, в любом круге z < R сколь угодно большого радиуса R > Ло многочлен P_n(z) имеет ровно п нулей. Значит, и во всей комплексной плоскости С их будет в точности п.