Задачи и упражнения

11.1.1 Накачка четырехуровневой квантовой системы.

Накачка квантовой системы может происходить по четырехуровневой схеме, например, в газовом лазере. Возбуждение осуществляется с уровня / на уровень 4. Инверсия населенностей образуется между средними уровнями 3 и 2. Вероятности переходов с уровня 4 на уровень 3 и с уровня 2 на уровень / достаточно велики, так что уровни 4 и 2 можно всегда считать пустыми (рис. 1.3). Кинетические уравнения для такой системы обычно записываются в виде где W— число частиц, попадающих на уровень 3 за счет накачки в единицу времени; — число частиц на уровне 3 (напомним, что число частиц на уровне 2 равно л₂ = 0);

В₀— константа, зависящая от частоты; N— число фотонов в типе колебаний резонатора лазера; т— время спонтанного излучения; т, — время жизни фотонов в резонаторе; е_с — вероятность того, что фотоны, образующиеся в результате спонтанного распада, попадают в рассматриваемый тип колебаний.

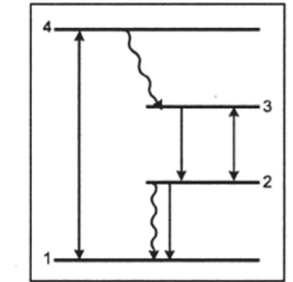
Рис. 1.3. Четырехуровневая система Накачка происходит с уровня 1 на уровень 4. Рабочий переход осуществляется между уровнями 3 и 2. Прямыми стрелками показаны излучательные переходы, а волнистыми — безызлучательные.

• 1. Определить В_с и е_с и показать, что В_с =е_с/т, т. е. показать, что кинетическое уравнение для числа фотонов можно записать в виде dN Idl = B_cn{N +1) — N/t_/# .
• 2. Написать явный вид выражений В_с и е_с для лоренцевой формы линии люминесценции активного вещества.

Решение Для вычисления величины В_с рассмотрим изменение числа фотонов в типе колебаний за счет индуцированных переходов. Если p_v— спектральная плотность энергии поля, V— объем кристалла, то изменение числа фотонов в типе колебаний в единицу времени за счет индуцированных переходов будет

Р V

Учтем, что N-——, а также соотношения между коэффициентами Z?₃₂(v) и В_гЛ). hv

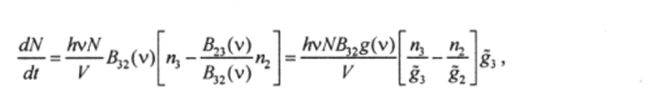
Тогда.

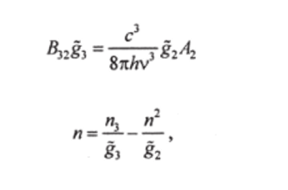
где g, — кратности вырождения уровней, a g (v) — форм-фактор линии. Учитывая, что и вводя обозначение получим

Для лорениевой формы линии имеем 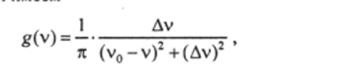где Ду —полуширина линии. Тогда 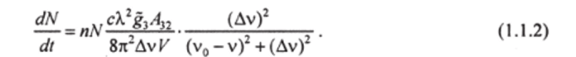Из равенства (1.1.2) видно, что и, в частности, для вершины линии Выражения (1.1.3) и (1.1.4) для константы B_t получены в предположении, что на обоих рабочих уровнях число активных частиц отлично от нуля. Согласно же условиям задачи п_г = 0, т. е. п — «jg,. Подставляя это выражение в (1.1.1), получаем вместо (1.1.3) и (1.1.4).

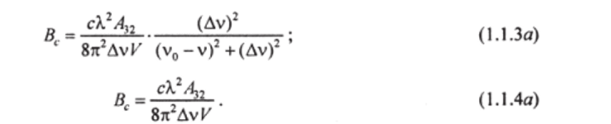
Отметим, что в формулы (1.1.3) и (1.1.4) входит длина волны излучения в веществе. Если <�п_г— показатель преломления кристалла, то.

где Х₀ —длина волны излучения в вакууме.

Вычислим теперь независимым образом г_с. Предположим, что все поверхности лазерного кристалла идеально отражающие, т. е. сам кристалл представляет собой резонатор без потерь. Тогда в частотном интервале от v до v + cfv в кристалле с показателем преломления п, возбуждается число типов колебаний:

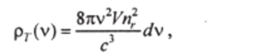
где V— объем кристалла.

Число спонтанных распадов уровня 3 в единицу времени составляет п_}/ т, причем частное распределение излучаемых фотонов определяется формой линии люминесценции активного вещества, и в частотный интервал от v до у + сЛ' попадает rt)g (v)dv/т фотонов.

Очевидно, число фотонов, попадающих в один тип колебаний, равно Следовательно,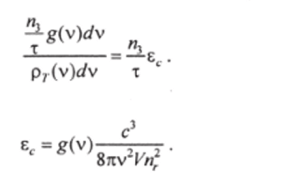

Для лорснцевой формы линии люминесценции*.

_с2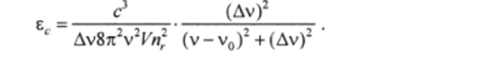

Учитывая, что —т—г = Х² и то, что для рассматриваемой четырехуровневой системы.

v я;

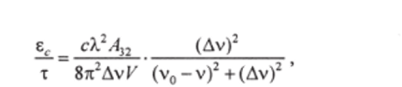
Ау_г = 1/т, получаем т. е. выражение е_с/х совпадает с выражением (1.1.3а). Это позволяет записать кинетическое уравнение для числа фотонов в виде.

|1.2.| Накачка лазерного кристалла Рассмотреть накачку лазерного кристалла источником интенсивностью /₀(Х") в единичном интервале длин волн. Кристалл выполнен в виде прямоугольного параллелепипеда длиной L с квадратным сечением, длина которого равна а (рис. 1.4). Зеркала нанесены прямо на грани кристалла (штриховка).

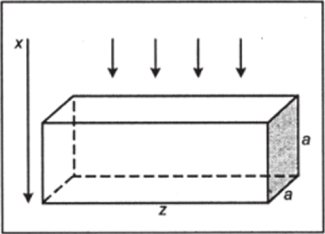
Рис. 1.4. Схема накачки лазерного кристалла.

Излучение источника накачки падает перпендикулярно к грани кристалла в направлении оси х. Коэффициент поглощения излучения в кристалле А (ХД квантовая эффективность ц (Х"). Источник накачки считать достаточно узкополосным, т. е. в пределах ширины спек;

тра источника величины А (Х"), itfX*) и Х" можно считать постоянным: А (Х") = к_п п (Х_и) =.

• 1. Оценить пороговую мощность источника накачки, считая, что поглощение в кристалле невелико и не влияет на интенсивность проходящего через кристалл излучения.
• 2. Учтя изменение интенсивности сигнала накачки за счет поглощения в кристалле, определить предельную толщину кристалла, для которой накачка еще эффективна.

В этом случае считать, что /₀ = J /(Х_н)с/Х" = 26,8 Вт/см², где интегрирование происходит по всему спектру источника накачки.

3. Кроме того, при оценках использовать следующие данные: п, = 1,4, п — Зх10¹⁸ см'³,.

к_р=см~¹, — 0,64 мкм, ц, а1. Ширина линии люминесценции (при Т = 290 К) составляет 2Ду=1.1см', длина параллелепипеда L^m 1,2 см, а сторона квадрата а = 0,1 см, коэффициент отражения зеркал - 0,9, длина волны излучения X *• 0,7 мкм.

Решение Оценим мощность источника накачки, поглощаемую в единице объема кристалла.

За счет поглощения в кристалле интенсивность падающего на грань кристалла излучения источника накачки уменьшается по закону.

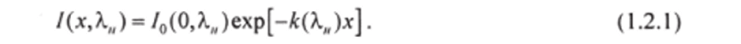
Изменение интенсивности на элементе пути dx в плоскости д, кристалла равно.

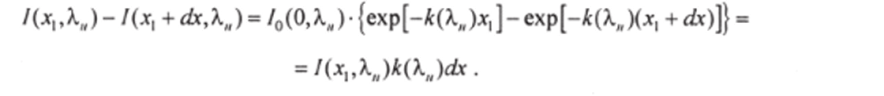
Таким образом, мощность, поглощаемая в единице объема и интервале длин волн от X до X + с/Х, равна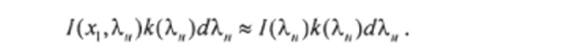

Из этого количества только ц-я часть идет на создание инверсной населенности, т. е. полезная мощность равна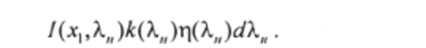

Энергия поглощенного фотона h = Ис / Х".

Считая, что один поглощенный фотон приводит к появлению одной возбужденной частицы на верхнем рабочем уровне, получаем, что число п' частиц, возбуждаемых в единице объема в единицу времени за счет поглощения излучения во всей ширине источника, равно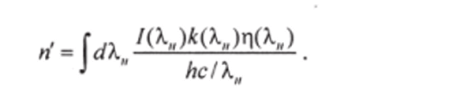

Поскольку Х (Х"), п (Х"), Х" в пределах спектра излучения источника мало изменяются, выносим их из-под знака интеграла, получая.

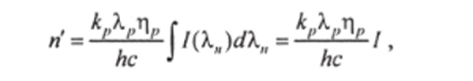
2' где 1 — интегральная интенсивность по всему спектру источника накачки:

Число частиц в единице объема, уходящих с уровня в единицу времени за счет спонтанных переходов на пороге генерации, равно п_Ш1р/ (рассматривается пороговое значение накачки). Очевидно, должно выполняться равенство п' = п,_вг / и, следовательно, т. е. пороговая интенсивность

При отсутствии вырождения для лоренцевой формы линии.

Подставляя (1.2.3) в (1.2.2) и учитывая, что Л₃₂ = 1 / т_ап а длина волны излучения в кристалле X связана с длиной волны излучения в вакууме Хо соотношением.

имеем Для исходных данных задачи это дает 13,4 Вт/см². Поверхность кристалла, на которую падает поток S = La = 0,12 см², т. е. мощность падающего на кристалл излучения 1,2 Вт.

Предельная толщина а кристалла определится из условия, что при проникновении в глубь кристалла на расстояние о интенсивность падает настолько, что инверсная населенность становится меньше пороговой п < n_mv.

Если /₀ — начальная интенсивность, то а определится из условия 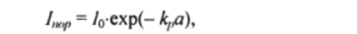где /_mft находят по формуле (1.2.4). Таким образом,.

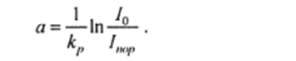
Для /₀ = 26,8 Вт / см²,1″_г = 13,4 Вт / см², используя исходные данные, получаем а * 0,7 см. [1.3.1 Добротность резонатора Рассчитать добротность Q, и время жизни фронта в резонаторе Фабри — Перо с плоскими зеркалами. Расстояние между зеркалами L = 1 м. В резонаторе возбуждается один основной тип колебаний ТЕМооу, образуемый двумя бегущими навстречу друг другу плоскими волнами (Х = 0,6мкм). Среда, заполняющая резонатор, слабо поглощающая (коэффициент поглощения р = 0,001 см^-1). Эти потери могут быть связаны с процессами рассеяния в среде, нерезонансного поглощения и т. д. Коэффициент отражения каждого из зеркал г. тр ~ 95%. Диаметр зеркал много больше диаметра светового пучка, так что дифракционными потерями можно пренебречь.

Решение Получим формулу для добротности типа колебаний открытого резонатора, учитывающую потери в зеркалах и в среде, заполняющей резонатор.

По определению добротности, если иук— энергия типа колебаний в резонаторе, то.

где щ_к — энергия типа колебаний в момент / = 0.

Из (1.3.1) следует, что энергия, теряемая за время dt, равна.

Рассматриваемый тип колебаний, как две волны, бегущих навстречу друг другу, причем энергия каждой из них равна ч_ТК/2. Потери каждой из волн на проход за счет поглощения в среде (РЛ"1).

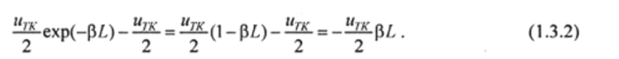
Потери для этой же волны на проход за счет пропускания зеркала.

Полные потери за один проход (т. е. за время = L! с) каждой из волн определяются суммой (1.3.2) и (1.3.2а). Энергия, теряемая каждой волной в среднем в единицу времени, а обеими волнами за время dt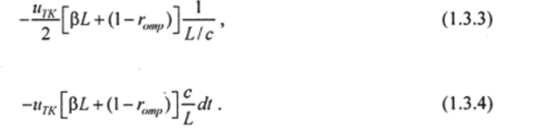

С другой стороны, выражение (1.3.4) должно совпадать с выражением (1.3.1а). Приравнивая их, получаем.

Подставляя значения параметров из условий задачи, находим Q_p — 7х Ю⁷, т, *2×10″ * с.