Полосопропускающие фильтры. 
Электроника

Полосопропускающий (или просто — полосовой) фильтр может быть выполнен в виде последовательного соединения двух фильтров — нижних частот (ФНЧ) и верхних частот (ФВЧ), характеристики которых подобраны так, что имеется перекрывающийся участок (рис. 3.33, а).

В зависимости от области используемых частот и требуемой избирательности полосовой фильтр может быть составлен из пассивных или активных LC- или ДС-фильтров нижних и верхних частот (с коэффициентами передачи фильтров Баттерворта, Бесселя или Чебышева). При этом характеристические сопротивления для LC-фильтров нижних и верхних частот должны быть одинаковы, а для ДС-фильтров необходимо взаимное влияние звеньев свести к минимуму, например разделив их усилительными элементами.

Так поступают, когда полоса пропускания Д/=/, -/" достаточно широка и сравнима со средней геометрической частотой:/_ср = 'iff, или если /"//" > 2. При /"//"—> 1 обычно применяют специальные полосовые фильтры.

Мостик Вина (рис. 3.33, б) является простейшим полосовым (?С-фильтром. Комплексный коэффициент передачи этого фильтра:

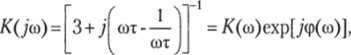
где К (ш) = [9 + (ют — 1/ют)'^,/2; т = RC; <�р (ю) = arctg [0,333 (ют — 1/шт)].

Особенность моста Вина — возникновение на частоте ш_р = 1 /RC максимума коэффициента передачи, своеобразного «квазирезонанса» (рис. 3.33, в). При этом К (ш_р) = 1/3; <�р (ю_р) = 0.

Пассивные полосовые ЙС-фильтры имеют очень малую избирательность и поэтому обычно применяются в сочетании с усилительными элементами, в составе активных фильтров.

Простейший пассивный полосовой 1С-фильтр для работы на высоких частотах — последовательный или параллельный колебательный контур, подробно рассмотренный ранее (см. п. 3.4).

Ширина полосы пропускания технически грамотно выполненного, с малыми потерями, Z. C-колебательного контура обычно не превышает нескольких процентов от резонансной частоты, и поэтому для выделения достаточно широкополосных сигналов приходится полосу пропускания расширять, что может быть достигнуто за счет введения дополнительного затухания в ЕС-контур путем его шунтирования резистором. Однако это ухудшает избирательность, так как крутизна спада при этом уменьшается.

Если полоса пропускания Д/должна быть широка, а крутизна спада коэффициента передачи за пределами полосы пропускания велика, то применяются полосовые ЕС-фильтры с более сложной схемой (рис. 3.33, г).

Элементы таких фильтров определяются по формулам:

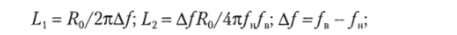
где й₀= VZA= VLjC) — характеристические сопроти влен ия.

На частотах ниже 100 кГц в настоящее время наиболее часто используют активные полосовые ЙС-фильтры с использованием частотно-зависимой отрицательной обратной связи.

В частности, на схеме рис. 3.33, д приведена схема узкополосного активного фильтра с использованием двойного Т-образного RC-моста. Передаточная характеристика такого фильтра:

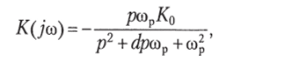
где d= 1/Q," = Дм/о)_р; Q,_K> — эквивалентная добротность фильтра; Дсо — полоса пропускания, определяемая на уровне 0,7й₀; со. — частота квазирезонанса фильтра.

Пассивные ЙС-элементы фильтра определяются путем выбора значений К₀= 1−10²; d< 0,1; со_р и емкости С₂ конденсатора С2, после чего определяются остальные элементы по формулам: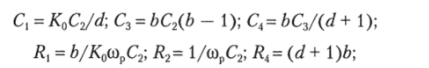

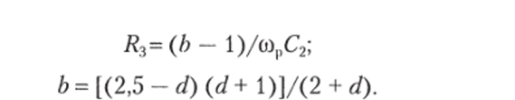
Схема узкополосного активного /?С-фильтра Баттерворта приведена на рис. 3.33, е. Коэффициент передачи этого фильтра:

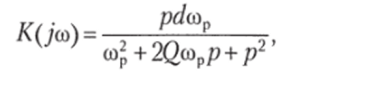
где d = 1 /Q (0_р — частота настройки. Я С-элементы, так же как и ранее, задаются значениями d< 0,1; К₀= 1−10² и емкостью С₂ конденсатора С2, после этого рассчитывают значения остальных элементов по формулам: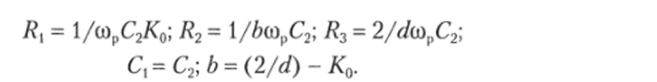

Узкополосные активные фильтры очень часто выполняются на основе гираторов. Одна из возможных схем выполнения гиратора, представляющая собой встреч но-параллельное включение двух операци;

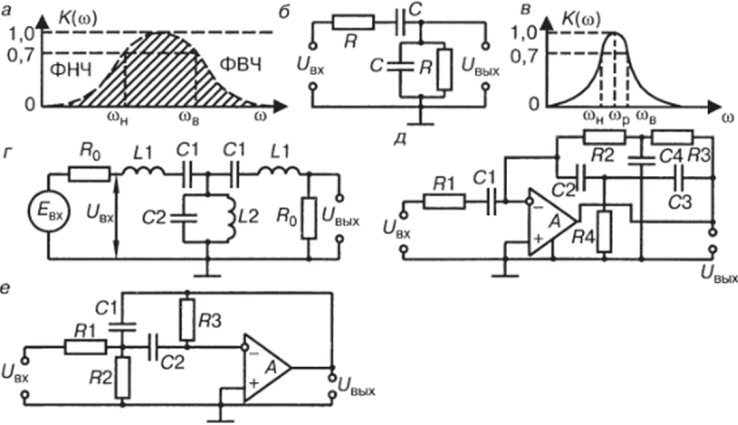
Рис. 3.33. Полосопропускающие фильтры: частотная характеристика полосопропускающего фильтра, составленного из фильтров нижних ФНЧ и верхних ФВЧ частот (а) простейший ЯС-фильтр^б); амплитудно-частотная характеристика узкополосного полосового фильтра и его полоса пропускания (в) пассивный LC-фильтр (г) активный фильтр с двойным Т-образным местом в цепи отрицательной обратной связи (д) активный фильтр с двухпетлевой цепью частотно-зависимой отрицательной обратной связи (е).

онных усилителей — инвертирующего -А и неинвертирующего +А, приведена на рис. 3.34, а.

Усилители должны иметь высокие входные и выходные сопротивления: Д,_х->~; R,

Уравнение передачи гиратора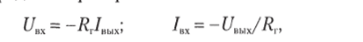

где R_r — сопротивление тирании, отображающее усилительные свойства используемых операционных усилителей.

Из этого уравнения можно найти входное сопротивление гиратора:

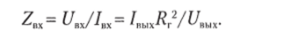
Но /_ВЫУН_ВЬ|Х= 1/Z", поэтому входное сопротивление гиратора определяется как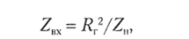

где Z" — сопротивление нагрузки на выходе гиратора.

Если, например, гиратор нагружен на конденсатор С", то его входное сопротивление имеет индуктивный характер:

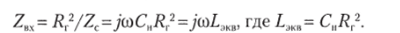
Поэтому, если на входе и выходе гиратора стоят конденсаторы С и С", получается активный фильтр, эквивалентный последовательному LC-контуру (рис. 3.34, б).

Схема гиратора менее чувствительная, чем предыдущая к изменениям параметров операционных усилителей и ДС-компонентов, приведена на рис. 3.34, в. Для этой схемы входное сопротивление:

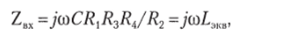
где = R_tR₃R_tC/R₂.

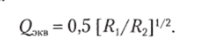
Для выполнения гиратора необязательно использовать два операционных усилителя, можно выполнить гиратор и на одном (рис. 3.34, г). Для этой схемы (охваченной умеренной положительной обратной связью, поскольку операционный усилитель используется в режиме повторителя с коэффициентом передачи /С = 1) эквивалентная индуктивность L_M" = R_lR_iC. При этом R =(100−200) R₂, а входное сопротивление операционного усилителя Д_вх должно значительно превышать сопротивление резистора Я: R"" > /?,. Эквивалентная добротность фильтра сравнительно невелика:

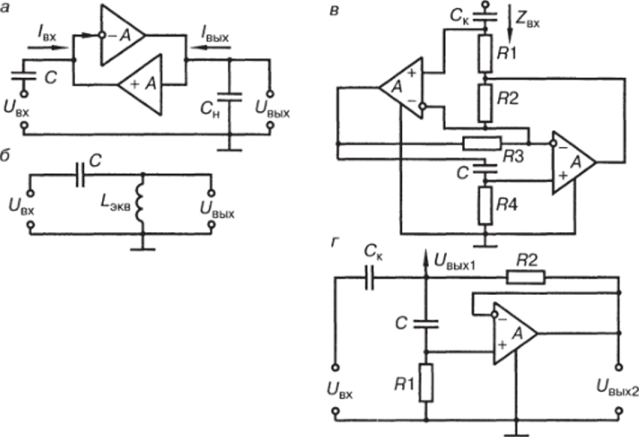
Рис. 3.34. Узкополосный активный фильтр на основе гиратора^;

его эквивалентная схема (б) усовершенствованная схема узкополосного гираторного фильтра (в): гираторный фильтр на основе одного операционного усилителя (г)

Рассмотренные полосовые активные фильтры на основе гиратора имеют достаточно стабильные параметры только при сравнительно небольших добротностях: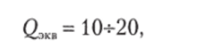

т. е. когда они являются достаточно широкополосными.

Соединяя фильтры последовательно, можно сузить полосу пропускания.

Так, например, для двух последовательно соединенных одинаковых узкополосных фильтров с добротностью Q каждый, эквивалентная добротность определяется как.

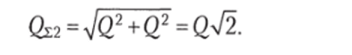
Для четырех фильтров.

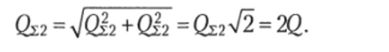
Таким образом, если необходимо уменьшить полосу пропускания в 2 раза (т. е. увеличить добротность в 2 раза), то необходимо включить последовательно четыре одинаковых фильтра, что не всегда возможно (и не всегда рационально).

Используя рассмотренный выше принцип построения компенсационных фильтров с обратной связью, можно создать очень стабильный узкополосный фильтр (&_кп> 10²) всего на трех-четырех операционных усилителях.

Подобные фильтры (называемые обычно «биквадратными») широко используются в современной электронной аппаратуре и выпускаются в виде стандартных интегральных микросхем.

Принципиальная схема одного из вариантов биквадратного узкополосного фильтра приведена на рис. 3.35, я, а на рис. 3.35, б — его эквивалентная схема. В последней схеме /С,(/со) — коэффициент передачи первого каскада, выполненного на операционном усилителе Л, и являющегося интегратором, т. е. фильтром нижних частот. Второй каскад — инвертирующий усилитель с коэффициентом передачи К₂. Третий каскад — фильтр нижних частот с коэффициентом передачи К₃(/со).

По аналогии со схемой усилителя, охваченного обратной связью, приведенной на рис. 2.4, можно записать для суммарного коэффициента передачи по выходу С/_вых2

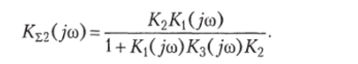
Коэффициенты передачи /С,(/со) и /С₃(/со) определяются как коэффициенты передачи операционных усилителей в инвертирующих схемах включения:

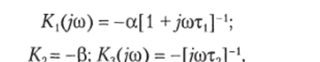
где, а = RJR_X р = Д₄/Я₃; т, = Д_КС,; т₂ = Д₅С₂.

Окончательно коэффициент передачи может быть выражен формулой.

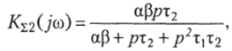
где р = jiо, т. е. имеет тот же самый вид, что и частотные характеристики полосовых усилителей с однои двухпетлевой отрицательными обратными связями. Если выходной сигнал снимать с третьего выхода ?/,_ых3, то коэффициент передачи оказывается как у двухполюсного фильтра нижних частот:

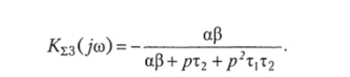
По первому выходу коэффициент передачи такой же, как у полосопропускающего фильтра:

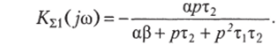
Расчет рассматриваемого биквадратного фильтра достаточно прост и сводится к следующему:

• 1) задаются требуемые величины: частота настройки/_р> коэффициент усиления на частоте резонанса К_ъ необходимое значение Q,_KH и емкости конденсаторов С, = С₂ = С;
• 2) вычисляется коэффициент k₀ = Q^_KJK_Z и определяются сопротивления Я, и R_K резисторов R и R_K: /?, = k₀/2nf_pC; R_K = Q^_KJ2nf_pC
• 3) сопротивления остальных резисторов должны быть подобраны в соответствие:

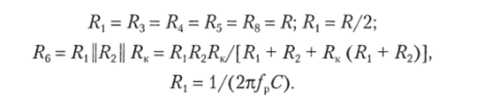
Полосовые фильтры с очень узкой полосой пропускания во многих случаях являются, в сущности, устройствами выделения синусоидального сигнала U_c(t) = U_c sin (o)_cr + ф_с), имеющего в спектре единственную, заранее известную частоту (0_С. И целью фильтрации в конечном.

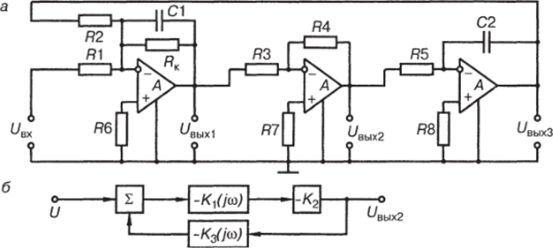
Рис. 3.35. Принципиальная схема биквадратного узкополосного фильтра^ и его эквивалентная электрическая схема (б).

итоге является выделение этого (и по возможности — только этого!) сигнала и измерения его амплитуды U_c и фазы <�р_с. В таких случаях возможности узкополосной фильтрации существенно расширяются, поскольку оказывается возможным использовать принципиально иные фильтрующие устройства, чем рассмотренные выше.

К числу таких устройств, широко используемых в качестве узкополосных фильтров, относятся синхронные детекторы и коммутируемые фильтры.

На рис. 3.36, а приведена функциональная схема синхронного детектора.

В этой схеме входной сигнал U_c (t) = U_c sin о + At/_n (t), содержащий гармоническую составляющую ?/_csinc? (которую надо выделить) и составляющую помех AU_n(t) (которую надо подавить), перемножается на опорный сигнал U_m (t) = U₀ sin о)_ct, содержащий «чистую», без всяких помех гармоническую составляющую той же частоты, что и сигнал (и когерентную ему). Напряжение с выхода перемножителя подается на интегратор:

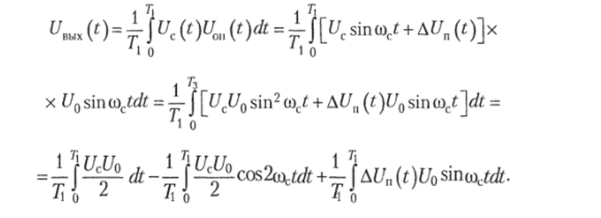
Вполне очевидно, что только первый интеграл в последнем выражении отображает постоянную составляющую и в результате интегрирования имеет значение, отличное от нуля: U_HUX(t) = Q, 5U_CU₀.

Таким образом, на выходе интегратора имеется результат от воздействия только полезного сигнала, а все составляющие напряжения помех, имеющих произвольные частоты, отфильтровываются. При этом степень подавления помех определяется временем интегрирования Г: чем оно больше, тем лучше подавление.

Количественно полоса пропускания синхронного детектора с временем интегрирования Г, может быть оценена так. Узкополосный фильтр с эквивалентной добротностью имеет время установления колебаний на своем выходе, определяемое из приведенных выше соотношений: Д/ДГ_уст * 1, но А/=fjQa_KB.

Поэтому Дг_усг = 1/Д/= Q,_K,/f_c = &_KJc-

Например, если имеется синхронный детектор, работающий на частоте /_с = 1 кГц; Г_с = 10 ³ с, с временем интегрирования Дt_yn = Т, = 1 с, то его эквивалентная добротность (3,_к, = Дг_уст/Г_с = 1/10″ ³ = 10³.

И это не предел, ибо время интегрирования может быть сколь угодно большим — вплоть до нескольких десятков-сотен часов (правда, столько же времени придется и ждать результатов, пока установится напряжение на выходе).

Следует отметить, что реализация синхронного детектора не всегда проста: ведь надо иметь опорный сигнал, когерентный (т. е. полученный от того же самого источника) измеряемому. В принципе, опорный сигнал можно генерировать и в самом измерительном устройстве, но он должен синхронизироваться (например, радиоприемом сигналов всемирного «точного времени») и иметь очень высокую стабильность частоты. Помимо этого следует учитывать тот факт, что в реальных условиях фаза ф_с измеряемого сигнала U, sin (ы_сг + (р_с) неизвестна и отличается от фазы опорного сигнала, вследствие чего сигнал на выходе синхронного детектора оказывается зависящим от ее значения: = O, 5l7_cf/₀cos (p.

Для устранения влияния фазы необходимо ее скомпенсировать, включив в цепь опорного сигнала регулируемый фазовращатель (что не всегда возможно, особенно при больших временах интегрирования) или усложнить схему синхронного детектора, введя в нее дополнительные элементы (рис. 3.36, б): фазовращатель на (р = п/2 для получения опорного напряжения U"cosm_ct, дополнительный второй перемножитель и интегратор, схемы возведения в квадрат и извлечения квадратного корня. При этом алгоритм работы такого синхронного детектора оказывается следующим:

где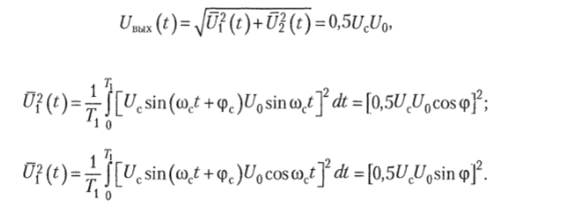

Несколько по иному принципу работают коммутируемые фильтры (рис. 3.37, а, б), которые также требуют для своей работы опорный сиг;

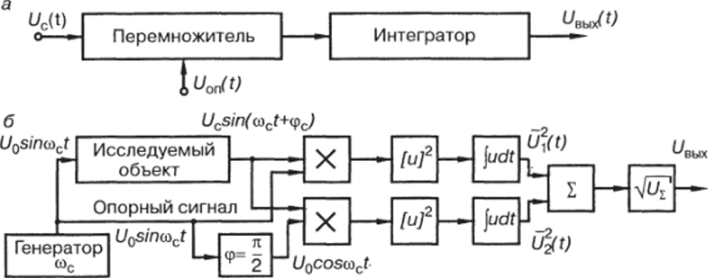
Рис. 3.36. Синхронный детектор, выполненный на основе перемножителя и интегратора (а); синхронный детектор, используемый в системе измерения частотных параметров исследуемого объекта (б)

нал, когерентный входному, но отличающийся от него по частоте в строго кратное число п раз. С этой частотой переключаются накопительные конденсаторы С1…Сп с помощью мультиплексора, работающего в циклическом режиме, вследствие чего период Т_с исходного сигнала U₀ (t) оказывается как бы разделенным на п участков (рис. 3.37, б) и каждый.

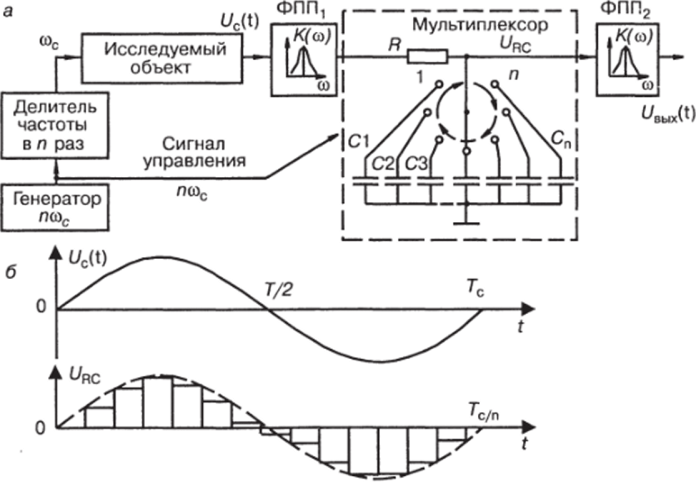
Рис. 3.37. Функциональная схема коммутируемого узкополосного фильтра (а) и диаграммы напряжений в различных точках его схемы (б)

участок сигнала U_RC интегрируется (усредняется) своим (и только своим) RC_X…RC" интегратором. Чем на большее число участков Т_с/п разделен фильтруемый сигнал и чем больше постоянная времени интегрирования RC_x…RC_n} тем выше эквивалентная добротность коммутируемого фильтра, определяемая как Q_)K" = 0,5na)_rRC.

В реальных подобных фильтрах получается Q_1KB < 10³. Помимо этого на входе и выходе обычно устанавливаются (рис. 3.37, а) дополнительные фильтры ФГ1П_] и ФПП₂ с умеренной добротностью (или ФНЧ и ФВЧ).

Контрольные вопросы.

• 1. Есть ли принципиальное отличие в амплитудно-частотных характеристиках нолосопропускающих фильтров, выполненных, но схемам рис. 3.33, д и рис. 3.33, е? Какой фильтр вы предпочли бы собрать для собственных исследований и почему?
• 2. Обьясните физику процессов в гираторе, используемом в качестве преобразователя емкостного импеданса в индуктивный.
• 3. Как бы вы изменили схему биквадратного фильтра, чтобы получить на его основе фильтр верхних частот (рис. 3.35, а)?