Проверка гипотезы о равенстве двух математических ожиданий

Сравнение двух математических ожиданий из нормально распределенных генеральных совокупностей X и Y, когда дисперсии а² И и а² [У] неизвестны, но есть основание считать, что они равны, сводится к проверке гипотезы.

Для проверки этой гипотезы используется критерий.

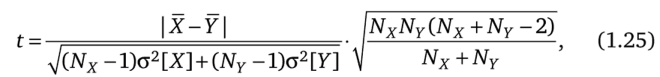
подчиняющийся закону распределения Стьюдента с числом степеней свободы m = (N_x + N_Y- 2). По таблице распределения Стьюдента следует найти значение ?_{а т}, соответствующее заданному уровню значимости, а и числу степеней свободы т.

Если вычисленное по формуле (1.25) значение t удовлетворяет неравенству t > t_a, то гипотезу Н₀ отвергают. Следует заметить, что условие нормальности, как и условие точного равенства дисперсий, не являются очень критичными.

Пример 1.2

Две бригады рабочих (10 и 15 человек) занимаются сборкой некоторых изделий, используя разные технологии сборки. Пусть X и Y — число собранных изделий рабочими одной и другой бригад соответственно. Эти величины можно считать нормально распределенными в силу центральной предельной теоремы. Кроме того, нет оснований считать дисперсии о²[Х] и о²[У] различными, т.к. рабочие в бригадах не подбирались специально по какому-либо признаку. Таким образом, предпосылки для применения t-критерия выполнены. Пусть в среднем, рабочий первой бригады собирает Х = 115 изделий, а второй бригады У = 100 изделий. Пусть также оценки дисперсий, вычисленные по формуле (1.17), равны а²Н = 205, а²[У] = 90. Тогда, согласно (1.25),.

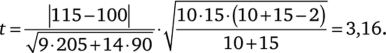
При уровне значимости, а = 0,05 и числе степеней свободы т — 23 критическое значение, определяемое по таблице распределения Стьюдента, t_0j05;23 ⁼ 2,068. Таким образом, t > t_{a m}. Гипотеза Н₀ отвергается. С вероятностью ошибки 0,05 можно утверждать, что одна технология лучше другой. Отличие X и У друг от друга не связано со случайным разбросом средних, а вызвано действительным отличием математических ожиданий двух генеральных совокупностей.

Проверка равенства дисперсий

Проверка гипотез, связанных с дисперсией, имеет большое значение, поскольку дисперсия характеризует такие величины, как ошибки измерительных приборов, воспроизводимость технологических процессов, точность стрельбы и т. п.

Нередко экспериментатора интересует, можно ли считать, что оценки дисперсий, вычисленные по данным нескольких выборок, являются оценками дисперсии одной и той же генеральной совокупности.

Если имеются две оценки дисперсий, то используют критерий Фишера (F-критерий).

Нулевая гипотеза Н₀: о²[Х] = а²[У].

Альтернативная гипотеза Н_г: а²[Х] ^ о² [У].

Критерий Фишера: F =.

a² [У].

Функция F подчиняется распределению Фишера (1.6). Предполагается, что о²[Х]><�з²[У] (X и У выбираются соответствующим образом). Задавшись уровнем значимости а, по таблице распределения Фишера находят критическое значение F_{a> т} где т₁ и т₂ — числа степеней свободы (т₁ = N_x- 1, т₂ = N_Y- 1). Если F < F_Kp, то принимается нулевая гипотеза о том, что 6²[Х] и с² [У] являются оценками дисперсии одной и той же генеральной совокупности. Если F > F_Kp, то принимается альтернативная гипотеза: выборки X и У относятся к разным генеральным совокупностям.

Если имеется больше двух выборок, то проверку равенства дисперсий производят по критерию Кохрена (если объемы всех выборок одинаковы) или по критерию Бартлетта (если они неодинаковы). Рассмотрим первый случай.

Н_г: Существует хотя бы одна из дисперсий, не равная другим дисперсиям.

Критерий Кохрена:

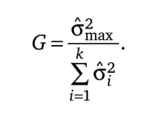
Критерий G имеет распределение Кохрена, из таблиц которого можно найти критическое значение G_{a к> т}, где, а — уровень значимости; к — число выборок; т — число степеней свободы, т = N, где N — объем выборок.

Пример 1.3

Двумя измерительными приборами X и Y произведены соответственно по 10 и 25 измерений одной и той же величины. Получены следующие оценки дисперсий: а²[Х] = 12,5; а² [7] = 7,0. Можно ли считать, что погрешности обоих приборов одинаковы?

Решение

Итак,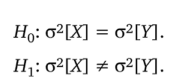

_т, «» о²[Х] 12,5, ^.

Критерии F = —-=-= 1,78.

^{Н Н} «ИЛ 7,0.

Критическое значение F_{a> т} при, а — 0,05 и т₁ = 10 — 1 = 9, т₂ = 25 — - 1 = 24 равно F_{0 05; 9}.₂₄ = 2,30. Поскольку F < F_a mi>m2, нулевая гипотеза принимается. Нет оснований считать, что погрешности приборов неодинаковы.

Пример 1.4

Измерялись значения емкости конденсаторов в пяти партиях. Брали по 15 штук из каждой партии. Требовалось проверить гипотезу о равенстве дисперсий.

Решение

Пусть по данным каждой из пяти выборок получены соответствующие статистические оценки дисперсий: а²[Х_х] = 50, d²[X₂] = 72, а²[Х₃] = 64,6²[Х₄] = 57, 6²[Х₅] = 60 (размерность не существенна для наших целей).

Итак: к = 5, т = N-1 = 15 — 1 = 14.

Критерий Кохрена.

Критическое значение G_{a k}, соответствующее а = 0,05, к = 5, т = 14, приводится в таблице: G_{0 05 5}.₁₄ = 0,38, т. е. G < G_{a к т}. Гипотеза о равенстве дисперсий не отвергается. Все партии конденсаторов в отношении разброса их значений можно считать не отличающимися друг от друга.