Другие работы

Концептуально близок к химерапластике и второй ГТ подход, направленный на коррекцию последовательности самого гена. Для многих генов показано, что отсутствие целого экзона функционально менее катастрофично для функции белка, чем сайтовые мутации, приводящие к сдвигу рамки считывания либо резко нарушающие конформацию белкового продукта, например, нонсенс мутации (возникновение стоп-кодона) при…
Реферат 
Парезы и параличи развиваются иногда уже на 3-й и 4-й день, иногда лишь спустя 1—1,5 недели. Необходимо помнить, что развитие их совсем не обязательно и может пройти едва заметно, так что все заболевание может походить на легкий грипп или простудное заболевание. Параличи развиваются с различной быстротой. При поражениях спинного мозга чаще всего наблюдаются параличи мышц бедер, голеней, туловища…
Реферат 
При физикальном обследовании у большинства больных определяется умеренное увеличение границ сердца. При аускультации над областью сердца слышен систолический шум, максимальное звучание которого обнаруживается у грудины в III межреберье слева и выше во II межреберье. Шум хорошо проводится на аорту и крупные сосуды и бывает различной интенсивности. Чаще он продолжительный, занимает всю систолу…
Реферат 
Болевая импульсация от тела организма поступает по Aди С-волокнам — это дендриты биполярных нейронов спинальных ганглиев (первые нейроны), они вступают в спинной мозг, как и все чувствительные волокна, в составе задних корешков. Аксоны этих нейронов в спинном мозге переключаются, в основном, в задних рогах (вторые нейроны). С-волокна направляются в ствол мозга в составе латерального…
Реферат 
Неблагоприятные последствия избыточного питания на фоне малой физической нагрузки позволяют считать, что одним из основных принципов рационального питания при интеллектуальном труде должно быть снижение энергетической ценности питания до уровня производимых энергетических затрат или повышение физической нагрузки до уровня калорийности потребляемой пищи Биологическая ценность пищи определяется…
Реферат 
Для получения оценки работы отдельного врача уровни качества (УК) по проверенным амбулаторным картам суммируются и делятся на число проанализированных карт. Д 1- объема (от количества зарегистрированных заболеваний) и выявления больных при профосмотрах; Д 2- своевременности взятия на учет (на протяжении 3-х месяцев после выявления); Возможная схема экспертной оценки качества медицинской помощи…
Реферат 
В настоящее время для достоверной, быстрой и четкой диагностики причины бесплодия имеются все условия: современные высокоинформативные диагностические методы и значительный практический опыт по этой проблеме. Необходимо обоснованно и аргументированно использовать имеющиеся возможности, быстро и объективно оценить состояние репродуктивной системы, определить причину бесплодия и помнить, что…
Реферат 
В крови людей, страдающих гемофилией, нет компонента фибриногена, необходимого для её быстрого свёртывания. У таких людей происходит потеря большого количества крови даже при легких ранениях и незначительных операциях. Рассматривая историю рода, в котором есть ген, вызывающий гемофилию, учёные установили, что это заболевание передаётся потомству здоровыми женщинами, но не передаётся мужчинами…
Реферат 
Больным считает себя две недели назад, когда впервые стала отмечать ноющие боли в области поясницы. К врачу не обратилась, препараты не принимала. На следующее утро у больной появились озноб, сильный жар, повышение температуры до 390С, затем в течение дня тошнота и рвота. В течение 5 дней лечилась сама, принимала Парацетамол.04.19 вызвала бригаду скорой помощи и была доставлена в урологическое…
Реферат 
Необходимые действия и научные исследования, направленные на улучшение здоровья России Здоровьенаселения в интерпретации Всемирной организации здравоохранения (ВОЗ) определяется как состояние полного физического, духовного и социального благополучия, а не просто отсутствие болезни или немощи. Оно определяет возможности развития и поддержания образования, профессиональной подготовки…
Реферат 
Хорошая электрощетка предусматривает несколько скоростей работы. Современные щетки имеют три скорости, однако стоматологам доказано, что обычному потребителю достаточно двух скоростей. Современные электрические зубные щетки производят в основном вибрационные и ротационные движения, что позволяет повысить их очищающие способности. Автоматические движения данной щетки освобождают пациента…
Реферат 
Открытия экзон-интронной организации эукариотических генов и возможности альтернативного сплайсинга показали, что одна и та же нуклеотидная последовательность первичного транскрипта может обеспечить синтез нескольких полипептидных цепей с разными функциями или их модифицированных аналогов. Например, в митохондриях дрожжей имеется ген box (или cob), кодирующий дыхательный фермент цитохром Ь…
Реферат 
Парапневмонические, постпневмонические. В качестве этиологии — любые кокки. Предрасполагает хронический алкоголизм — в 5 — 6 раз чаще, ослабление иммунитета. Метапневмонические проявляются через 7 — 10 дней рецидивом лихорадки. Эмпиема плевры связана с деструкцией. Абсцесс секвестрирует в плевральную полость. Симптомы тяжелой гнойной интоксикации: гектическая температура, ознобы, ночные выпоты…
Реферат 
Персонал, занятый в производстве медицинских газов, должен понимать требования настоящего стандарта в отношении медицинских газов, знать критически важные аспекты и возможную опасность для пациентов, которую могут представлять лекарственные препараты в форме медицинских газов. Помещения, в которых выполняются операции по производству, проведению испытаний и хранению медицинских газов, должны…
Реферат 
Патологические элементы кожных покровов. При обнаружении патологических элементов необходимо указать их особенности, локализацию и распределение на теле, характер расположения, конкретный вид и время их возникновения (например, при сыпи). Следствием зуда кожи могут быть расчесы, которые приводят к риску инфицирования пациента. При осмотре необходимо обратить на них особое внимание, так как…
Реферат 
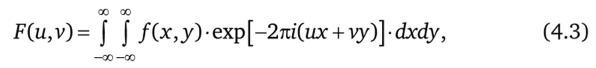
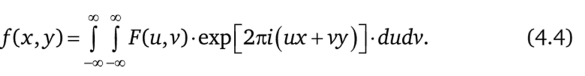
![Поперечное изображение мозга и его соответствующее двумерное преобразование Фурье [4].](/img/s/8/83/1643683_3.png)