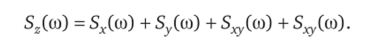Стационарные случайные процессы

Весьма важным классом случайных процессов, позволяющим получить точное или приближенное статистическое описание сигналов в САУ, являются стационарные случайные процессы.

Случайный процесс называется стационарным, если статистические характеристики его не зависят от текущего времени. К стационарным процессам относятся, например, шумы в радиоэлектронной аппаратуре, колебания искусственных спутников Земли относительно своего центра массы, качка корабля, тепловые шумы и т. д. Математический аппарат для исследования стационарных процессов более разработан.

Многие нестационарные процессы удается описать с помощью стационарных, сохраняя приемлемую точность исследования. На практике исследуются реализации на конечном интервале времени, в течение которого случайный процесс можно считать стационарным. Это, например, можно делать, когда за время длительности процесса в САУ статистические характеристики сигналов не успевают существенно измениться.

Различают стационарность в узком и широком смысле.

Случайный процесс x (t) называется стационарным в узком смысле, если его n-мерная плотность вероятности р_п(.х_ь …, х_п; t_b …, t") при любом значении п не изменяется с изменением начала отсчета времени на величину At:

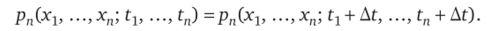
Случайный процесс x (t) называется стационарным в широком смысле, если математическое ожидание его не зависит от времени, а корреляционная функция — функция разности т = t_x — t₂, т. е.

Случайный процесс, стационарный в широком смысле, в некоторых случаях может быть нестационарным в узком. Однако случайный процесс, стационарный в узком смысле, обязательно является стационарным в широком смысле.

При дальнейшем изложении будем рассматривать стационарные процессы в широком смысле.

Если имеется два случайных процесса х (0 и y (t) то для их описания по аналогии с предыдущим вводится понятие стационарной связанности в узком и широком смыслах.

Стационарно связанными в узком смысле называются случайные процессы x (t) и y (t), если их совместная п-мерная плотность вероятности р_п(х_г, …, х_п; t_a, …, t_n) = p_n(x_lt х_п; у_т+ь …, у_п, t_a, …, t") при любых пит зависит только от величины интервалов t₂ — t_v …, t_n — t₁ и не зависит от положения этих интервалов на оси времени t.

Стационарные случайные процессы x (t) и y (t) называются связанными в широком смысле, если их взаимная корреляционная функция R_xy(t₁, t₂) зависит только от разности т = t_x -1₂ и не равна нулю.

Для стационарных и стационарно связанных случайных центрированных процессов x (t) и y (t) взаимная корреляционная функция.

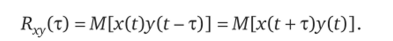
Если для стационарного процесса статистические характеристики, полученные усреднением по множеству реализаций при фиксированном времени, совпадают с характеристиками, полученными усреднением по времени одной реализации в достаточно большом интервале наблюдения, то такие стационарные процессы называются эргодическими.

Для эргодического процесса его отдельная реализация на бесконечном отрезке времени полностью определяет весь случайный процесс с его бесконечными реализациями. Чтобы вычислить статистические характеристики этого процесса, можно ограничиться одним опытом, проводимым в течение достаточно большого интервала времени, вместо множества реализаций, необходимых для нахождения характеристик неэргодического процесса.

Для эргодического процесса справедливы следующие соотношения, характеризующие его основные статистические характеристики.

Математическое ожидание и среднее значение.

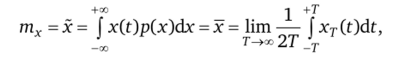
где первый интеграл, обозначенный как х, означает усреднение по множеству реализаций; второй интеграл, обозначенный как х, — усреднение по времени одной реализации при Т —> оо; xr (t) — реализации стационарного случайного процесса, рассматриваемого на интервале времениT.

Приведенное выражение означает, что для эргодического процесса среднее по множеству реализаций равно среднему по времени для одной реализации. Чем больше интервал усреднения по времени, тем точнее определяется математическое ожидание.

Дисперсия.

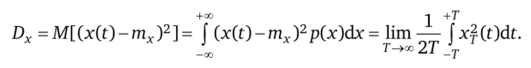
Корреляционная функция.

Как очевидно из последнего соотношения при, т = 0 корреляционная функция равна дисперсии случайного процесса:

Взаимная корреляционная функция двух случайных взаимно зависимых случайных процессов x (t) и y (t) определяется согласно выражению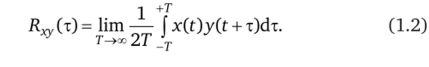

Взаимная корреляционная функция характеризует статистическую зависимость между значениями двух случайных процессов x (t) и у (0 в два совпадающих или различных момента времени.

При исследовании САУ часто используют нормированные корреляционные и взаимные корреляционные функции. Если случайные процессы x (t) и y (t) стационарны и стационарно связаны, то нормированные корреляционная г_х(т) и взаимная корреляционная г^(т) функции определяются соотношениями.

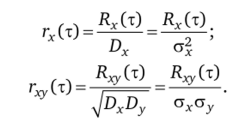
Рассмотрим некоторые свойства корреляционных функций.

1. Корреляционная функция R_x(т) стационарного случайного процесса есть четная функция:

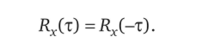
Поэтому при графическом представлении корреляционная функция всегда симметрична относительно оси ординат. Корреляционная функция стационарного случайного процесса симметрична относительно переменных t_b f₂, т. е.

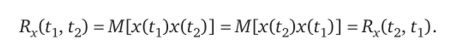
2. Значение корреляционной функции в нуле всегда превышает ее значение в любой другой момент времени т:

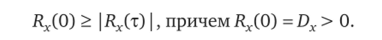
3. Корреляционная функция при т —" °о определяется соотношением.

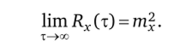
Это говорит о том, что в бесконечно удаленные друг от друга моменты времени значения случайного процесса являются независимыми и корреляционная функция будет не равна нулю только за счет присутствия детерминированной постоянной составляющей в виде математического ожидания т_х. Для центрированного случайного процесса й_х(°°) = 0.

4. Чем быстрее убывает корреляционная функция ЯДт), тем более высокие частоты будут содержаться в случайном процессе x (t). Следовательно, корреляционная функция может характеризовать инерционные свойства объекта: чем быстрее затухает кривая Д.(т), описывающая сигнал на выходе объекта, тем объект менее инерционен.

В большинстве задач, встречающихся в практике построения САУ, корреляционные функции сигналов имеют вид монотонно убывающих функций.

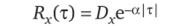
либо затухающих осциллирующих функций, например, типа.

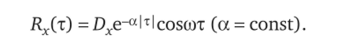
Корреляционные функции указанного типа представлены, соответственно, на рис. 1.4, а и б. При этом степень коррелированное™ случайного процесса можно характеризовать так называемым интервалом или временем корреляции.

Рис. 1.4. Вид типовых корреляционных функций.

5. Время корреляции т_к случайного процесса x (t) представляет интервал времени между двумя сечениями x (t) и x (t + т), начиная с которого можно практически считать некоррелированными случайные величины x (t) и x (t + т). Время корреляции т_к может быть найдено из условия.

где Д = (0,01 ч- 0,05)Я_А(0).

За пределами этого отрезка времени корреляционная функция определяется величиной Д. Если R_x(x) = D_xe~^axI, то т_к ~ 3/а.

6. Корреляционная функция стационарного случайного процесса z (t) = x (t) +y (t), где x (f) и j (t) — стационарные случайные процессы:

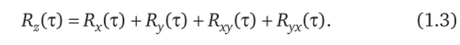
Спектральная плотность случайного процесса. При статистическом исследовании САУ для стационарных процессов удобно пользоваться понятием спектральной плотности. Спектральная плотность — важная характеристика случайных процессов. Знание ее позволяет оценивать качество работы САУ. Обозначается она S_A(co) и определяется как преобразование Фурье от корреляционной функции:

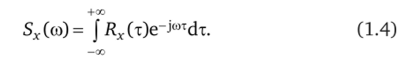
Учитывая, что ег)^м = cosoot — jsincox, a R_x(т) — вещественная четная функция, получим.

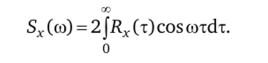
Если известна спектральная плотность случайного процесса, то, пользуясь обратным преобразованием Фурье, можно определить корреляционную функцию:

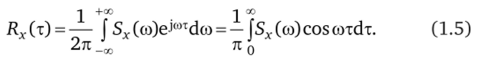
Последние соотношения называются формулами Винера — Хинчина. При т = 0 на основании выражения (1.5) можно определить среднее значение квадрата случайной величины:

Для уяснения физического смысла спектральной плотности S_A((о) рассмотрим реализацию стационарного случайного процесса x (t) в виде электрического тока, протекающего через сопротивление в 1 Ом. Средняя мощность, выделенная за время 2 Г на этом сопротивлении:

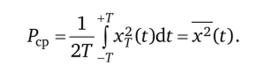
Если увеличить интервал наблюдения 2Т до бесконечных пределов интегрирования, то согласно формуле Парсеваля можно от интегрирования по времени перейти к интегрированию по спектру частот со:

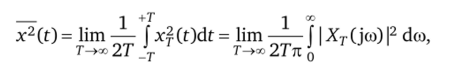
где X_r(jco) — текущий спектр процесса x_r(t).

Связь между x_T(t) и X_r(jw) осуществляется через преобразование Фурье:

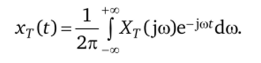
Тогда с учетом формулы (1.5а) спектральная плотность случайного процесса запишется в виде.

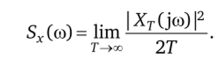
Средняя мощность Р_ср с учетом последнего выражения.

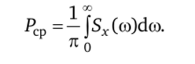
Это соотношение характеризует мощность во всем диапазоне частот. ^.

Каждая элементарная составляющая вида — S_A.(co)dco соответ;

к

ствует мощности в бесконечно узкой полосе частот doo, а коэффициент —(со) определяет скорость нарастания мощности к

по частоте, или плотность мощности в спектре. Таким образом, спектральная плотность S_x(co) характеризует распределение мощности составляющих в интервале частот doo.

По аналогии со взаимной корреляционной функцией вводится понятие взаимной спектральной плотности двух стационарных зависимых случайных процессов.

Для случайных процессов x (t) иу (0.

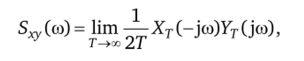
где ХД-jco) — функция, комплексно сопряженная с функцией адо.

Взаимная спектральная плотность (со) — комплексная величина и физического смысла не имеет. Она характеризует связь двух случайных процессов.

Если ЯдуСт) — взаимная корреляционная функция двух стационарно связанных случайных процессов x (t) иу (0, то взаимная спектральная плотность.

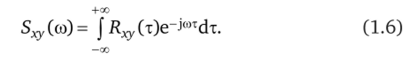
И наоборот, при известной взаимной спектральной плотности S^yCw) взаимная корреляционная функция может быть определена из следующего выражения:

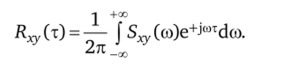
Рассмотрим свойства спектральной плотности.

1. Спектральная плотность S_x(co) стационарного случайного процесса является четной действительной функцией:

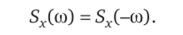
2. Спектральная плотность S_A.(oo) стационарной случайной функции есть функция неотрицательная.

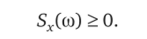
3. Дисперсия стационарного случайного процесса x (t).

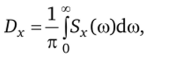
т. е. дисперсия пропорциональна площади, ограниченной кривой спектральной плотности и осью абсцисс.

• 4. Если R_x(t) — монотонная убывающая функция от т, то S_x(ft>) тоже монотонная убывающая функция.
• 5. Чем шире график корреляционной функции Я_х(х), тем уже график спектральной плотности S_x(ot)). Это соответствует физической сущности случайного процесса: чем медленнее протекает процесс и сильнее взаимосвязь между соседними точками, тем меньшее значение в процессе имеют высокие частоты.
• 6. Спектральная плотность случайного процесса z (t), являющегося суммой двух стационарных случайных процессов х (0 иу (0: