Оценка погрешности метода Монте-Карло

Пусть для получения оценки а математического ожидания а₀ случайной величины X было произведено п независимых испытаний (разыграно п возможных значений X). По результатам испытаний была найдена выборочная средняя х, которая принята в качестве искомой оценки: а = х.

Если повторить опыт, то будут получены другие возможные значения X, следовательно, другая средняя, а значит, и другая оценка а. Поэтому получить точную оценку математического ожидания невозможно. Таким образом, возникает вопрос о величине допускаемой ошибки при оценке параметра а.

Ограничимся вычислением лишь максимальной величины ошибки Д с заданной доверительной вероятностью у:

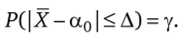
Максимальная величина ошибки Д есть не что иное, как «точность оценки» математического ожидания по выборочной средней с помощью доверительных интервалов (см. параграф 8.3).

Рассмотрим наиболее часто встречающихся в прикладных задачах три варианта задания случайной величины.

1. Случайная величина X распределена нормально и ее среднее квадратическое отклонение а известно. В этом случае с доверительной вероятностью у максимальная величина ошибки (см. параграф 8.3).

где п — число испытаний (разыгранных значений X); t — значение аргумента функции Лапласа, при котором Ф (0 = у.

С доверительной вероятностью у = 0,95 найти максимальную величину ошибки Д, если для оценки математического ожидания нормальной величины X с известным средним квадратическим отклонением, равным 0,5, было разыграно 100 возможных значений X.

Решение. По условию задачи п = 100, а = 0,5, Ф (?) = 0,95.

По таблице функции Лапласа (см. приложение 3) находим t = 1,96. Тогда максимальная величина ошибки: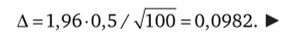

2. Случайная величина X распределена нормально, причем ее среднее квадратическое отклонение о неизвестно. В этом случае с доверительной вероятностью у максимальная величина ошибки (там же):

где t_y — коэффициент Стьюдента (приложение 5); s — исправленное среднее квадратическое отклонение.

Пример 10.6.

С доверительной вероятностью у = 0,95 найти максимальную величину ошибки Д, если для оценки математического ожидания нормальной величины X было разыграно 30 ее возможных значений и по ним найдено исправленное среднее квадратическое отклонение s = 0.5.

Решение. По условию п = 30, 5 = 0,5. Используя таблицу приложения 3, по у = 0,95, п = 30 находим [. = 2,04. Максимальная величина ошибки: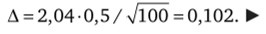

Заметим, что чем больше испытаний п, тем меньше различие между результатами, которые дают формулы (10.1) и (10.2). Это объясняется тем, что при п —"распределение Стьюдента стремится к нормальному (см. параграф 8.3).

3. Случайная величина X распределена по закону, отличному от нормального. В этом случае при достаточно большом числе испытаний (п > 30) с доверительной вероятностью у, максимальная величина ошибки может быть вычислена по формуле (10.1), если среднее квадратическое отклонение, а случайной величины X известно; если же а неизвестно, то можно подставить в эту формулу его оценку s — исправленное среднее квадратическое отклонение либо воспользоваться формулой (10.2).

Замечание

Если необходимо найти наименьшее число испытаний, которые обеспечат наперед заданную максимальную величину ошибки Д, надо выразить п из формул (10.1) или (10.2). Имеем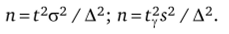

Сколько необходимо провести испытаний (розыгрышей), чтобы максимальная величина ошибки Д не превышала 0,098 с доверительной вероятностью у = 0,95.

Решение. По условию задачи Д = 0,098; о = 0,5; (t) = 0,95. По таблице функции Лапласа (см. приложение 3) находим t = 1,96. Тогда минимальное число испытаний, при которых ошибка не превысит 0,098, равно: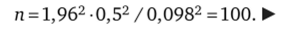

Вопросы и задания для самоконтроля

• 1. В чем суть имитационного статистического моделирования?
• 2. В чем заключается метод Монте-Карло?
• 3. Как производится розыгрыш случайной величины?
• 4. Каким образом разыгрываются события?
• 5. Каким образом производится оценка максимальной величины ошибки метода Монте-Карло?
• 6. Чем отличается коэффициент Стьюдента от аргумента функции Лапласа?

Задачи для самостоятельного решения

1. Разыграть пять значений дискретной случайной величины X, закон распределения которой задан в виде таблицы:

• 2. Разыграть семь испытаний, в каждом из которых вероятность появления события, А равна 0,7.
• 3. Заданы вероятности трех событий, образующих полную группу: Р (А,) = = 0,2; Р (А₂) = 0,3; Р (А₃) = 0,5. Разыграть семь испытаний, в каждом из которых появляется одно из заданных событий.
• 4. События, А и В независимы и совместны. Разыграть семь испытаний, в каждом из которых вероятность появления события, А равна 0,3, а события В — равна 0,8.