Подключение бесконечно протяженной линии без утечки к источнику постоянного напряжения

Полагаем G₀ = 0 и из формул (12.44) и (12.45), обозначив о = 1/ VZC; b = R₀/(2Lq), определим.

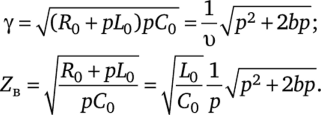
Изображение напряжения в начале линии L/₁(0, р) = U/p. В соответствии с формулами (11.37) и (11.38) изображение напряжения и тока в точке, удаленной на расстояние х от начала линии,.

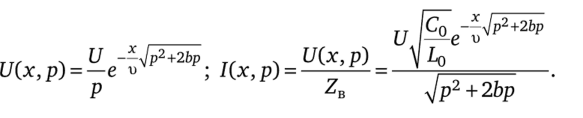
Для определения тока i (x, t) как функции времени t и расстояния х (для t > х/х> = т) воспользуемся табличным соотношением.

где J₀0'bVt²-T²) — бесселева функция нулевого порядка от мнимого аргумента. Значения ее приведены в табл. 15.1. Следовательно,.

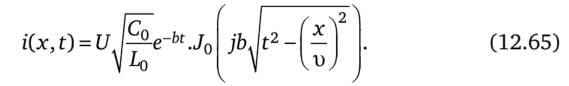
В соответствии с (12.65) на рис. 12.10, б изображена зависимость.

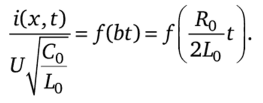
Из рисунка ясно, что при малых х (малых RqX/(2v>L₀)) ток i, получив большой начальный толчок, уменьшается во времени. При больших значениях х ток i после скачка сначала возрастает, а затем уменьшается. Так как для линии с распределенными параметрами, у которой Эи 1 di

^G° ^{= 0}'dt⁼~C^dx'

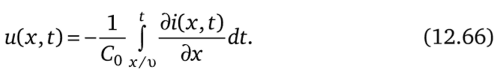
Возьмем частную производную от i (x, t) (см. (12.65)) по х, подставим ее в (12.66) и учтем также напряжение, обусловленное скачком тока на фронте волны. В результате получим.

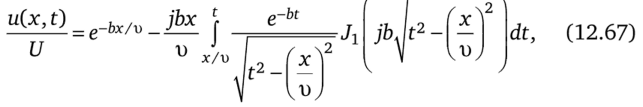
где J₁ — функция Бесселя первого порядка от мнимого аргумента (см. табл. 15.1). Слагаемое е~^Ъх/ь в (12.67) соответствует скачку тока на фронте волны. На фронте волны в точке х в момент х/х> ток равен.

[с~

U — e~^bx/v, а в соседней точке х + Ах в тот же момент времени ток еще V Lo

отсутствует. Поэтому напряжение, вызванное скачком тока на фронте волны,.

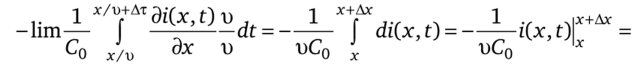
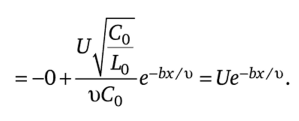
Вопросы для самопроверки

• 1. При каких допущениях на первом этапе изучения рассматривают переходные процессы в линиях с распределенными параметрами? Какими дифференциальными уравнениями описывают эти процессы?
• 2. Как понимать, что аргументами функций, являющихся решением, оказываются (t — х/о) и (t + х/о)?
• 3. Как показать, что для линии без потерь характер изменения и или i падающей волны в любой точке линии повторяет характер изменения и и I в начале линии, но с запозданием во времени?
• 4. Как согласовывают переходные процессы в линиях с распределенными параметрами с переходными процессами в нагрузке на конце линии?
• 5. Обоснуйте методику составления схем замещения для исследования волновых процессов, когда волна дойдет до нагрузки.
• 6. Как из временных графиков напряжения и_н на нагрузке и тока i_H в нагрузке получить графики отраженных волн и₀ и i₀ на линии?
• 7. Какова идея расчета переходных процессов в линии с распределенными параметрами при отключении нагрузки или части ее?
• 8. Охарактеризуйте стадии волнового процесса при подключении разомкнутой на конце линии длиной I к источнику постоянного напряжения, полагая сначала для линии R₀ = G₀ = 0, а затем что линия является линией без искажения.
• 9. Как от уравнений для мгновенных значений тока и напряжения перейти к уравнениям, записанным для операторных изображений этих величин?
• 10. В каком случае в качестве линии задержек используют линию с распределенными параметрами, а в каком — каскадное соединение фильтров НЧ?
• 11. Объясните идею формирования кратковременных импульсов с помощью линии с распределенными параметрами.
• 12. Решите задачи 15.5; 15.6; 15.12; 15.17.