Основные соотношения для трансформатора со стальным сердечником

В параграфе 3.39 рассматривались соотношения, характеризующие работу трансформатора, для которого зависимость между напряженностью поля и потоком в сердечнике была линейной, а потери в сердечнике отсутствовали.

Для улучшения магнитной связи между первичной (м/Д и вторичной (w₂) обмотками трансформатора его сердечник выполняют из ферромагнитного материала (рис. 15.51, в)¹.

В данном параграфе рассмотрены соотношения, характеризующие работу трансформатора с учетом того, что зависимость между напряженностью поля и потоком в ферромагнитном (стальном) сердечнике нелинейна и что в сердечнике есть потери, обусловленные гистерезисом и вихревыми токами.

Для уменьшения тока холостого хода сердечник трансформатора стремятся изготовить таким образом, чтобы он имел возможно меньший воздушный зазор, расположенный перпендикулярно магнитному потоку, либо совсем не имел его.

В силу нелинейной зависимости между потоком и напряженностью поля в сердечнике по обмоткам трансформатора протекают несинусоидальные токи^[1][2].

Анализ работы трансформатора будем проводить, заменив несинусоидальные токи и потоки их эквивалентными в смысле действующего значения величинами: Д — комплекс действующего значения тока первичной обмотки; 1₂ — комплекс действующего значения тока вторичной обмотки; Ф_ь — комплексная амплитуда основного магнитного потока, проходящего по сердечнику трансформатора, пронизывающего обмотки w₁ и w₂ и наводящего в них ЭДС.

Вследствие наличия рассеяния небольшой по сравнению с Ф_т поток — поток рассеяния первичной обмотки Ф₁₅ — замыкается по воздуху, образуя потокосцепление только с обмоткой w_v Другой, также небольшой по сравнению с Ф_т поток — поток рассеяния вторичной обмотки Ф₂₅ — замыкается по воздуху, сцепляясь только с обмоткой w₂.

Полагают, что потокосцепление потока Ф₁₅ с обмоткой w₁ пропорционально току ip

Коэффициент пропорциональности L_ls между потокосцеплением j/_ls и током Д называют индуктивностью рассеяния первичной обмотки; L_ls зависит от числа витков и конструкции обмотки.

Принимают также, что потокосцепление j/₂₅ потока Ф_2х с обмоткой w₂ пропорционально току вторичной цепи /₂:

Коэффициент пропорциональности L_2s между потокосцеплением j/_2s, обусловленным потоком рассеяния Ф₂₅, и током /₂ называют индуктивностью рассеяния вторичной обмотки; L_2s зависит от числа витков и конструкции вторичной обмотки.

Индуктивное сопротивление первичной обмотки, обусловленное потоком рассеяния Ф₁₅,.

Аналогично индуктивное сопротивление вторичной обмотки, обусловленное потоком рассеяния Ф_2х,.

Пусть — резистивное сопротивление первичной обмотки; R₂ — резистивное сопротивление вторичной обмотки; Z_H — сопротивление нагрузки.

На рис. 15.52, а изображена схема того же трансформатора, что и на рис. 15.51, в, но на ней резистивные и индуктивные сопротивления, обусловленные потоками рассеяния, представлены отдельно выделенными R_lf X_ls, R₂, Х^. Запишем уравнение по второму закону Кирхгофа для обеих цепей.

Рис. 15.52.

Для первичной цепи

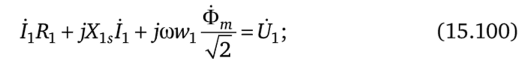
для вторичной цепи.

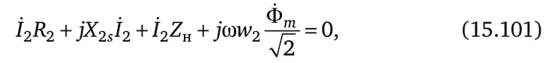
где j (tiw₁ — напряжение, численно равное ЭДС, наводимой в обv 2.

мотке w₁ основным рабочим потоком Ф_т. Деление Ф_т на V2 объясняется переходом от амплитудного значения к действующему. Аналогично Ф.

;cow₂ —т=- — напряжение, численно равное ЭДС, наводимой в обмотке w₂ v2.

основным рабочим потоком Ф_т.

Обозначим ток при холостом ходе трансформатора через /₀. МДС трансформатора при холостом ходе равна МДС трансформатора при наличии тока /₂ составляет i₁w₁ + l₂w₂. Трансформаторы конструируют обычно таким образом, чтобы падения напряжения и jiiX_ls

Ф были много меньше, чем падение напряжения jcowj—Если это.

v 2.

учесть, то для правильно сконструированных трансформаторов уравнение (15.100) запишем так:

Уравнение (15.102) справедливо как при холостом ходе, так и при нагрузке, т. е. при переходе от холостого хода к режиму работы при нагрузке поток Ф_т практически остается неизменным по модулю.

Но если в этих двух режимах поток Ф_т один и тот же, то должны быть равны и создающие его МДС, т. е.

Поделив обе части равенства на w_1} получим

где.

Таким образом, ток первичной цепи может быть представлен как геометрическая сумма двух токов: тока холостого хода 1₀ и тока /₂. Ток Г₂ называют приведенным (к числу витков первичной обмотки) вторичным током. Он численно равен току /₂, измененному в w₂/w₁ раз. Кроме того, в правильно сконструированных трансформаторах паде;

".. Ф_т

ния напряжении I₂R₂ и j/₂X_2s малы по сравнению с jcow₂ —7=-, поэтому.

V2.

из уравнения (15.101) следует, что.

Если почленно разделить (15.102) на (15.106) и перейти к модулям, то.

т. е. отношение напряжения на входе трансформатора к напряжению на его выходе (на нагрузке) приблизительно равно отношению числа витков первичной обмотки к числу витков вторичной обмотки.

В правильно сконструированных трансформаторах при нагрузке, близкой к номинальной, ток 1₀ составляет 1—10% тока 1_Ь поэтому уравнение (15.103) можно приближенно представить так:

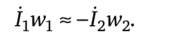
Между модулями токов 1_г и 1₂ при нагрузке, близкой к номинальной, имеет место следующее приближенное соотношение:

т. е. ток 1_г почти пропорционален току 1₂. Эта пропорциональность немного нарушается за счет тока холостого хода /₀.

В резистивных сопротивлениях вторичной цепи выделяется энергия, которая переносится магнитным потоком из первичной цепи во вторичную и восполняется источником питания схемы. На рис. 15.52, б изображена схема замещения трансформатора со стальным сердечником. Для ее обоснования уравнение (15.101) умножим на w_x/w₂, заме;

• W-]

ним в нем ток 1₂ на -1₂ —- в соответствии с (15.105) и у всех слагаемых.

w₂

уравнения изменим знаки. В результате получим.

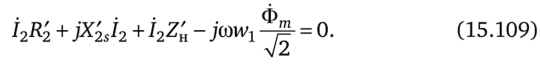
Приведенные сопротивления.

Схема на рис. 15.52, б удовлетворяет уравнениям (15.100), (15.103) и (15.109).

• [1] На рис. 15.51, в и 15.52 для большей наглядности обмотки w1 и w2 показаны находящимися на разных стержнях. Практически их располагают обычно на одном и том же стержне.
• [2] Несинусоидальность проявляется главным образом в режимах работы, близкихк холостому ходу.