Метод малого параметра

Нелинейные дифференциальные уравнения иногда решают путем последовательных приближений, представляя искомую величину х в виде ряда по степеням некоторого коэффициента ц, который называют малым параметром:

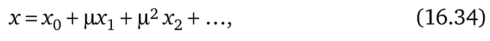
где х₀ — решение уравнения нулевого приближения (последнее получают из исходного, полагая, что все нелинейные члены в исходном уравнении отсутствуют); х₁ — решение уравнения первой поправки, которая учитывает влияние нелинейных членов в первом приближении; х₂ — решение уравнения второй поправки и т. д.

Если исходное уравнение является дифференциальным уравнением второго или более высокого порядка, а принужденный режим представляет собой колебательный процесс, то квадрат угловой частоты первой гармоники о² или первую степень со также разлагают в ряд по малому параметру:

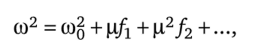
где cOq — квадрат угловой частоты в нулевом приближении, когда всеми нелинейными членами пренебрегают; х/_г — поправка первого приближения, вызванная нелинейными членами уравнения; ц²/₂ — поправка второго приближения и т. д.

Последовательность решения рассмотрим на двух примерах.

1. При х (0) = 0 решить уравнение.

К такому уравнению, например, сводится задача о переходном процессе в цепи, состоящей из нелинейной индуктивности с нелинейной ВАХ и линейного резистивного сопротивления, при подключении ее к источнику постоянного напряжения и при квадратичной аппроксимации зависимости потокосцепления от тока.

Линейные члены уравнения переносим в левую часть, а нелинейные, умножив на некоторый малый параметр ц, — в правую (в примере ц = 1):

Представим решение (16.35) в виде ряда по степеням р:

Подставим (16.37) в (16.36):

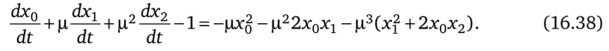
Из (16.38) образуем систему уравнений, приравняв члены левой и правой частей его при одинаковых степенях ц: уравнение нулевого приближения.

уравнение для первой поправки.

уравнение для второй поправки.

Проинтегрируем (16.39): х₀ = t + С₀.

Постоянную С₀ = 0 определили из начальных условий.

Подставим х₀ = t в уравнение (16.40) и проинтегрируем его:

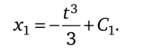
Для первой поправки начальные условия также нулевые, поэтому С_х = 0; t³

=——. Подставим значения х₀ и X] в (16.41):

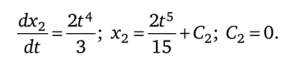
В соответствии с (16.37).

Аналогично можно было бы получить и последующие члены ряда (16.37). Так как уравнение (16.35) имеет точное решение х = tht, то, взяв в разложении tht три первых члена ряда, можно убедиться, что они совпадают с правой частью (16.42).

2. Решить уравнение для лампового генератора (вывод уравнения см. в примере 164) при начальных условиях х (0) = А₀, х'(0) = 0:

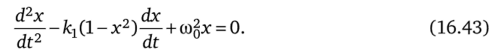
Коэффициент к_г при нелинейном члене в дальнейшем будем считать малым параметром и обозначим р. В соответствии с предыдущим.

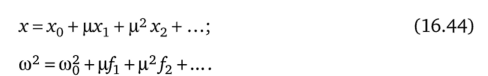
В уравнении (16.43) вместо х подставим правую часть (16.44) и со² — р/₂ — - р²/₂ вместо о)^:

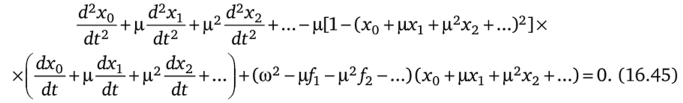
Образуем из (16.45) три уравнения, соответствующих р в нулевой, первой и второй степенях:

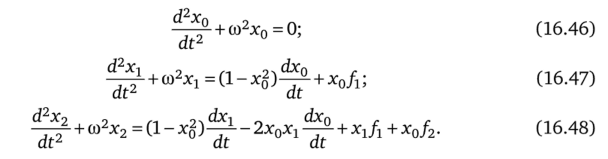
Проинтегрируем (16.46): х₀ =A₀cos wt.

Подставив х₀ в (16.47) и учтя, что sinacos²a = 0,25sina + 0,25sin3a, получим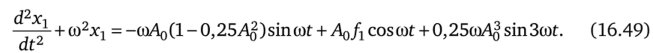

Уравнение (16.49) можно трактовать следующим образом: на колебательный LC-контур без потерь (левая часть уравнения (16.49)) воздействуют вынуждающая сила с угловой частотой со, равной собственной частоте колебательного контура, и сила с угловой частотой, в три раза большей.

Известно, что если подключить колебательный LC-контур, имеющий активное сопротивление R —> 0, к источнику синусоидальной ЭДС E_msin cot при оговоренных условиях, то амплитуда тока в цепи будет нарастать до бесконечности. Действительно,.

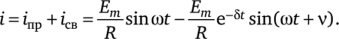
При R —> 0 v-> 0 и 5 = R/(2L)-> 0.

Разложим е~& в ряд и, учитывая малость 8, возьмем два первых члена ряда. ?

В результате получим i ~ sin tot.

Такие члены в решении дифференциальных уравнений, амплитуды которых нарастают теоретически до бесконечности при увеличении времени t, называют вековыми. При дальнейшем решении уравнения (16.49) необходимо помнить о том, что амплитуды вековых членов должны оказаться равными нулю при любом t > 0.

Решение (16.49) запишем следующим образом:

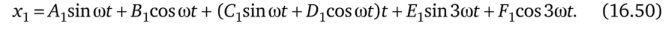
Первое и второе слагаемые представляют собой полное решение однородного уравнения; четвертое и пятое — частное решение неоднородного уравнения. Третье слагаемое представляет собой вековой член. Его можно было бы не вводить в дальнейшие выкладки по определению коэффициентов А_ь В_1з Е_ь F_X, C_V D_b однако введем его, чтобы показать, что его присутствие выкладкам не помешает.

Дважды продифференцируем (16.50) по времени:

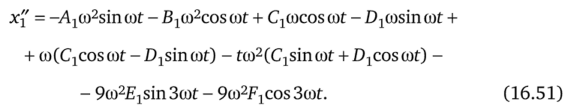
Подставим (16.50) и (16.51) в (16.49), выделим из левой и правой частей (16.49) слагаемые соответственно с sin cot (формула (16.52)), coscot (формула (16.53)), sin3cot (формула (16.54)), cos3cot (формула (16.55)):

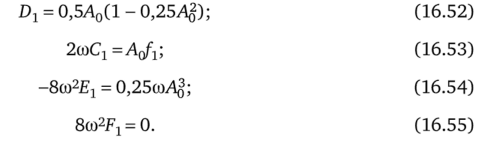
Слагаемые (16.49) с вековыми членами дают нуль:

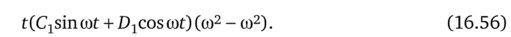
Используем также заданные начальные условия для определения А_ь В_г, С_ь D_b Е_ь F_v Так как начальные условия уже были удовлетворены при определении л:₀, то для всех последующих приближений начальные условия нулевые. Имея это в виду, из (16.50) находим ^(0) -B₁ + F₁ = 0.

В соответствии с (16.55) F_x = 0, поэтому В_г = 0. Из уравнения (16.50), используя условие х{ = 0, получим.

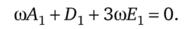
Но Е_г известно из (16.54), поэтому.

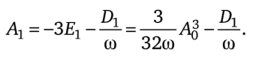
Поправку на угловую частоту/^ а вместе с тем и значение А₀ найдем исходя из того, что амплитуда векового члена должна быть равна нулю при любом f > 0. Отсюда С_г = 0 и D_x = 0.

Из (16.53) следует, что/_г = 0, а из (16.52) — что А₀ = 2.

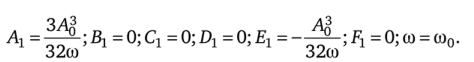
Ограничившись первым приближением и перейдя от р к к_г, получим.

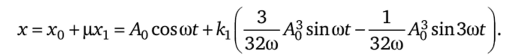
Первое приближение привело к изменению амплитуды первой гармоники.

. _. ₀ L f0,75^?

с Л₀ = 2 до Дэ = 2 J1 +1 —-—- I и к появлению третьей гармоники.

Угловая частота первой гармоники в первом приближении не изменилась и равна угловой частоте ш₀ нулевого приближения. Аналогично производится и второе приближение. Однако каждое последующее приближение по сравнению с предыдущим более трудоемко.

В основу данного метода положены работы французского математика Пуанкаре по небесной механике. Метод называют методом малого параметра, потому что в нем выполняют разложение решения в ряд по степеням малого параметра. Насколько этот параметр должен быть мал в каждом примере, заранее сказать нельзя. Важно, чтобы ряды для х и для о)² или со сходились. Если ряды будут сходиться медленно или вообще не будут сходиться, то пользоваться этим методом не имеет смысла.