Основное уравнение кинетической теории газа

Величину называют кинетической энергией поступательного движения молекулы для того, чтобы отличить ее от той части кинетической энергии молекулы, которая связана с движением атомов внутри нее. Среднее значение энергии поступательного движения молекулы будет.

которое называется уравнением Клаузиуса, или основным уравнением молекулярно-кинетической теории идеального газа. Это — первое соотношение, которое было получено на основе представления о газе как совокупности быстро и хаотически движущихся частиц. Поэтому его называют основным уравнением.

Распределение Максвелла — Больцмана

Рассмотрим идеальный газ, находящийся в состоянии термодинамического равновесия. Функцию (3.6), описывающую распределение молекул газа в пространстве и по скоростям, можно найти при помощи распределения Гиббса. Для этого идеальный газ следует рассматривать как ансамбль, каждая система которого является одной из молекул газа. При этом величину х в формуле (2.35) следует понимать как совокупность пространственных координат х, у, z и проекций v_Xf v_y, и_г вектора скорости молекулы:

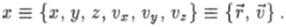
Согласно закону Гиббса (2.35) плотность вероятности для одной из молекул идеального газа, находящегося в состоянии термодинамического равновесия, будет иметь вид.

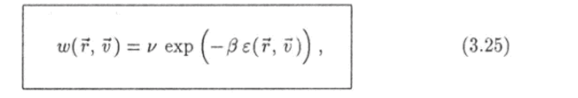
где 0 = (k Т) ¹ — обратная температура,.

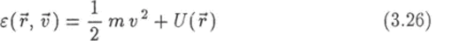
— та часть энергии молекулы, которая зависит от ее координат и скорости, т. е. сумма кинетической энергии поступательного движения молекулы и ее потенциальной энергии U = U®, если в пространстве имеется внешнее поле консервативной силы (например, на молекулы действует сила тяжести). Кроме энергии (3.26), молекула обладает также внутренней энергией, которая принимает дискретные значения. Если молекула состоит более, чем из одного атома, то она может совершать колебательные и вращательные движения. В атоме имеются движущиеся вокруг его ядра электроны. Каждому из этих видов движения соответствуют определенные энергии, которые в сумме и составляют внутреннюю энергию молекулы.

Зная плотность вероятности (3.25), функцию распределения найдем по формуле (3.11):

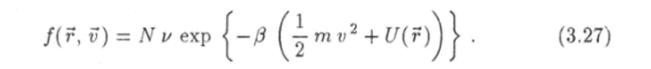
Функции (3.25) и (3.27) носят названия распределений Максвелла — Больцмана (Джеймс Максвелл (1831 — 1879) — английский физик). Одной из характерных особенностей этих функций является то, что они зависят только от модуля вектора скорости и не зависят от его направления в пространстве. Иначе говоря, эти функции описывают изотропное распределение молекул по скоростям.

Функцию распределения (3.27) удобно представить в виде произведения двух функций:

первая из которых.

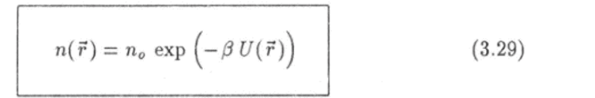
— концентрация молекул, а вторая — плотность вероятности.

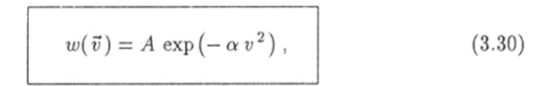
где А — нормировочная постоянная,.

Постоянные п₀ и А связаны соотношением.

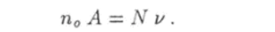
Функцию (3.29) называют распределением Больцмана, а функцию (3.30) — распределением Максвелла. Первая описывает распределение молекул в пространстве, а вторая — их распределение по скоростям.

Подстановка функции (3.28) в равенство (3.9) приводит к условию нормировки для функции (3.30):

Именно в силу этого условия функцию (3.30) следует считать плотностью вероятности распределения молекул по скоростям.

Подстановка функции распределения (3.28) в формулу (3.13) для среднего значения ^ функции дает.

Прежде чем можно будет пользоваться этой формулой, необходимо вычислить постоянную А. Для этого подставим выражение (3.10) и функцию (3.30) под знак интеграла в условии (3.32). С учетом того, что квадрат модуля скорости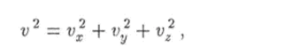

запишем это условие так:

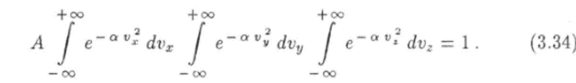
Очевидно, что все три интеграла в левой части этого равенства равны друг другу. Обозначим каждый из них буквой J. Сменив обозначение переменной интегрирования, можно записать.

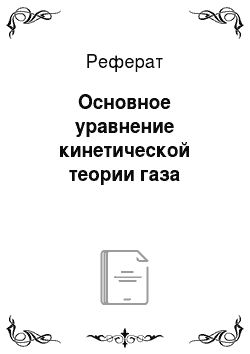
В математике этот интеграл называют интегралом Пуассона (Симеон Пуассон (1781 — 1840) — французский математик и физик).

Используя принятое обозначение (3.35), из условия (3.34) найдем, что.

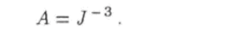
Для отыскания нормировочной постоянной А необходимо вычислить интеграл Пуассона. Вычисления этого интеграла приводят к формуле.