Условия оптимальности для задачи с интегральными связями
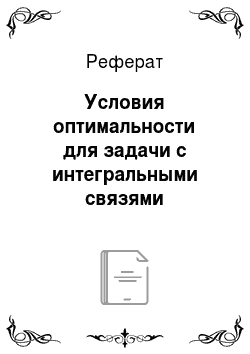
Пусть расширенная задача (4.24), (4.25) имеет решение, отличное от (4.23). При каждом t, как для усредненной задачи НП с т условиями, ее решение Р*(у, t) представляет собой сумму не более чем (m + 1) 6-составляющих с неотрицательными весами, т. е. для каждого t решение у должно принимать базовые значения уе Vy, j = О, …, т, с вероятностями у, — Хотя это решение не соответствует никакой… Читать ещё >
Условия оптимальности для задачи с интегральными связями (реферат, курсовая, диплом, контрольная)
Рассмотрим частный вид вариационной задачи с интегральным функционалом (4.1), связями в форме (4.7) и ограничениями (4.12). При этом кроме функции y (t) задача содержит еще вектор искомых, не зависящих от t параметров z е Vz. Функцию у (О будем искать среди таких кусочно-непрерывных функций, для которых интегралы, входящие в критерий и ограничения, существуют. Задача примет форму юз.
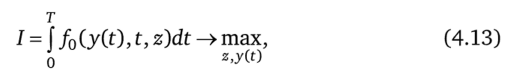
при условиях.
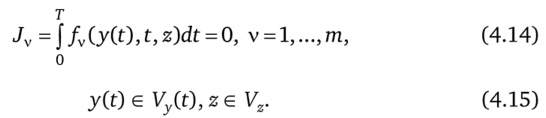
Ограничения на вектор z будем для простоты считать неравенствами, наложенными на каждую его составляющую, т. е. Vz — параллелепипед в векторном пространстве. Если это множество выделяется условиями в форме гладких функций типа (p (z) < 0, читатель без труда внесет изменения в записанные ниже условия оптимальности, так как для любого решния у (0 задача определения z представляет собой задачу НП.
Чтобы сформулировать условия оптимальности задачи, образуем функционал Лагранжа:
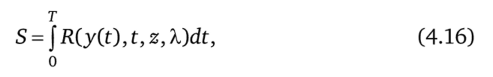
в котором подинтегральное выражение.
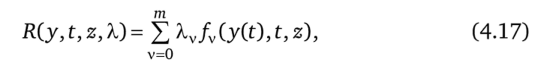
множитель А,0 равен нулю для вырожденного и единице для невырожденного решения. Смысл вырожденного решения здесь тот же, что в задаче НП. Функции/v, v = 0, 1, …, т, непрерывны по совокупности переменных и непрерывно дифференцируемы по z.
Справедлива следующая теорема.
Теорема 4.1. Если решение z*, у*(0 задачи (4.13)—(4.15) в классе кусочно-непрерывных функций существует, то найдется такой ненулевой вектор множителей Лагранжа X, что на этом решении выполнены условия
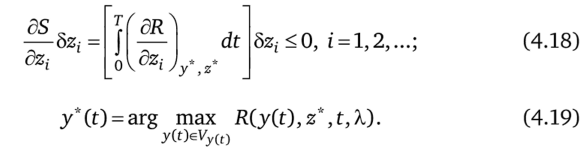
Покажем справедливость соотношений (4.18), (4.19).
Неравенства (4.18) представляют собой просто следствие того, что для каждой фиксированной функции y (t), в том числе и для у*(О, задача (4.16), (4.17) представляет собой по отношению к z задачу НП, а функционал S — функцию Лагранжа этой задачи. Так что неравенства (4.18) вытекают из теоремы Куна — Таккера как условие локальной неулучшаемости функции Лагранжа.
Условия в форме принципа максимума (4.19) так же следовали бы из условий оптимальности для усредненной задачи нелинейного программирования, если бы в функции/о и/у, v = 1, …, т, не входило явно t. Действительно в этом случае задача (4.13)—(4.15) представляла бы собой задачу нелинейного программирования с усреднением по части переменных вида.

Условия (4.18), (4.19) совпадали бы с условиями (3.18) для задачи этого типа, т. е. по тем переменным у, по которым производится осреднение, функция Лагранжа максимальна, а по остальным (детерминированным) переменным z она локально-неулучшаема.
В рассматриваемой задаче t входит явно. Чтобы показать справедливость условий (4.19), проведем расширение множества допустимых решений задачи (4.13)—(4.15) за счет перехода от поиска кусочнонепрерывной функции y (t) к поиску ее вероятностной меры Р (у, t) с заменой функций/у на их средние по у значение. При каждом t функция меры Р (у, t) неотрицательна при любом допустимом значении у, а ее интеграл по множеству всех допустимых значений у (0 равен единице:
причем 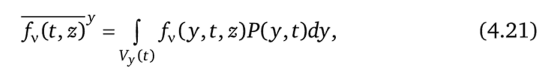
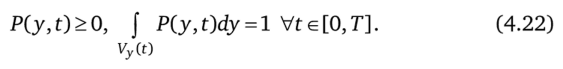
Такой переход расширяет множество допустимых решений задачи, так как каждой кусочно-непрерывной функции y°(t) соответствует Р (у, 0 вида.

При подстановке этой меры в расширенную задачу 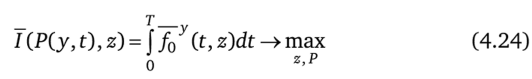 при условиях (4.22) и
при условиях (4.22) и 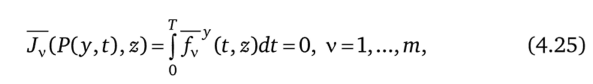
она совпадает с задачей (4.13), (4.15). Однако обратное неверно, т. е. не каждой Р (у, t) соответствует кусочно-непрерывная функция. Например, для меры вида.
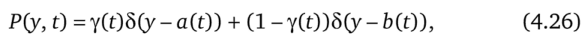
где y (t) > 0, не найдется соответствующей ей кусочно-непрерывной у (t), так как значение у при каждом t с вероятностью у должно быть равно, а (0 и с вероятностью (1 — у) равно b (t).
Требование существования решения в классе кусочно-непрерывных функций, фигурирующее в теореме 4.1, эквивалентно требованию существования решения расширенной задачи (4.24), (4.25) в классе распределений вида (4.23).
Расширенная задача для каждого t и z* представляет собой усред;
неную задачу НПУ и условия оптимальности этой задачи, как показано выше в гл. 3, имеют форму принципа максимума. Значит, если ее решение имеет вид (4.23), то соответствующая функция y°(t) =y*(t) доставляет максимум R при каждом t. Чтобы гарантировать существование этого максимума, нужно потребовать, чтобы Vy(t) было замкнуто и ограничено, а функция R непрерывна по у и ограничена сверху.
Пусть расширенная задача (4.24), (4.25) имеет решение, отличное от (4.23). При каждом t, как для усредненной задачи НП с т условиями, ее решение Р*(у, t) представляет собой сумму не более чем (m + 1) 6-составляющих с неотрицательными весами, т. е. для каждого t решение у должно принимать базовые значения уе Vy, j = О, …, т, с вероятностями у, — Хотя это решение не соответствует никакой кусочно-непрерывной функции, но можно построить последовательность таких функций, каждый следующий член которой со все большей частотой переключался бы между значениями yt. Критерий оптимальности (4.13) исходной задачи стремился бы на такой последовательности к максимальному значению I, а функционалы (4.14) были бы сколь угодно близки к нулю вследствие непрерывности по t функций, входящих в подынтегральные выражения, и усредненного влияния операции интегрирования. Таким образом в этом случае максимума в задаче (4.13)—(4.15) не существует, но существует точная верхняя грань, которая достигается при сколь угодно быстро переключающейся функции у (0 (в скользящем режиме).
Таким образом, любое решение расширенной задачи может быть сколь угодно точно по значению максимизируемого функционала приближено последовательностью решений исходной, так что расширение (4.24), (4.25) эквивалентно исходной задаче (4.13)—(4.15), а значит, необходимые условия оптимальности расширенной задачи являются необходимыми условиями оптимальности решения исходной, если оно существует.
Отметим, что эта эквивалентность не всегда имеет место. Если, например, критерий оптимальности имел бы форму (4.2) или в интетральной записи вид (4.4), то по тем составляющим у (t), которые вошли в/0, расширение для t = т не было бы эквивалентно, так как отсутствует сглаживание скользящего режима при интегрировании.