Использование методов преобразования в некоторых прикладных задачах оптимального управления

Рассмотрим реальные задачи оптимизации и управления и покажем, как могут быть использованы для их решения изложенные выше условия оптимальности и приемы преобразования.

Условия оптимальности и оценки эффективности циклических режимов

Постановка задачи. Пусть динамика системы характеризуется дифференциальными уравнениями.

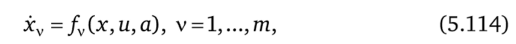
правые части которых явно не зависят от t. Здесь х — переменные состояния, и — управления, а — параметры, подлежащие оптимальному выбору. Краевые условия для уравнений (5.114), как правило, не фиксированы, но на переменные состояния наложены условия цикличности.

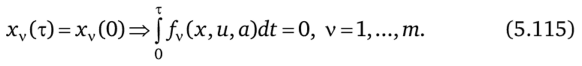
Критерий оптимальности циклического процесса имеет смысл средней за цикл эффективности и может быть записан в форме.

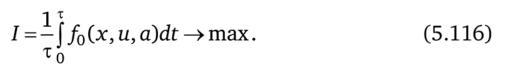
Продолжительность цикла т является одной из составляющих вектора айв общем случае не фиксирована. На параметры и управляющие воздействия наложены ограничения ае У_а, и е V_u; кроме интегральных ограничений (5.114), определяющихся требованием цикличности, в задаче обычно имеются интегральные ограничения, связанные с заданной средней интенсивностью потребления того или иного ресурса (ресурсные ограничения).

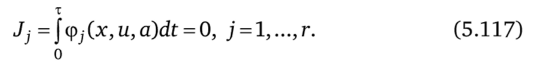
Предполагают, что функции, определяющие задачу, непрерывны по совокупности переменных и непрерывно дифференцируемы по х и а.

Условия оптимальности. Условия оптимальности задачи (5.114) — (5.117) могут быть получены с использованием принципа максимума Понтрягина. А именно, если оптимальное решение х*, а*, и ' существует и не вырождено, то найдутся ненулевой вектор X и дифференцируемая вектор-функция |/(t), такие что функция.

стационарна по х, достигает максимума по и, а интеграл S от этой функции удовлетворяет условиям локальной неулучшаемости по а.

Получим:

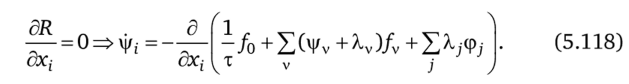
Так как значения х_у(т) и х_у(0) не фиксированы, то |/_у(т) и |/_у(0) равны нулю. Введя обозначения ф_у = р_у + А,_у и учитывая, что ф_у =j/_v, можно переписать условия (5.118) в форме.

Причем для этих уравнений из равенства нулю р (0) и |/(т) вытекают условия цикличности по сопряженным переменным.

Условия максимума Я по и имеют вид.

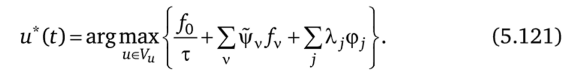
Наконец, условия оптимальности по каждой из составляющих а_к вектора а, к числу которых принадлежит и продолжительность цикла т, приводят к неравенствам.

Здесь 5а — конус допустимых по отношению к включению, а е V_a вариаций вектора а.

Отметим, что фазовая траектория, соответствующая оптимальному циклическому процессу, если решение единственно, не имеет самопересечений. В противном случае каждый ее замкнутый участок соответствовал бы оптимальному циклу.

Оценка эффективности перехода к циклическому процессу.

Условия эквивалентности и эффективности циклического расширения.

Задача (5.114)—(5.117) об оптимальном циклическом режиме (назовем ее задачей Ц) представляет собой расширение задачи нелинейного программирования. Действительно, в том случае, когда на решение этой задачи наложены дополнительные условия х = const, и = const, получим задачу об оптимальном статическом режиме (задачу С):

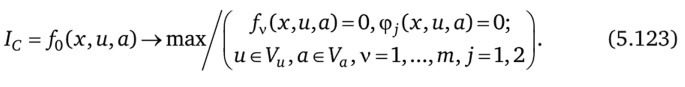
Так как множество допустимых решений задачи (5.114)—(5.117) шире, чем множество допустимых решений задачи С, то.

где через 7ц обозначено значение задачи об оптимальном циклическом процессе.

Одной из проблем проектирования циклических процессов является получение условий, позволяющих выявить класс задач, для которых неравенство (5.124) превращается в равенство, т. е. циклическое расширение эквивалентно. Важную роль при решении этой задачи играет функция Лагранжа задачи С.

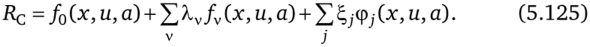
Для ответа на вопрос об эквивалентности или эффективности циклического процесса без решения задачи (5.114)—(5.117) образуем усредненные задачи, являющиеся в свою очередь расширениями для задачи С или Ц или для той и другой. Сравнение значений этих задач с величиной 7ц позволяет найти условия эквивалентности циклического расширения.

Оценка величины 7ц сверху и достаточные условия эквивалентности циклического расширения. Расширим множество допустимых решений задачи Ц, отбросив дифференциальные уравнения (5.114). В этом случае мы получим задачу С, которую будем называть оценочной:

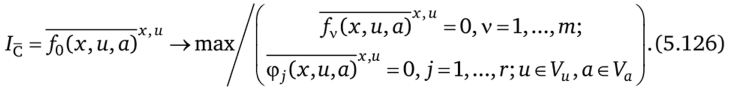
Ясно, что.

а задача С представляет собой усредненное расширение для задачи С, содержащее переменные х, и и параметры а. При этом х ии входят в условия задачи С равноправно, и их можно объединить, обозначив как у = (х, и). В сокращенной записи эта задача примет форму.

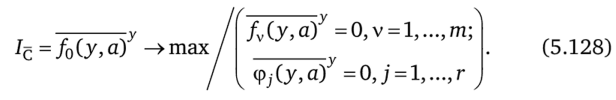
Значение задачи (5.128) как расширения задачи об оптимальном статическом режиме может быть выражено через функцию R_c как.

Для определения вектора параметров имеем условие.

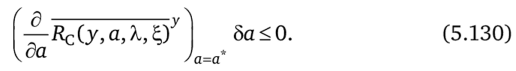
В том случае, когда а* лежит внутри V_a, условие (5.130) сводится к условию стационарности R_c по а.

Если найденное по формуле (5.129) значение I^ равно Iq, а этому соответствует случай, когда задача С имеет единственное базовое решение, то из неравенств (5.124) и (5.127) следует, что 7ц =/?, т. е. статический режим нельзя улучшить за счет перехода к циклическому режиму. Если же > Iq, то разница между ними Д_с дает верхнюю оценку того выигрыша, который возможен при переходе к циклическому режиму.

Оценка величины 7ц снизу. Квазистатические и скользящие режимы. Рассмотрим случай, когда изменения x (t) и и (7) таковы, что производными x (t) по времени можно пренебречь, так что связи х и и определяются так же, как и в статике, — зависимостями /(x (t), u (t), a) = = 0 Vt. Соответствующий режим называют квазистатическим. Задача об оптимальном выборе x (t), u (t) при условиях квазистатики (задача КС) имеет форму.

или в сокращенной записи.

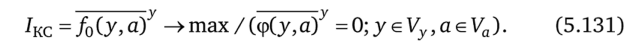
Здесь у = (х, и), а множество V_y определяется включениями и е V_u, а е е V_a и условиями/(х, и, а) = 0.

Так как любое решение задачи КС допустимо в задаче Ц, то справедливо неравенство.

В то же время значение 7Д задачи КС как значение усредненной задачи определяется выражением.

Здесь а* — оптимальное значение вектора а, удовлетворяющее условию.

в котором 5а — множество вариаций, допустимых по включению.

а е У_а.

Множители Лагранжа X¹ в (5.134) выбирают так, чтобы для любого базового значения у' вектора у были выполнены условия/(у', а) = 0. Число базовых значений у определяется размерностью г вектор-функции ф, так что задача принимает форму.

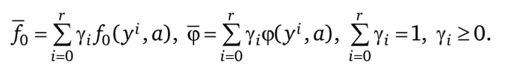
Рассмотрим случай, когда изменения вектора управления происходят со столь большой частотой, что вектор состояния х практически постоянен. Подобный режим называют скользящим установившимся режимом. Сформулируем задачу оптимизации такого режима как.

Эту задачу называют задачей СК. Через Ь в (5.135) обозначен вектор с составляющими х и а. Этот режим является предельным случаем циклического, так что справедливо неравенство.

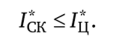
Задача (5.135) представляет собой усредненное расширение задачи С с двумя типами переменных; ее значение:

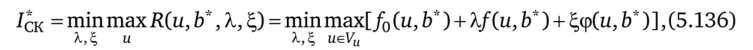
при этом вектор Ь* удовлетворяет условию.

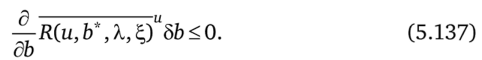
Число базовых значений вектор-функции и в задаче СК не превосходит m + r + 1.

Необходимое условие целесообразности перехода к циклическому режиму может быть сформулировано через 7^с ^искДля этого введем величину.

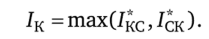
Если величина /_к больше, чем Iq, то переход к циклическому режиму эффективен, а разность Д_к = 1_К — Iq оценивает эту эффективность снизу.

Частотный критерий целесообразности перехода к циклическому режиму. Будем предполагать, что оптимальный статический режим х°, и⁰ в задаче С найден. Требуется, как и выше, определить, эффективно ли циклическое расширение задачи. Предложен¹ частотный критерий целесообразности циклического режима. Этот критерий основан на исследовании приращения критерия оптимальности I по отношению к его максимальному статическому значению 1° при малых гармонических колебаниях управления относительно и⁰.

Пусть Л° и ц° — значения множителей Лагранжа Лир, соответствующих оптимальному статическому режиму, в функции Лагранжа для задачи С.

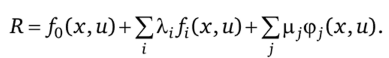
В окрестности оптимального статического режима и соответствующих ему множителей Лагранжа вычислим первые и вторые производные по х и и функций, определяющих задачу (эти производные для случая, когдахи и — векторы, представляют собой матрицы):

Приращение функционала I при малых вариациях 8x (t) и 8u (t) в окрестности оптимального статического режима можно выразить как.

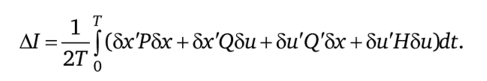
Вопрос о целесообразности перехода к циклическому режиму сводится к определению такой вариации 8п, для которой величина AI была бы положительна при линеаризованных условиях (5.114):

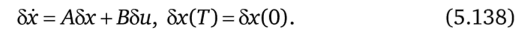
Чтобы освободиться от этих связей, сузим класс вариаций до гармонических:

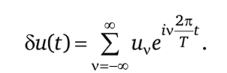
Guardabassi G., Locatelli A, Rinaldi S. Periodic optimization of continuous systems //.

Proc. Int. Conf. Cubern and Soc. Washington, D. C., 1972. P. 261—263.

Преобразовав по Фурье линейные дифференциальные связи (5.138), получим.

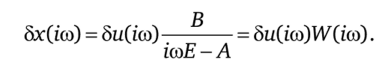
Здесь Е — единичная матрица (если х — скаляр, то Е = 1). Кроме того, предполагают, что матрица А не имеет собственных значений с нулевой действительной частью, иначе малым отклонениям 8u (t) могли бы соответствовать большие отклонения 8x (t) и проведенная линеаризация не была бы правомерна.

Если величину АI выразить по формуле Парсеваля в частотной области, подставив вместо 8x (ico) его выражение через 8п, то приращение критерия при гармонических колебаниях управления с частотами, кратными 2п/Т, примет вид.

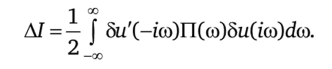
Здесь П (оо) определяется матрицами Р, Q, Н и связью между 8п и 5х и, как нетрудно показать, имеет форму.

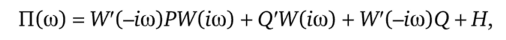
где штрих обозначает транспонирование.

Для скалярной задачи.

Критерий целесообразности перехода к циклическому режиму утверждает, что если для некоторого значения со матрица П (со) такова, что подынтегральное выражение в функционале AI положительно хотя бы для одного вектора 5и, то статический режим может быть улучшен.

Так как для скалярной задачи.

то статический режим улучшается, если для некоторого со величина П (со) больше нуля.

Ляпуновские и приводящиеся к ним задачи. Для важного класса задач неравенство (5.127) превращается в равенство. В этих задачах функции/₀,/и ф в соотношениях (5.114)—(5.117) зависят только от и и а, так что уравнения (5.114) примут вид ляпуновских:

Отбрасывая в задаче Ц уравнения (5.114), имеющие вид (5.139), и переходя тем самым к задаче С, можно найти ее решение u*(t), а*. Подстановка этого решения в уравнения (5.139) определяет оптимальную траекторию. Ясно, что для этой задачи I^ - /ц, при этом оптимальное управление и* (0 принимает не более чем т + г + 1 базовых значений, а функция х* (0 представляет собой ломаную, имеющую не более чем т + r точек излома.

К ляпуновским могут быть приведены задачи, в которых наряду с уравнениями ляпуновского типа могут присутствовать уравнения вида.

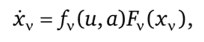
которые приводятся к форме (5.139) посредством замены переменной.

так что y_v = /_v(u, а). Оптимальное решение y*(t) кусочно-линейное, a x_v(t) определяют из (5.140) как решение уравнения.