Точное решение задачи

Мы будем рассматривать функционалы, определенные на некотором множестве дифференцируемых, функций. Сами эти функции мы можем считать элементами пространства С или пространства D1. В соответствии с этими двумя возможностями мы будем говорить, что функционал достигает при слабого экстремума, если существует такое что сохраняет постоянный знак для всех тех у из D1 для которых функционал определен… Читать ещё >
Точное решение задачи (реферат, курсовая, диплом, контрольная)
Уравнение Эйлера
Пусть — дифференцируемая функция n переменных. Говорят, что имеет в точке экстремум, если.
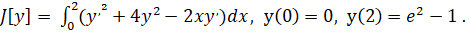
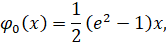
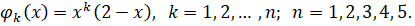
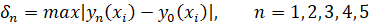
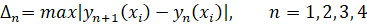
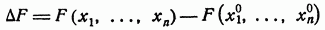
имеет один и тот же знак для всех точек принадлежащих некоторой окрестности точки именно F имеет в данной точке минимум, если в данной окрестности, и максимум в случае .
Аналогично мы скажем, что функционал достигает экстремума при если сохраняет знак в некоторой окрестности кривой.
Мы будем рассматривать функционалы, определенные на некотором множестве дифференцируемых, функций. Сами эти функции мы можем считать элементами пространства С или пространства D1. В соответствии с этими двумя возможностями мы будем говорить, что функционал достигает при слабого экстремума, если существует такое что сохраняет постоянный знак для всех тех у из D1 для которых функционал определен и означает норму в пространстве D1 будем называть значение сильным экстремумом, если оно является экстремальным по отношению ко всем тем y (x) которые принадлежат области определения функционала и удовлетворяют условию (т. е. близки к y0 в смысле нормы пространства С).
Ясно, что всякий сильный экстремум будет в то же время и слабым экстремумом.
Действительно, если то подавно поэтому если есть экстремум по отношению ко всем у таким, что в, то тем более будет экстремумом по отношению к тем у, для которых Обратное, вообще говоря, неверно, т. е. слабый экстремум может сильным экстремумом и не быть. Нахождение слабого экстремума является, как правило, задачей более простой, чем нахождение сильного экстремума. Причина этого состоит в том, что, как было отмечено в конце предыдущего параграфа, функционалы, рассматриваемые обычно в вариационном исчислении, непрерывны в пространстве D1. Поэтому в теории слабого экстремума можно пользоваться непрерывностью функционалов. В то же время эти функционалы, вообще говоря, не непрерывны по отношению к норме пространства С.
Теорема. Для того чтобы функционал при достигал экстремума, необходимо, чтобы его дифференциал если он существует) обращался в нуль при т. е.
Доказательство. Рассмотрим для определенности случай минимума. Если при достигает минимума, то это значит, что для всех h, для которых, достаточно мала. Но, по определению вариации,.
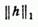
и при. Если, то при достаточно малых h знак выражения.
(1.1.1).
определяется знаком первого (главного) члена. Но — линейный функционал, поэтому и, следовательно, при выражение (1.1.1) может быть как положительным, так и отрицательным при сколь угодно малых h, т. е. экстремум в этом случае невозможен.
Изучение конкретных задач вариационного исчисления мы начнем с так называемой простейшей задачи, которая формулируется следующим образом. Пусть F (x, y, z) — функция, имеющая непрерывные частные производные по всем переменным до второго порядка включительно. Среди всех функций y (x) имеющих непрерывную производную и удовлетворяющих условиям.
(1.1.2).
найти ту функцию, которая доставляет слабый экстремум функционалу.
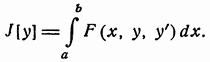
(1.1.3).
Иначе говоря, простейшая задача вариационного исчисления состоит в отыскании слабого экстремума функционала вида (1.1.3) на множестве всех гладких кривых, соединяющих две заданные точки.
Чтобы применить к решению сформулированной простейшей задачи необходимое условие экстремума, нужно уметь вычислять вариацию для функционалов вида (1.1.3). Выведем соответствующую формулу.
Дадим функции у (х) некоторое приращение h (x) Для того чтобы функция по-прежнему удовлетворяла граничным условиям, нужно, чтобы Вычислим приращение функционала (1.1.3). Оно равно.
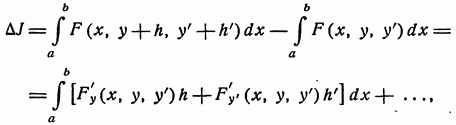
где многоточие обозначает члены порядка выше первого относительно h и h'. Выражение.
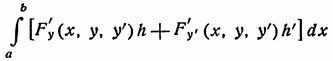
представляет собой главную линейную часть приращения? J функционала J, т. е. дифференциал.
Необходимым условием экстремума является равенство.
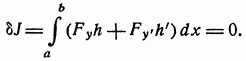
(1.1.4).
из равенства (1.1.4) вытекает, что.
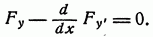
(1.1.5).
Выражение (1.1.5) называется уравнением Эйлера.
Таким образом, установлена следующая Теорема 1:
Для того чтобы функционал.
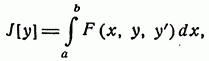
определенный на множестве функций y = y (x) имеющих непрерывную первую производную и удовлетворяющих условиям y (a) = A, y (b) = B, достигал на данной функции y (x) экстремума, необходимо, чтобы эта функция удовлетворяла уравнению Эйлера.
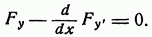
Интегральные кривые уравнения Эйлера называются экстремалями.
Уравнение Эйлера представляет собой дифференциальное уравнение второго порядка. Его решение должно зависеть, вообще говоря, от двух произвольных постоянных, которые определяются из двух краевых условий y (a) = A, y (b) = B.
При решении уравнения Эйлера ищется решение, определенное во всей фиксированной области и удовлетворяющее заданным граничным условиям. Поэтому вопрос о разрешимости той или иной вариационной задачи не сводится непосредственно к обычным теоремам существования для дифференциальных уравнений.
Приведем следующую теорему С. Н. Бернштейна о существовании и единственности решения в целом для уравнения вида.
(1.1.6).
Если функции F, Fy,Fy' непрерывны в каждой конечной точке (x, y) для любого конечного у' и если существует такая постоянная k>0 и такие, ограниченные в каждой конечной части плоскости функции что.
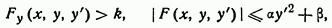
то через любые две точки (a, a1) (b, b1) плоскости (x, y) абсциссы которых различны (a не равно b), проходит одна и только одна интегральная кривая уравнения (1.1.6).
Эйлера дает исчерпывающее решение задачи. Действительно, часто само существование экстремума бывает ясно из физического или геометрического смысла задачи (например, задачи о брахистохроне, о кратчайшем расстоянии между двумя точками и т. п.). Если при этом существует лишь единственная экстремаль, удовлетворяющая граничным условиям задачи, то именно она и будет непременно той кривой, которая реализует искомый экстремум.
Уравнение Эйлера для функционала представляет собой уравнение второго порядка. Может оказаться, однако, что та кривая, на которой этот функционал достигает экстремума, является дважды дифференцируемой. Рассмотрим, например, функционал.
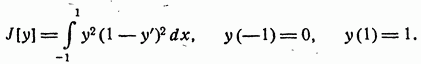
Его минимальное значение, равное нулю, достигается на функции.
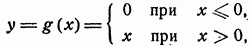
не имеющей второй производной. Хотя функция g (x) и не имеет второй производной, она удовлетворяет соответствующему уравнению Эйлера. Действительно, при F (x, y, y') =y2(1-y') и y=g имеем и, следовательно, и хотя уравнение Эйлера имеет порядок два, g"(x) не существует, подстановка g (x) в уравнение Эйлера обращает его в тождество.
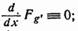
Выясним теперь условия, при, которых можно гарантировать существование второй производной у функции y = y (x) представляющей собой решение уравнения Эйлера.
Теорема 2. Пусть y=y (x) — решение уравнения Эйлера. Если функция F (x, y, y') имеет непрерывные частные производные до второго порядка включительно, то во всех точках (x, y) в которых.
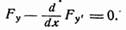
функция у = у (х) имеет непрерывную вторую производную. Доказательство. Рассмотрим разность.
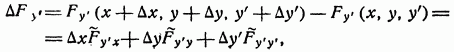
где знак ~ указывает, что производные берутся в некоторой промежуточной точке.
Разделив эту разность на? x рассмотрим предел полученного выражения при? x->0 (этот предел существует, так как Fy' имеет производную по х, в силу уравнения Эйлера она равна Fy).
Так как вторые производные функции F (x, y, y') по условию непрерывны, то при? x->0 стремится к т. е. к значению производной в точке x.
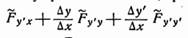
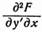
Второе слагаемое, т. е. при? x->0 также имеет предел. Это вытекает из существования у' и непрерывности второй производной Fyy'. Но тогда существует предел и третьего слагаемого (так как предел всей суммы существует), т. е. существует.
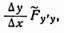
Если ?x->0 то стремится к пределу, и значит, существует.
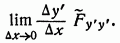
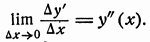
Из уравнения.
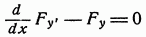
можно найти выражение для y" из которого видно, что у" непрерывна всюду, где. Теорема доказана.
Из этой теоремы вытекает, что экстремаль может иметь излом только в тех точках, где.
- 2. Уравнение Эйлера, выведенное нами в этом параграфе, играет фундаментальную роль во всем вариационном исчислении. Оно представляет собой, вообще говоря, дифференциальное уравнение второго порядка. Укажем некоторые частные случаи, в которых это уравнение может быть сведено к уравнению первого порядка или даже полностью проинтегрировано в квадратурах.
- 1. Подынтегральная функция не зависит от у. Предположим, что рассматриваемый функционал имеет вид
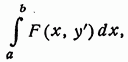
т. е. F не содержит у явно. В этом случае уравнение Эйлера принимает вид.
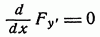
и имеет, очевидно, первый интеграл Это — уравнение первого порядка, не содержащее у. Решив его относительно у, получаем соотношение вида откуда у находится квадратурой.
2. Подынтегральная функция не зависит от х, т. е.
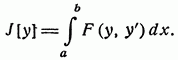
В этом случае.
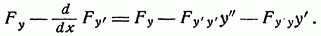
Умножив это выражение на у, получим выражение, которое можно записать в виде.
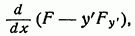
откуда получаем, что в рассматриваемом случае уравнение Эйлера имеет первый интеграл.
3. Если F не зависит от у, то уравнение Эйлера принимает вид.
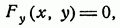
т. е. представляет собой не дифференциальное, а конечное уравнение, определяющее одну или несколько кривых.
4. В различных задачах часто встречаются функционалы вида.
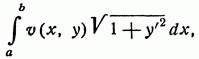
представляющие собой интеграл от некоторой функции v (x, y), взятый по длине дуги. В этом случае уравнение Эйлера может быть преобразовано следующим образом:
т. е.
Решение уравнение Эйлера
Решение уравнения Эйлера в моей задаче необходимо для нахождения точного решения, т. е. единственной экстремали.
Общий вид уравнения Эйлера:
(1.2.1).
Тогда в моем случае уравнение Эйлера будет иметь вид:
8y — 2y" + 2 = 0.
Решение однородного уравнения:
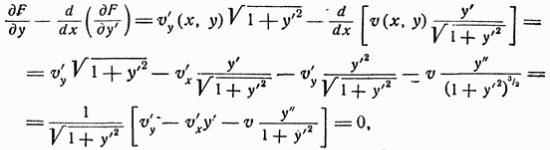
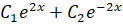
Частное решение уравнения: -0.25.
Общее решение уравнения:
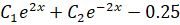
При подстановке краевых условий получаем.
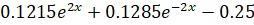
— единственная экстремаль задачи.