Степенные средние величины

Средняя арифметическая величина.

Средней арифметической величиной называется такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным.

Иначе можно сказать, что средняя арифметическая величина — среднее слагаемое. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности.

Средняя арифметическая — наиболее распространенный на практике вид средних. Различают 2 вида арифметических средних:

• · Невзвешенную (простую);
• · Взвешенную.

Средняя арифметическая невзвешенная рассчитывается для несгруппированных данных по формуле:

.

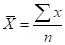
Для массовых статистических совокупностей рассчитывается взвешенная средняя арифметическая по формуле:

.

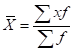
Если при группировке значения осредняемого признака заданы интервалами, то при расчете средней арифметической величины в качестве значения признака в группах принимают середины этих интервалов, т. е. исходят из гипотезы о равномерном распределении единиц совокупности по интервалу значений признака. Для открытых интервалов в первой и последней группе, если таковые есть, значения признака надо определить экспертным путем исходя из сущности, свойств признака и совокупности. Например, по табл. 2.4 можно минимальный возраст рабочих считать 17 лет. Тогда первый интервал будет от 17 до 20 лет, а максимальный возраст — 65 лет, тогда последний интервал — 50−65 лет.

Таблица 2.4. Распределение рабочих предприятия по возрасту.

Средний возраст рабочих, рассчитанный по формуле с заменой точных значений признака в группах серединами интервалов, составил:

= ,.

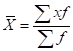
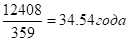
что и записано в итоговую строку по графе 3 табл. 2.4.

Средняя арифметическая величина обладает рядом свойств, позволяющих ускорить расчет:

1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т. е. .

Это свойство определено требованиями правильного исчисления средней, согласно которым конкретные значения варьирующего признака уравниваются без изменения общего объема его и заменяются одним средним числом, которое как постоянный множитель выносится из-под знака суммы. Благодаря этому свойству средняя может быть использована для разного рода плановых и статистических расчетов как представитель или заменитель всех значений варьирующего признака. Так, если средний расход горючего на 1 гектар пахоты составляет 20 литров, а всего надо вспахать 2 млн. га, то всего потребуется 40 млн. литров горючего. Аналогично, если достаточно репрезентативное выборочное обследование показало, что среднегодовой надой молока на одну корову составляет 2500 литров, а всего в районе 15 тыс. коров, то общий надой составит 37,5 млн. литров.

2. Сумма отклонений вариантов как от простой, так и от взвешенной средней арифметической равна нулю:

и.

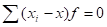
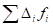
Рассмотренное свойство может быть использовано для проверки правильности исчисления средней. Если при исчислении средней арифметической и не равны нулю, это указывает, что средняя неправильно исчислена. А так как в анализе часто приходится пользоваться отклонениями от средней, их удобно использовать и для проверки правильности исчисления средней.

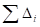
3. Сумма квадратов отклонений вариантов как от простой, так и от взвешенной средней меньше суммы квадратов отклонений от любой другой произвольной величины а, т. е.

.

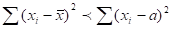
Пример:

Таблица 2.5.

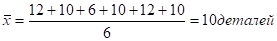
В примере, основанном на данных табл. 2.1.2,, а.

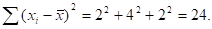
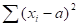
При, а =12 составит:

Таблица 2.6.

Как видим, 24<48.

4. Если все частоты разделить (или умножить) на произвольное число (а), то средняя от этого не изменится, так как:

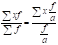
Если разгруппировать рабочих по числу выработанных за час деталей, получим такие данные:

Таблица 2.7.

Если применить полученную формулу, к примеру, приведенному в табл. 8, это означает, что если, например, частоты уменьшить в 6 раз, средняя взвешенная арифметическая не изменится и будет равна:

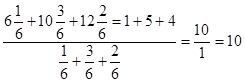
Средняя не изменится, если мы частности выразим в процентах, т. е. умножим их на 100:

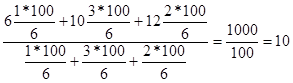
Рассматриваемое свойство показывает, что при данных вариантах признака величина средней зависит не от абсолютного размера весов, а от соотношения между ними. В приведенном примере мы сначала частоты уменьшили в 6 раз, а затем увеличили в 100 раз, но средняя выработка не изменилась.

5. Если веса всех вариантов равны между собой, то взвешенная средняя равна простой средней, так как при этих условиях.

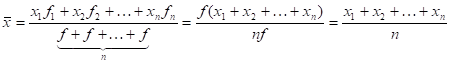
Так как исчисление простой арифметической средней требует меньше затрат труда, чем взвешенной, то при равенстве весов нет надобности пользоваться последней.

6. Средняя алгебраической суммы равна алгебраической сумме средних. Так, если у, х и z — положительные варьирующие величины и уi =xi +zi, то:

.

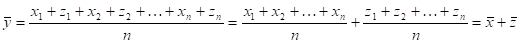
Следовательно, .

Это свойство средней показывает, в каких случаях можно непосредственно суммировать средние. Например, если изделие состоит из двух деталей, изготовляемых разными рабочими, и при этом один из них тратит в среднем на одну деталь 20, а на другую 30 минут, то в среднем на одно изделие расходуется 20 + 30 = 50 минут. Аналогично решался бы вопрос, если бы изделие состояло из трех и более деталей.

Средняя гармоническая величина. Если по условиям задачи необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней. Средняя гармоническая величина, как и средняя арифметическая может быть простой и взвешенной. Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую:

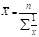
Однако в статистической практике чаще применяется средняя гармоническая взвешенная:

.

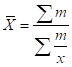
где m = xf,.

она используется, как правило, при расчете общей средней из средних групповых.

Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности — носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т. д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.

Приведем расчет средней гармонической величины — простой и взвешенной.

Пример. Четыре швеи-надомницы заняты пошивом головных уборов одной модели. Первая швея тратит на изготовление одного головного убора 30 мин, вторая — 40 мин, третья — 50 мин, четвертая — 60 мин. Определим средние затраты времени на пошив одного головного убора при условии, что каждая швея работает по 10 ч в день.

Попытка решить задачу с помощью средней арифметической простой.

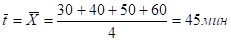
оказалась бы успешной, если бы каждая надомница шила только по одному головному убору в день. В данном же случае средние затраты времени на пошив одного головного убора можно подсчитать делением общих затрат времени на пошив всех головных уборов (600 + 600 + 600 + 600 = 2400 мин) на количество сшитых головных уборов.

Количество головных уборов, сшитых каждой надомницей, равно:

1) 600/30 = 20 шт.; 2) 600/40 =15 шт.; 3) 600/50 = 12 шт.; 4) 600/60 = 10 шт. Всего 57 изделий.

Средние затраты времени вычислим по формуле средней гармонической взвешенной:

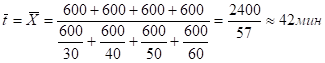
т.е. на пошив одного головного убора тратится в среднем 42 мин.

В качестве веса в этой задаче был принят показатель общих затрат времени на пошив всех головных уборов одной швеей.

Так как в этом примере общие затраты времени у всех надомниц одинаковы, то к аналогичному результату приводит и расчет по формуле средней гармонической простой:

.

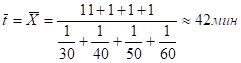
Средняя геометрическая величина.

Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину.

Ее формула такова:

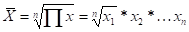
для простой.

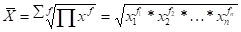
для взвешенной.

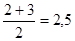
Основное применение геометрическая средняя находит при определении средних темпов роста. Пусть, например, в результате инфляции за первый год цена товара возросла в 2 раза к предыдущему году, а за второй год еще в 3 раза к уровню предыдущего года. Ясно, что за два года цена выросла в 6 раз. Каков средний темп роста цены за год? Арифметическая средняя здесь непригодна, ибо если за год цены возросли бы в раза, то за два года цена возросла бы в 2,5×2,5 = 6,25 раза, а не в 6 раз. Геометрическая средняя дает правильный ответ: v6 — 2,45 раза.

Геометрическая средняя величина дает наиболее правильный по содержанию результат осреднения, если задача состоит в нахождении такого значения признака, который качественно был бы равно удален как от максимального, так и от минимального значения признака. Например, если максимальный размер выигрыша в лотерее составляет миллион рублей, а минимальный — сто рублей, то какую величину выигрыша можно считать средней между миллионом и сотней? Арифметическая средняя явно непригодна, она составляет 500 050 руб., а это, как и миллион, крупный, а никак не средний выигрыш; он качественно однороден с максимальным и резко отличен от минимального. Не дают верного ответа ни квадратическая средняя (707 107 руб.), ни кубическая (793 699 руб.), ни гармоническая средняя (199,98 руб.), слишком близкая к минимальному значению. Только геометрическая средняя дает верный с точки зрения экономики и логики ответ: Десять тысяч — не миллион, и не сотня! Это, действительно, нечто среднее между ними.

Наиболее часто формулу средней геометрической используют для определения средних валютных курсов, эффективности валютных курсов, реальной эффективности валютных курсов (международная финансовая статистика).

Средняя квадратическая величина.

ри замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.

Ее формула такова:

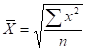
для простой.

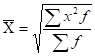
для взвешенной.

Например, имеются три участка земельной площади со сторонами квадрата: х1 = 100 м; х2 = 200 м; х3 = 300 м. Заменяя разные значения длины сторон на среднюю, мы очевидно, должны исходить из сохранения общей площади всех участков. Арифметическая средняя величина (100 + 200 + 300):3 = 200 м не удовлетворяет этому условию, так как общая площадь трех участков со стороной 200 м была бы равна: 3*(200 м)2 =120 000 м2. В то же время площадь исходных трех участков равна: (100 м)2 + (200 м)2 + (300 м)2 = 140 000 м2. Правильный ответ дает квадратическая средняя:

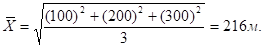
Формула средней квадратической используется для измерения степени колеблемости индивидуальных значений признака вокруг средней арифметической в рядах распределения. Так, при расчете показателей вариации среднюю вычисляют из квадратов отклонений индивидуальных значений признака от средней арифметической величины.

Средняя кубическая величина.

Если по условиям задачи необходимо сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, мы приходим к средней кубической, имеющей вид:

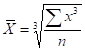
для простой.

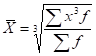
для взвешенной.

Средняя кубическая имеет ограниченное применение в практике статистики. Ею пользуются для исчисления средних диаметров труб, стволов и т. п., необходимых для разного рода расчетов, как, например, для определения.