Эконометрика и экономико-математические методы и модели

Задание 1

При изучении зависимости у = f (x1, x2, x3) по 30 наблюдениям получена матрица парных коэффициентов корреляции.

регрессия мультиколлинеарность фишер издержки.

Определить:

Какие факторы следует включить в модель множественной регрессии и почему?

Проверить наличие мультиколлинеарности факторов, используя определитель матрицы коэффициентов парной корреляции.

Решение:

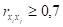
Коэффициенты интеркорреляции (то есть корреляции между факторами из модели множественной регрессии) позволяют исключить из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, то есть находятся между собой в тесной линейной зависимости, если .

Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, то коллинеарность нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, имеющему более тесную связь с результирующим показателем, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

В рассматриваемой задаче.

Следовательно факторы x1 и x3 дублируют друг друга. Связь фактора x3 с результатом у сильнее, чем x1 с результатом у, и в модель включаем именно фактор x3, так как при тесной связи с результатом y этот признак имеет более слабую межфакторную корреляцию с оставшимся фактором x2 .

Таким образом, в модель включаются факторы x2 и x3.

Если более чем два фактора связаны между собой линейной зависимостью, то есть имеет место совокупное воздействие факторов на результат, то говорят о наличии мультиколлинеарности факторов. Такое наличие может означать, что некоторые факторы всегда будут действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами.

Чем ближе к нулю определитель матрицы парных коэффициентов корреляции между факторами, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.

Вычислим определитель (детерминант) матрицы межфакторной корреляции для рассматриваемой задачи:

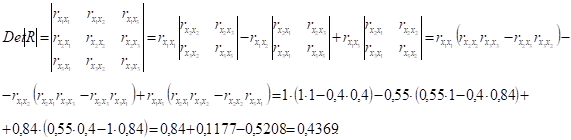
Так как определитель матрицы парных коэффициентов корреляции между факторами равен 0,4369, то факторы имеют среднюю степень мультиколлинеарности.

Задание 2.

По 20 коммерческим банкам изучается зависимость прибыли у (млн. ден. ед.) от кредитных вложений х1 (млн. ден. ед.) и суммарного риска х2 (млн. ден. ед.).

Требуется:

Оценить показатели вариации каждого признака и сделать вывод о возможностях применения метода наименьших квадратов (МНК) для их изучения.

Проанализировать линейные коэффициенты парной и частной корреляции.

Написать уравнение множественной регрессии.

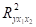
С помощью F-критерия Фишера оценить статистическую надежность уравнения регрессии и. Сравнить значения скорректированного и нескорректированного линейных коэффициентов множественной детерминации.

С помощью частных F-критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора х1 после х2 и фактора х2 после х1. Оценить значимость параметров уравнения множественной регрессии и пояснить их экономический смысл.

Рассчитать средние частные коэффициенты эластичности и дать на их основе сравнительную оценку силы влияния факторов на результат.

Решение:

Для нахождения показателей вариации составим и заполним расчетную таблицу:

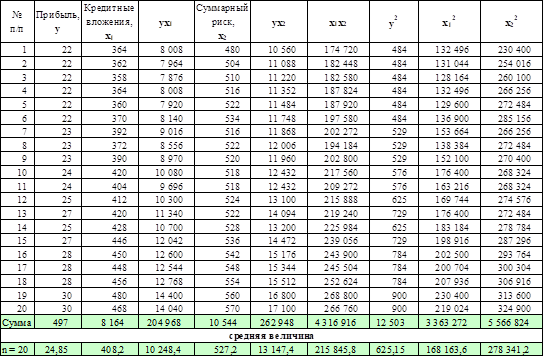
Находим дисперсии и исправленные средние квадратические отклонения признака результата у и признаков факторов х1 и х2:

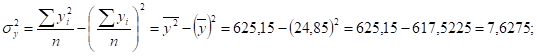
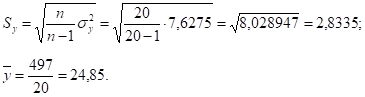
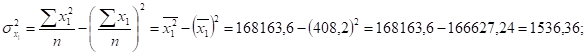
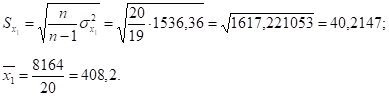
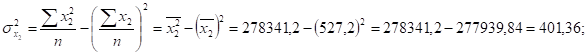
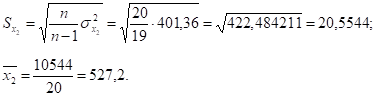
Сравнивая значения средних квадратических отклонений и средних величин и определяя коэффициенты вариации,.

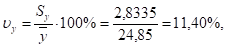
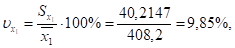
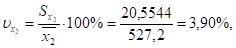
приходим к выводу о небольшом уровне варьирования признаков в пределах 11,4%. Таким образом, совокупность предприятий однородна, и для нее могут использоваться метод наименьших квадратов и вероятностные оценки статистических гипотез.

Значения линейных коэффициентов парной корреляции определяют тесноту попарно связанных переменных, используемых в данном уравнении множественной регрессии. Линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

Для вычисления коэффициентов парной корреляции используем данные вышеуказанной расчетной таблицы:

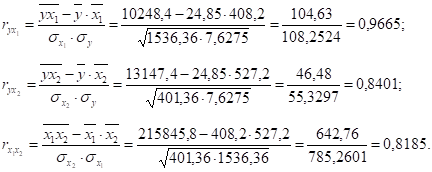
Значения коэффициентов парной корреляции указывают на сильную связь прибыли банков у как с кредитными вложениями х1, так и с суммарным риском х2 (и). В то же время теснота межфакторной связи хотя и достаточно высока, однако ее значение меньше тесноты связи у с х2 и у с х1. В связи с этим можно заключить, что для данной модели факторы х1 и х2 информативны и достаточно статистически надежны.

Линейные коэффициенты частной корреляции (первого порядка):

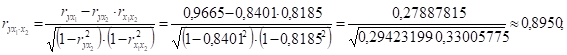
то есть при закреплении фактора x2 на постоянном уровне корреляция у и фактора x1 оказывается более низкой (0,8950 против 0,9665).

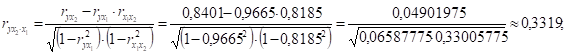
то есть при закреплении фактора x1 на постоянном уровне влияние фактора x2 на у снижается более чем в 2,5 раза (0,3319 против 0,8401).

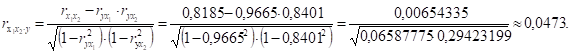
Данные коэффициенты дают более точную характеристику тесноты связи двух признаков, чем коэффициенты парной корреляции, так как очищают парную зависимость от взаимодействия данной пары признаков с другими факторами, представляемыми в модели. Наиболее тесно связаны у и x1: (зависимость прямая); связь у и x2 гораздо слабее: (зависимость также прямая); межфакторная связь x1 и x2 также прямая, при этом она слабая и меньше, чем парная у с x1 и у с x2:

> >. Все это подводит нас к логическому заключению о том, что факторы x1 (кредитные вложения) и x2 (суммарный риск) должны быть включены в правую часть уравнения множественной регрессии.

Если сравнить коэффициенты парной и частной корреляции, то можно увидеть, что из-за низкой межфакторной зависимости коэффициенты парной корреляции дают корректные оценки тесноты связи:

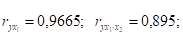
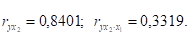
Итак, у обоих факторов теснота парной зависимости больше, чем теснота межфакторной связи. Следовательно, имеем слабую коллинеарность (взаимосвязь) факторов, поэтому x1 (кредитные вложения) и x2 (суммарный риск) должны быть включены в исследование.

Линейное уравнение множественной регрессии у от x1 и x2 имеет вид:

Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизированном масштабе:

Расчет коэффициентов выполним по формулам:

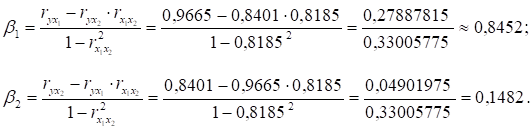
Получим уравнение:

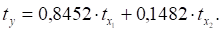
Для построения уравнения в естественной форме рассчитаем b1 и b2, используя формулы перехода от к bi:

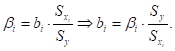
Для рассматриваемой задачи имеем:

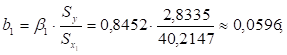
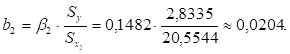
Значение b0 определим из соотношения.

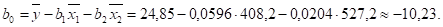
Итак, уравнение множественной регрессии имеет вид:

Значение b0 оценивает агрегированное влияние прочих (кроме учтенных в модели факторов x1 и x2) факторов на результат у.

Величины b1 и b2 указывают, что с увеличением х1 и х2 на единицу их значений результат увеличивается соответственно на 0,0596 и на 0,0204 млн. ден. ед. Полученные частные коэффициенты корреляции икоэффициенты одинаково подтверждают ранжирование факторов по силе их воздействия на результат:

и то есть сумма кредитных вложений x1 влияет на результат у сильнее, чем фактор суммарного риска x2.

Рассчитаем линейный коэффициент множественной корреляции с использованием и :

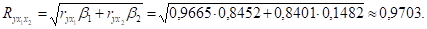
Оценку надежности уравнения регрессии и показателя тесноты связи дает F-критерий Фишера. Анализ выполним сравнением фактического и табличного (критического) значений F-критерия Фишера Fта6л и Fфакт, которые определяем из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

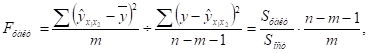
где n — число единиц совокупности, m — число факторов в уравнении регрессии.

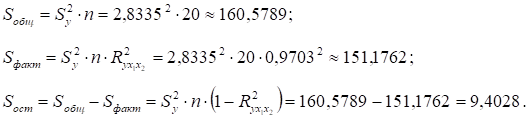
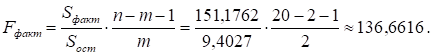
По таблицам значений F-критерия Фишера по уровню значимости = 0,05 и числу степеней свободы k1 = m = 2 и k2 = n — m — 1 = 17 находим Fтa6л = 3,59.

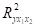
Так как Fфакт = 136,6616 > Fтa6л = 3,59, то гипотеза о статистической незначимости уравнения регрессии в целом и показателя тесноты связи отвергается. То есть уравнение регрессии и значениястатистически надежны и сформировались под систематическими воздействиями неслучайных причин.

Вероятность того, что допускаются ошибки при отклонении гипотезы Н0, не превышает 5%.

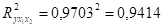
Нескорректированный коэффициент множественной регрессии оценивает долю вариации результата за счет представленных в уравнении факторов в общей вариации результата. Здесь эта доля составляет 94,14% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов х1 и х2.

Скорректированный коэффициент множественной детерминации.

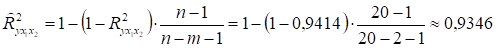
определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсии. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на высокую (порядка 94%) детерминированность результата у в модели с факторами х1 и х2.

Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора х1 в модель после того, как в нее включен фактор х2. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами х1 и х2:

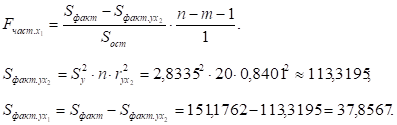
По таблицам значений F-критерия Фишера Fтa6л = F (0,05;1;17) = 4,45.

Так как.

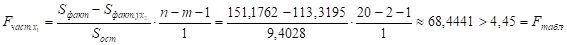
то включение фактора х1 после фактора х2 оказывается статистически значимым и оправданным. Таким образом, фактор х1 должен присутствовать в уравнении, в том числе в варианте, когда он дополнительно включается после фактора х2.

Поменяем порядок включения факторов в модель и рассмотрим варианты включения х2 после х1. Выполним расчет с использованием показателей тесноты связи и :

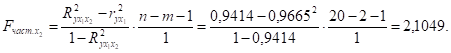
Так как приходим к выводу, что включение в модель фактора х2 после введения в нее фактора х1 оказалось бесполезным, влияние фактора х2 не является устойчивым и систематическим.

На основе частных F-критериев Фишера оценим значимость коэффициентов b1 и b2.

Вычислим t-критерии Стьюдента для коэффициентов регрессии линейного уравнения как квадратный корень из соответствующего частного F-критерия Фишера:

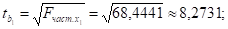
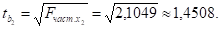
Табличные (критические) значения t-критерия Стьюдента зависят от уровня значимости, числа свободы k = n — m — 1 (n — объем совокупности, m — число факторов в уравнении). Таким образом, tкp = t (0,05; 20 — 2 — 1 = 17) = 2,1098.

Так как значение больше критического значения t-критерия Стьюдента tкp = 2,1098, то коэффициент регрессии b1 является статистически значимым, на него можно опираться в прогнозе.

Так как значение меньше критического значения t-критерия Стьюдента tкp = 2,1098, то величина b2 является статистически незначимой, ненадежной в силу того, что она формируется под воздействием случайных факторов.

Общий вывод состоит в том, что множественная модель с факторами х1 и х2 содержит неинформативный фактор x2. Если его исключить, то можно ограничиться уравнением парной регрессии:

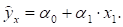
Коэффициент регрессии.

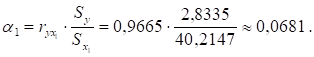
Тогда.

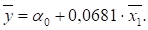
Из указанного уравнения.

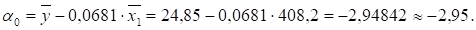
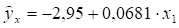
Итак, уравнение парной регрессии вида является окончательным, оно более простое, детерминированное и пригодно для прогноза и анализа.

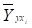
Средние частные коэффициенты эластичности показывают, на сколько процентов от значения своей средней изменяется результат при изменении фактора xi на 1% от своей средней и при фиксированном воздействии на у всех прочих факторов, включенных в уравнение регрессии. Для линейной зависимости.

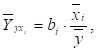
где bi — коэффициент регрессии при xi в уравнении регрессии. Таким образом,.

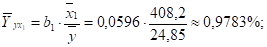
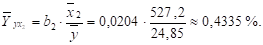
По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у фактора кредитных вложений x1, чем фактора суммарного риска х2: 0,9783% против 0,4335%.

Задание 3.

В начале планового периода продолжительностью в N лет имеется оборудование возраста t. Известны стоимость r (t) продукции, производимой в течение года с использованием этого оборудования; ежегодные расходы (t), связанные с эксплуатацией оборудования; его остаточная стоимость s; стоимость р нового оборудования (сюда же включены затраты, связанные с установкой, наладкой и запуском оборудования):

Требуется:

Пользуясь функциональными уравнениями, составить матрицу максимальных прибылей Fn (t) за N лет;

Сформировать по матрице максимальных прибылей оптимальные стратегии замены оборудования данных возрастов T и T1 лет в плановом периоде продолжительностью соответственно N и N1 лет.

Решение:

Для решения задания применим принцип оптимальности Р. Беллмана, Рассмотрим интервалы времени, то есть годы, планового периода от конца к началу. Обозначим функцию условно-оптимальных значений функции цели Fk (t) — максимальную прибыль, которая будет получена от использования оборудования возраста t лет за последние k лет планового периода (см. рисунок 3.1).

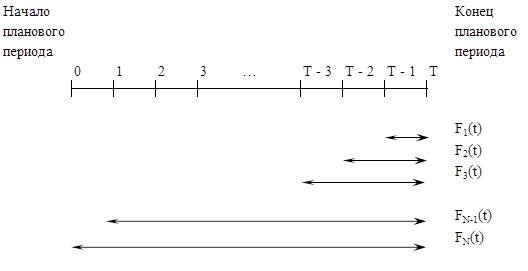
Рисунок 3.1.

Запишем функциональные уравнения для последнего года планового периода F1(t) и последних k лет планового периода Fk (t) при исходных числовых значениях задачи:

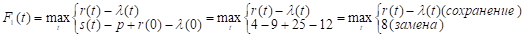
(1).

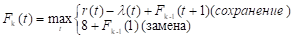
(2).

Пользуясь этими выражениями, будем последовательно вычислять значения максимальной прибыли Fk (t) и записывать их в таблицу 3.1. Первую строку получим, придавая параметру t в равенстве (1) значения 0, 1, 2, …, 10 и используя исходные данные. Например, при t = 0:

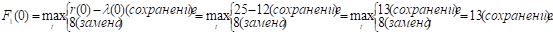
Аналогично расчет ведется до t = 4. Заметим, что если вдруг прибыль от нового оборудования равна прибыли от старого, то старое лучше сохранить еще на год.

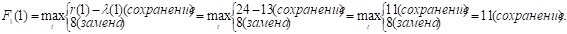
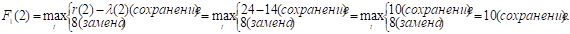
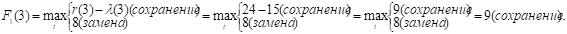
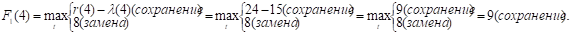
При t = 5:

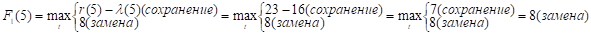
и т.д.

Из таблицы исходных данных видно, что r (t) — (t) с ростом t убывает. Поэтому при t > 4 оптимальной будет политика замены оборудования. Чтобы различать, в результате какой политики получается условно-оптимальное значение прибыли, будем эти значения разграничивать (до t = 4 включительно оптимальной является политика сохранения). Для заполнения второй строки таблицы 3.1 используем формулу (2) для k = 2:

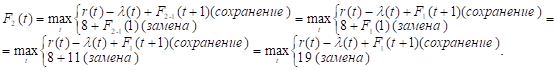
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F1(t+1) из первой строки таблицы, заполним вторую ее строку:

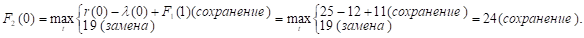
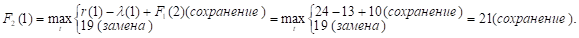
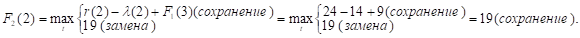
Прибыль от нового оборудования равна прибыли от старого, сохраняем его еще на год. При t = 3.

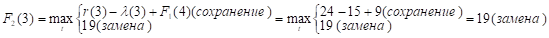
и т.д.

Так как r (t) — (t) с ростом t убывает, то до t = 2 включительно оптимальной будет политика сохранения оборудования, а при t > 2 — политика его замены. Для заполнения третьей строки таблицы используем формулу (2) для k = 3:

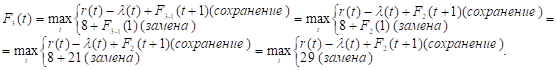
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F2(t+1) из второй строки таблицы, заполним ее третью строку:

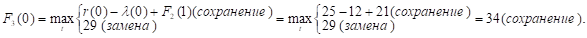
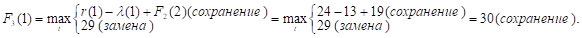
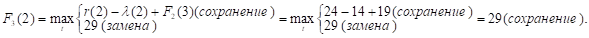
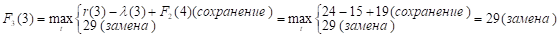
Так как r (t) — (t) с ростом t убывает, то до t = 2 включительно оптимальной будет политика сохранения оборудования (при t = 2 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 2 — политика замены оборудования. Для заполнения четвертой строки таблицы используем формулу (2) для k = 4:

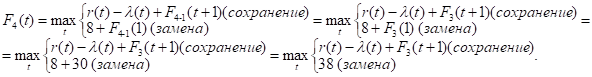
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F3(t+1) из третьей строки таблицы, заполним ее четвертую строку:

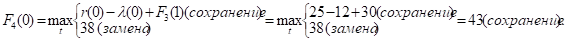
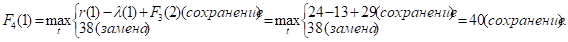
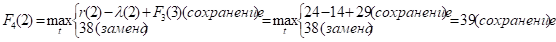
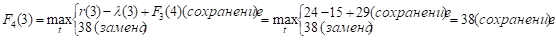
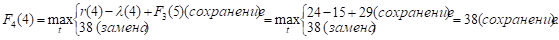
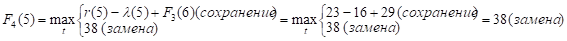
и т.д.

Как видно, до t = 4 включительно оптимальной будет политика сохранения оборудования (при t = 3 и t = 4 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 4 — политика его замены. Для заполнения пятой строки таблицы используем формулу (2) для k = 5:

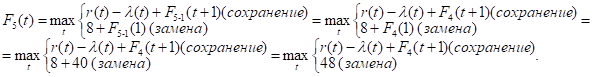
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F4(t+1) из четвертой строки таблицы, заполним пятую строку:

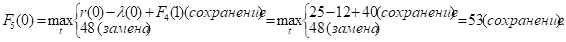
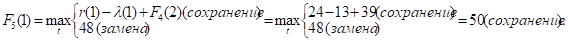
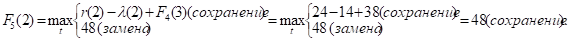
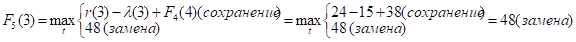
и т.д.

Как видно, до t = 2 включительно оптимальной будет политика сохранения оборудования (при t = 2 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 2 — политика замены оборудования. Для заполнения шестой строки таблицы используем формулу (2) для k = 6:

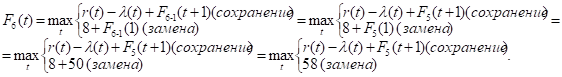
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F5(t+1) из пятой строки таблицы, заполним шестую строку:

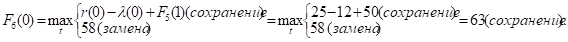
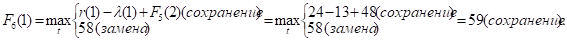
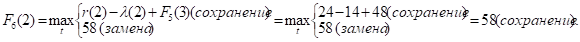
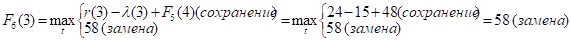
и т.д.

Как видно, до t = 2 включительно оптимальной будет политика сохранения оборудования (при t = 2 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 2 — политика его замены. Для заполнения седьмой строки таблицы используем формулу (2) для k = 7:

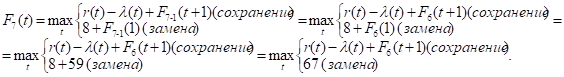
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F6(t+1) из шестой строки таблицы, заполним седьмую строку:

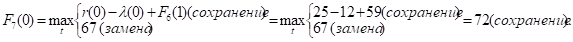
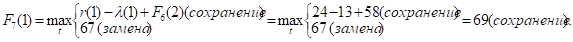
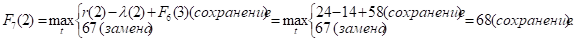
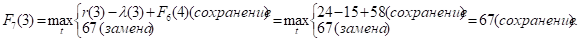
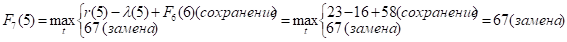
и т.д.

Как видно, до t = 4 включительно оптимальной будет политика сохранения оборудования (при t = 3 и t = 4 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 4 — политика замены оборудования.

Для заполнения восьмой строки таблицы используем формулу (2) для k = 8:

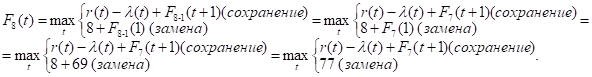
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F7(t+1) из седьмой строки таблицы, заполним восьмую строку:

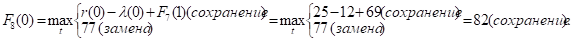
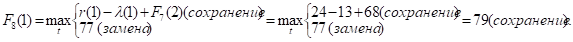
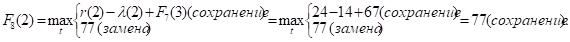
и т.д.

Как видно, до t = 2 включительно оптимальной будет политика сохранения оборудования (при t = 2 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 2 — политика его замены. Для заполнения девятой строки таблицы используем формулу (2) для k = 9.

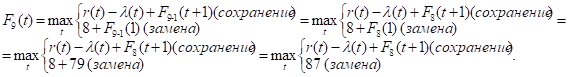
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F8(t+1) из восьмой строки таблицы, заполним девятую строку:

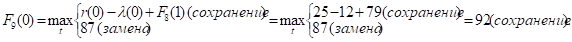
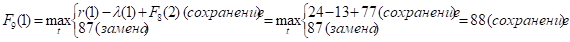
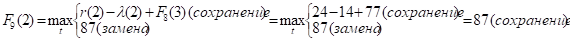
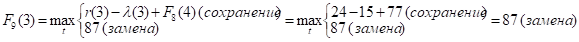
и т.д.

Как видно, до t = 2 включительно оптимальной будет политика сохранения оборудования, (при t = 2 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 2 — политика замены оборудования. Для заполнения десятой строки таблицы используем формулу (2) для k = 10:

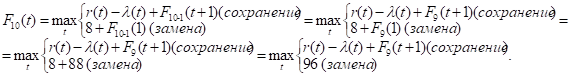
Придавая параметру t значения 0, 1, 2, …, 10 и используя исходные данные и значения F9(t+1) из девятой строки таблицы, заполним десятую строку:

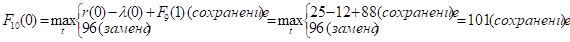
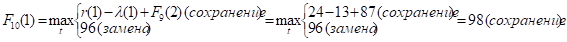
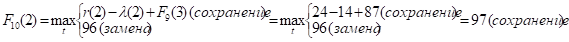
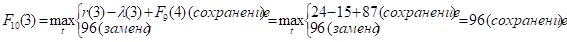
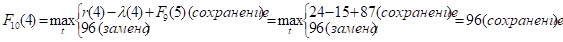
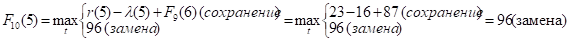
и т.д.

Как видно, до t = 4 включительно оптимальной будет политика сохранения оборудования (при t = 3 и t = 4 прибыль от нового оборудования равна прибыли от старого, его лучше сохранить еще на год), а при t > 4 — политика его замены. Итак, по окончании вычислений наша расчетная таблица 3.1 примет вид:

Таблица 3.1.

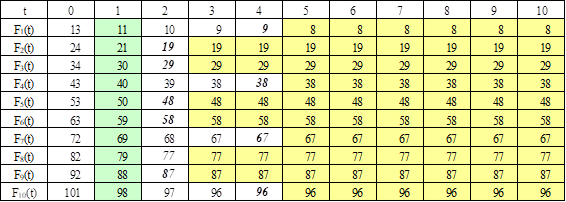
Пусть, например, в начале планового периода имелось оборудование возраста Т = 6 лет. Разработаем политику «замен» на десятилетний период, доставляющий максимальную прибыль. Информация для этого представлена в расчетной таблице 3.1. Максимальная прибыль, которую можно получить за N = 10 лет при условии, что в начале планового периода имелось оборудование возраста 6 лет, находится в таблице на пересечении столбца t = 6 строки F10(t). Она составляет 96 единиц.

Значение максимальной прибыли F10(6) = 96 записано в области «политики замены» (область «политики замены» обозначена в таблице цветной заливкой, соответственно область левее «залитых» ячеек ограничивает зону «политики сохранения»). Это значит, что для достижения в течение 10 лет максимальной прибыли в начале первого года оборудование надо заменить. В течение первого года новое оборудование постареет на год, то есть, заменив оборудование и проработав на нем 1 год, мы за 9 лет до конца планового периода будем иметь оборудование возраста 1 год. Из расчетной таблицы берем F9(1) = 88. Это значение располагается в области «политики сохранения», то есть во втором году планового периода надо сохранить оборудование возраста 1 год, и, проработав на нем год, за 8 лет до конца планового периода будем иметь оборудование возраста 2 года.

Значение F8(2) = 77 размещено в области сохранения. Работаем на оборудовании еще год. Теперь до конца планового периода осталось 7 лет, а возраст оборудования составляет 3 года. Находим F7(3) = 67. Это область сохранения. Работаем на оборудовании еще год. Его возраст становится равным 4 годам. До конца планового периода остается 6 лет. Определяем Fб (4) = 58. Это область замены. Заменяем оборудование на новое. Проработаем на нем в течение пятого года. До конца планового периода остается 5 лет. Имеем оборудование возрастом 1 год. Определяем F5(1) = 50. Это область сохранения. Работаем на оборудовании в течение следующего шестого года планового периода. Оно постареет на год. До конца планового периода остается 4 года. Продолжая подобные рассуждения, получим, что F4(2) = 39 (область сохранения), F3(3) = 29 (область замены), F2(1) = 21 (область сохранения), F1(2) = 10 (также область сохранения). Разработанную политику изобразим следующей цепочкой:

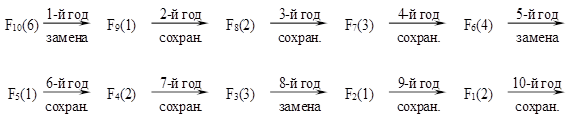
Из составленной расчетной таблицы можно найти оптимальную стратегию замены оборудования с любым начальным состоянием от 0 до 10 лет и на любой плановый период, не превосходящий 10 лет. Например, найдем «политику замен» на шестилетний период (N1 = 6), приносящий максимальную прибыль, если в начале имелось оборудование возраста T1 = 4 года:

Максимальная прибыль, которую можно получить за N = 6 лет при условии, что в начале планового периода имелось оборудование возраста 4 года, находится в таблице на пересечении столбца t = 4 и строки FN (t) = F6(4). Она составляет 58 единиц.

Значение максимальной прибыли F6(4) = 58 находится в области «политики замены». Это значит, что для достижения в течение 6 лет максимальной прибыли оборудование надо заменить. В течение первого года замененное оборудование постареет на год, то есть, проработав на нем 1 год, мы за 5 лет до конца планового периода будем иметь оборудование возраста 1 год. Из расчетной таблицы берем F5(1) = 50. Это значение располагается в области «политики сохранения», то есть во втором году планового периода надо сохранить оборудование возраста 1 год, и, проработав на нем год, за 4 года до конца планового периода будем иметь оборудование возраста 1 + 1 = 2 года. Значение F4(2) = 39 размещено в области сохранения. Работаем на оборудовании в третий год планового периода. Теперь до конца планового периода осталось 3 года, а возраст оборудования составляет 2 + 1 = 3 года. Находим F3(3) = 29. Это область «политики замены», поэтому оборудование меняем на новое. Работаем на нем в течение четвертого года планового периода и получаем на выходе оборудование возрастом 1 год. До конца планового периода остается 2 года. F2(1) = 21. Область сохранения, продолжаем работать пятый год планового периода и получаем на выходе оборудование возрастом 2 года. До конца планового периода остается 1 год. F1(2) = 10 (область сохранения). Разработанную политику можно отобразить следующей цепочкой:

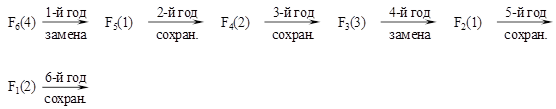
Задание 4.

Предположим, что спрос составляет = 3 200 единиц товара в год, которые поставляются равномерно и непрерывно со склада. Организационные издержки составляют К = 80 у.е. за одну партию, а издержки хранения равны s = 1,3 у.е. в расчете на одну единицу товара в год. Запасы на складе пополняются с некоторой производственной линии, которая работает со скоростью = 4 800 единиц товара в год. Производственная линия начинает действовать, как только уровень запасов на складе становится равным нулю, и продолжает работу до тех пор, пока не будет произведено q единиц товара.

Требуется:

Найти размер партии, который минимизирует все затраты;

Минимальные среднегодовые издержки на размещение заказов и содержание запасов;

Вычислить время, в течение которого продолжается поставка;

Вычислить продолжительность цикла;

Найти максимальный и средний уровень запасов при условии, что размер поставки оптимален;

Нарисовать график изменения запасов;

Определить, на сколько % изменятся (увеличатся или уменьшатся) оптимальные среднегодовые издержки на размещение заказов и хранение запасов при увеличении (уменьшении) оптимальной партии поставки на = 25%;

Определить, на сколько % изменятся (увеличатся или уменьшатся) оптимальные среднегодовые издержки на размещение заказов и хранение запасов с изменением оптимальной партии поставки при увеличении (уменьшении) издержек хранения единицы продукции на = 30% и накладных расходов, связанных с размещением заказа и поставкой партии на = 35%;

Определить, на сколько % изменятся (увеличатся или уменьшатся) оптимальные среднегодовые издержки на размещение заказов и хранение запасов без изменения оптимальной партии поставки при увеличении (уменьшении) издержек хранения единицы продукции на = 30% и накладных расходов, связанных с размещением заказа и поставкой партии на = 35%.

Решение:

Товар поступает на склад с производственной линии с постоянной интенсивностью = 4 800 ед. в год. На склад товар поступает партиями размером q ед. Пополнение склада происходит в каждом цикле за время 1, а потребление — за = 1 + + 2. Абсолютная интенсивность увеличения запасов определяется разностью —, где = 3 200 ед. в год — интенсивность расходования запасов. Максимальный уровень запасов за время 1 возрастет на величину р = (-). 1. Так как 1 = q /, величина среднего запаса равна (-). q / 2. Учитывая, что запас р, накопленный в интервале 1, полностью расходуется за время 2, имеем р =. 2. Тогда получим. 2 = (-). q / .

Следовательно,.

2 = (-). q / .

Поэтому.

= 1 + 2 = q / + (-). q / = q / .

Определим суммарные затраты, связанные с организацией заказов и содержанием запасов, приходящиеся на один цикл:

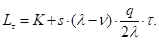
Разделив это выражение на длину цикла = q /, получим величину издержек в единицу времени:

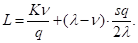
Оптимальный объем партии поставки q*, минимизирующий общие затраты, вычислим, приравнивая к нулю производную:

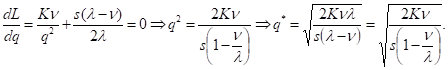
Тогда оптимальный интервал возобновления заказов:

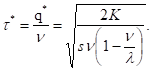
Найдем оптимальные издержки в единицу времени:

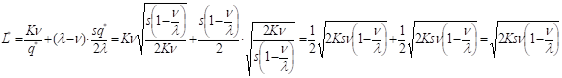
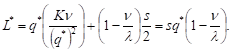
Размер партии, который минимизирует все затраты:

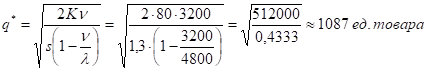
Минимальные среднегодовые издержки на размещение заказов и содержание запасов составят:

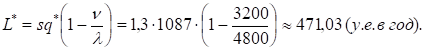
Продолжительность поставки:

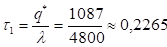
года,.

что составляет 0,2265. 365 83 дня.

Продолжительность цикла.

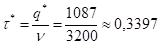
года, что составляет 0,3397. 365 124 дня.

Максимальный уровень запасов.

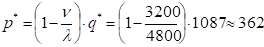
ед. товара.

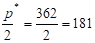
Средний уровень запасов ед. товара.

График изменения запасов изображен на рисунке. Заметим, что масштаб выбирается в зависимости от того, как соотносятся полученные значения * и 1.

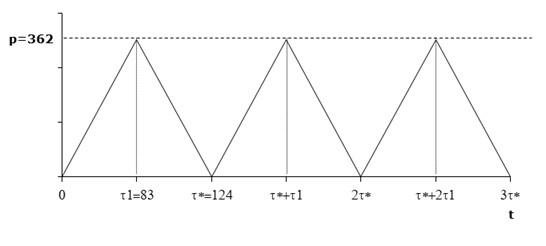
Заметим, что.

Тогда в случае увеличения оптимальной партии поставки на = 25%,.

получимСледовательно,.

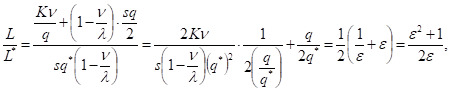
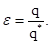
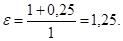
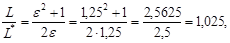
что влечет увеличение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 2,5% (1,025 — 1 = 0,025).

В случае уменьшения оптимальной партии поставки на = 25%,.

получимСледовательно,.

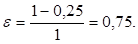
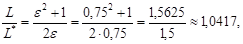
что влечет увеличение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 4,17% (1,0417 — 1 = 0,0417).

Заметим, что.

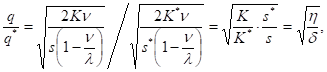
Тогда в случае увеличения издержек хранения единицы продукции на = 30% и увеличения накладных расходов, связанных с размещением заказа и поставкой партии на = 35%, получим Следовательно,.

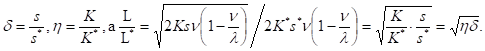
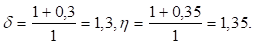
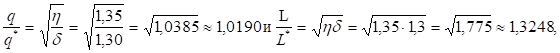
что влечет увеличение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 32,48% (1,3248 — 1 = 0,3248), при соответствующем увеличении оптимальной партии поставки на 1,9% (1,019 — 1 = 0,019).

В случае уменьшения издержек хранения единицы продукции на = 30% и уменьшения накладных расходов, связанных с размещением заказа и поставкой партии на = 35%, получим Следовательно,.

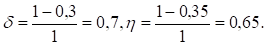
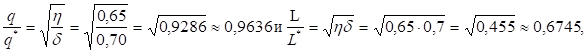
что влечет уменьшение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 32,55% (0,6745 — 1 = -0,3255), при соответствующем уменьшении оптимальной партии поставки на 3,64% (0,9636 — 1 = -0,0364).

Заметим, что.

.

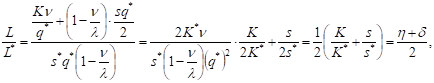
Тогда в случае увеличения издержек хранения единицы продукции на = 30% и увеличения накладных расходов, связанных с размещением заказа и поставкой партии на = 35% получим Следовательно,.

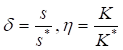
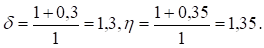
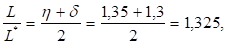
что влечет увеличение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 32,5% (1,325 — 1 = 0,325) без изменения оптимальной партии поставки.

Тогда в случае уменьшения издержек хранения единицы продукции на = = 30% и уменьшения накладных расходов, связанных с размещением заказа и поставкой партии на = 35% получим Следовательно,.

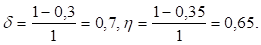
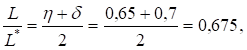
что влечет уменьшение оптимальных среднегодовых издержек на размещение заказов и хранение запасов на 32,5% (0,675 — 1 = -0,325) без изменения оптимальной партии поставки.

Задание 5.

Предприятие, А независимо от выполнения плана в предыдущем месяце в следующем план перевыполнит с вероятностью р = 0,25, не выполнит с вероятностью q = 0,2 и выполнит план на 100% с вероятностью r = 1 — р — q = 1 — 0,25 — 0,2 = 0,55. Предприятие В план перевыполнит с вероятностью р + = 0,25 + 0,1 = 0,35, р = 0,25, р — = 0,25 — 0,1 = 0,15 соответственно, если в предыдущем месяце план перевыполнен, выполнен на 100% и не выполнен. Вероятности невыполнения плана при этом будут равны q — = 0,2 — 0,1 = 0,1, q = 0,2, q + = 0,2 + 0,1 = 0,3. Найти финальные вероятности для, А и В и исследовать их.

Решение:

Множество состояний предприятий, А и В следующее: 1 — план перевыполнен, 2 — выполнен на 100%, 3 — не выполнен. Для предприятий, А и В переходные матрицы имеют вид то есть.

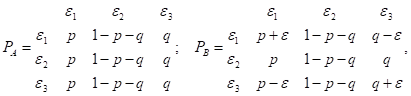
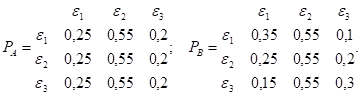
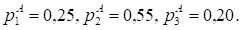
Так как для предприятия, А переходная матрица не зависит от номера строки, то матрица финальных вероятностей совпадает с матрицей РА. Тогда Чтобы найти финальные вероятности для предприятия В, необходимо решить следующую систему линейных уравнений:

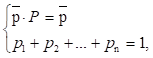
где Р — переходная матрица, = (р, р2, …, рn) — вектор-строка, n — количество состояний.

Тогда.

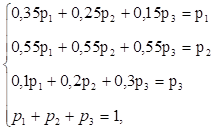
где p1, p2, p3 — искомые вероятности.

Из второго и четвертого уравнения системы:

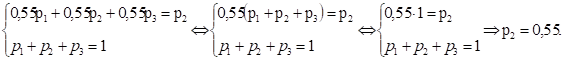
Из третьего и четвертого уравнения системы:

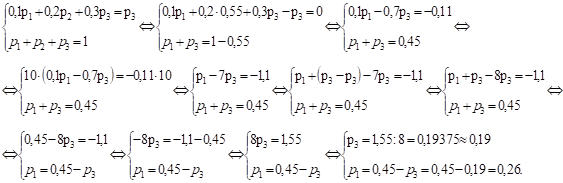
Итак,.

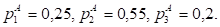
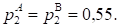
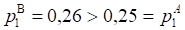
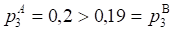
Выводы: в результате произведенных вычислений можно говорить, что у обоих предприятий, А и В вероятности выполнения плана совпадают (так, вероятность выполнения плана на 100% у обоих компаний Вероятность перевыполнения плана у предприятия В выше, чем у предприятия, А (). Вероятность невыполнения плана предприятием, А превышает такую же возможность у предприятия В ().

• 1. Эконометрика: учебник / ИИ. Елисеева, С. В. Курышева Т.В. Костеева и др.; под ред. И. И. Елисеевой. 2-е изд., перераб. и доп. — М: Финансы и статистика, 2007. — 576 с.: ил.
• 2. Практикум по эконометрике: Учеб. пособие / И. И. Елисеева, С. В. Курышева, Н. М. Гордеенко и др.; под ред. И. И. Елисеевой — М: Финансы и статистика, 2002. — 192 с.: ил.
• 3. Сборник задач по эконометрике: Учебное пособие для студентов экономических вузов / Сост. Е. Ю. Дорохина, Л. Ф. Преснякова, Н. П. Тихомиров. — М.: Издательство «Экзамен», 2003. — 224 с.
• 4. Эконометрика: Учебное пособие в схемах и таблицах / Н. М. Гордеева, Л. Н. Демидова, Л. М. Клизогуб, С. А. Орехов, Н. А. Сердюкова, С. Т. Швецова; под ред. д-ра экон. наук, проф. С. А. Орехова — М: Эксмо, 2008. — 224 с. — (Экономика — наглядно и просто).