Подготовка и проведение активного эксперимента при исследовании статических и динамических характеристик

Исследование характеристик объекта в большинстве случаев производится в разомкнутом контуре. При этом регулятор отключают и переходят на ручное управление, возмущающие воздействия стабилизируются. Перед проведением эксперимента необходимо установить диапазон изменения входных и выходных сигналов и ориентировочное число точек статической характеристики. Для получения статических характеристик сначала устанавливают минимальные (или максимальные) значения переменных. Убедившись, что входные и выходные сигналы не изменяются во времени, заносят их значения в таблицу и производят изменение входного сигнала.

После окончания переходного процесса (выходной сигнал становится практически постоянным) полученные значения входа и выхода заносят в таблицу и т. д. При наличии нескольких входов эксперимент повторяется при различных значениях «свободных» переменных.

Как известно, параметры линейной модели существенно зависят от рабочего режима. Поэтому исследования динамики проводят для всех основных рабочих режимов. перед подачей испытательного сигнала объект выводится на рабочий режим и стабилизируются все возмущения на время снятия переходной кривой, иными словами, устанавливаются «нулевые» начальные условия.

х = хн = const, у = ун = const.

Убедившись, что нулевые начальные условия установлены, изменяют входной сигнал, одновременно на диаграмме отмечают момент нанесения воздействия и регистрируют изменение входного сигнала до нового установившегося значения.

Простейшим испытательным воздействием является единичное скачкообразное воздействие х (t) = 1(t). Реакция звена (или системы) h (t) на единичное скачкообразное воздействие при нулевых начальных условиях называется переходной кривой.

В реальном эксперименте (рис. 1) амплитуда входного сигнала отлична от единицы, что в силу линейности модели приводит к пропорциональному изменению выходного сигнала. В дальнейшем это обстоятельство будет учитываться умножением h (t) на х. Если длительные отклонения выходного сигнала недопустимы, то на вход объекта подаются импульсные воздействия, например, как на рис. 2.

Для более точного определения переходной кривой эксперимент повторяют несколько раз, изменяя знак входного воздействия.

Следует обратить внимание на своевременность регистрации момента изменения x (t), так как от этого зависит точность определения запаздывания (рис. 1), а также на тщательность установки начальных условий. В противном случае могут возникнуть большие ошибки при определении параметров модели.

Амплитуда воздействия выбирается такой, чтобы изменение у было достаточно велико, но в то же время не превышало допустимых значений и не нарушалось условие линейности. Обычно значение х = А выбирается по статической характеристике или подбирается экспериментально путем пробных воздействий.

Обзор методов идентификации передаточных функций по переходной характеристике.

Идентификация W (s) по переходной характеристике является одним из простейших методов. При идентификации передаточной функции.

.

неизвестным помимо коэффициентов аi, bi, K, является порядок W (s), т. е. значения n и m. Иногда порядок W (s) определяют исходя из физических соображений или имеющегося опыта, в противном случае определяют несколько моделей различного порядка.

Параметры моделей выбирают из условий близости выходных сигналов объекту уоб и модели ум. Близость объекта и модели можно оценить по следующим критериям:

I1 = ,.

где t — интервал разбиения кривой разгона; N — число точек разбиения.

I2 = max{|yоб (i. t) — yм (i. t)| / yобmax}.

В качестве рабочей выбирается модель, соответствующая минимуму критерия близости.

Для удобства расчетов переходная кривая (рис. 1) перестраивается в новых осях координат (переход к отклонениям).

Коэффициент усиления К определяют по формуле:

К = ууст / х, запаздывание — непосредственно по кривой разгона (рис. 3).

Нормированные разгонные характеристики (в отклонениях) Для более точного определения оно находится как среднее арифметическое нескольких экспериментов.

Остальные параметры передаточной функции можно найти несколькими методами. Рассмотрим некоторые из них.

Методы первого порядка.

Передаточная функция и переходная кривая модели.

Wм (s) = ,.

h (t) = K (1 —).1(t).

Определение параметров модели по методу касательной Постоянная времени Т определяется как длина подкасательной, проведенной к кривой в точке t = (рис. 3, а) или в точке перегиба t = tw (рис. 3, б).

В этом случае вводится дополнительное запаздывание д (рис. 3б), а модель характеризуется эквивалентным запаздыванием о = + д.

Описанный метод является довольно грубым, его можно использовать для предварительной оценки свойств объекта.

Интерполяционный метод Орманса.

Пусть основное запаздывание уже выделено (рис. 4), начало координат смещено в точку t =. Потребуем, чтобы переходная кривая модели проходила через точки, А и В.

Выделение характерных точек на кривой разгона Подставляя координаты (tA, yA) и (tB, yB) точек, А и В и = д в формулу (27), для y (t) получим систему из двух уравнений:

yА = K (1 —) х,.

yВ = K (1 —) х.

Решение системы (28) относительно д и Т имеет вид:

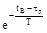
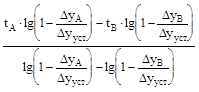
д = ,.

Т = - .

Если принять yА = 0,33. yуст, а yВ = 0,7. yуст, то выражения (29) значительно упрощаются:

д = 0,5.(3.tА — tВ), Т = 1,25.(tВ — tА).

Для проверки точности модели ординаты экспериментальной кривой в точках.

t1 = 0,8.Т + д, t2 = 2. Т + д.

сравниваются с соответствующими ординатами переходной кривой модели y1 = 0,33. yуст, y2 = 0,865. yуст. Погрешность не должна превышать (0,02 + 0,03. yуст).

Модель второго порядка.

Передаточная функция и переходная характеристика модели имеют вид.

Wм (s) = ,.

h (t) = K.

Метод Олденбурга и Сарториуса Рассмотрим метод Олденбурга и Сарториуса [1, 4]. Значения К определяются по формуле (8), — по переходной кривой (рис. 4). Метод основан на соотношениях, связывающих характерные точки h (t) с постоянными времени Т1 и Т2 модели (31).

Для определения Т1 и Т2 в точке перегиба к переходной кривой (рис. 4) проводится касательная и определяются константы ТС и ТА.

По определению в точке перегиба вторая производная у (2)(tw) равна нулю:

х.h (2)(tw) = 0.

Используя константы ТС и ТА и рис. 4, запишем выражения для первой производной h (t) в точке перегиба:

х. h (1)(tw) = yуст / ТА = tg ,.

х. h (1)(tw) = (yуст — y (tw)) / ТC = tg .

Определив из (31) выражения h (tw), h (1)(tw) и h (2)(tw), подставив их в (32) и (33), исключив (tw —), получим систему.

.

1 + 2 = ,.

где 1 = Т1 / ТА, 2 = Т2 / ТА, = ТС / ТА.

Система (34) является исходной для определения Т1 и Т2. Ее решение удобно производить графически помощью номограммы (рис. 8).

Первое уравнение системы (34) определяет так называемую L_кривую, второе — прямую, отсекающую по осям координат отрезки длиной (рис. 8).

1 + 2 =.

и L-кривой определяют значения.

1 = Т1 / ТА и 2 = Т2 / ТА.

Порядок определения постоянных времени Т1 и Т2 следующий:

• 1) проводится касательная к у (t) в точке перегиба;
• 2) определяются константы ТС и ТА и значение = ТС / ТА;
• 3) через точки с координатами (0,) и (, 0) проводится прямая (рис. 8) и по координатам точек пересечения определяются Т1 и Т2.

Отметим, что для модели (31) значение лежит в пределах 0,73 1. При = 0,73 прямая касается L-кривой и Т1 = Т2 = 0,365. ТА. Если < 0,73, то модели вида (31) не существует. В этом случае необходимо использовать модель другого вида.