Методы. 
Приближенные методы решения обыкновенных дифференциальных уравнений

В первую очередь рассмотрим функциональные методы решения простейших дифференциальных уравнений, применение которых дает решение в виде функции, представленной аналитически.

Интегрирование дифференциальных уравнений с помощью степенных рядов.

Рассмотрим этот метод в общем случае для дифференциального уравнения n-го порядка при начальных условиях:

,…,. (2).

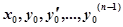
Предположим, что правая часть уравнения (1) является аналитической функцией в начальной точке, т. е. в некоторой окрестности этой точки разлагается в степенной ряд вида:

.

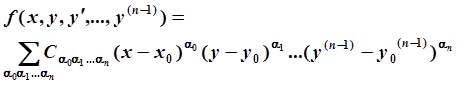
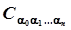
где — целые неотрицательные числа и — некоторые постоянные коэффициенты.

Тогда интеграл уравнения (1), отвечающий начальным условиям (2), является аналитическим в точке и, пользуясь рядом Тейлора, можно положить.

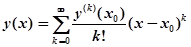
(3).

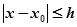
при .

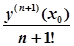
Первые n+1 коэффициентов ряда (3) определяются непосредственно из начальных условий (2) и дифференциального уравнения (1). Для нахождения следующего (n+2)-го коэффициента продифференцируем уравнение (1) по правилу дифференцирования сложной функции. В результате получим.

.

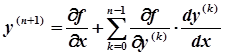
где для удобства принято .

Отсюда.

.

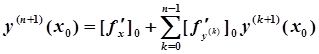
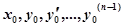
где значок «0» означает, что значения соответствующих производных берутся в точке (). Повторяя этот прием шаг за шагом, можно найти и дальнейшие производные, ,…

Пример: Написать несколько членов разложения в степенной ряд решения уравнения.

(4).

удовлетворяющего начальным условиям; .

Решение: Полагаем.

.

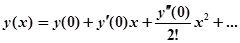
где и .

Из уравнения (4) получаем.

. (5).

Отсюда. Дифференцируя последовательно уравнение (5), будем иметь.

;

;

;

Из этих равенств вытекает, что.

;

;

.

Следовательно,.

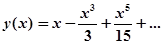
Написать общий член ряда не представляет больших затруднений.

Метод разложения решения дифференциального уравнения в степенные ряды часто используется как элемент более практичных методов приближенного интегрирования дифференциальных уравнений. В частности, для некоторых численных методов интегрирования дифференциальных уравнений требуется определить значение искомых функций в нескольких точках. Эти значения при соблюдении известных условий гладкости данного уравнения могут быть с любой степенью точности подсчитаны с помощью степенных рядов.

Метод Пикара (последовательных приближений).

Этот метод позволяет получить приближенное решение дифференциального уравнения в виде функции, представленной аналитически. Метод Пикара возник в связи с доказательством теоремы существования и единственности решения уравнения и является, по сути, одним из применений принципа сжимающих отображений.

Пусть в условиях теоремы существования требуется найти решение уравнения с начальным условием. Проинтегрируем обе части уравнения от до :

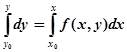
или.

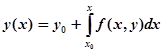
. (1).

Очевидно, решение этого интегрального уравнения будет удовлетворять дифференциальному уравнению и начальному условию. Действительно, при получим:

.

Вместе с тем интегральное уравнение (1) позволяет применить метод последовательных приближений. Положим и получим из (1) первое приближение:

.

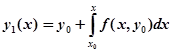
Интеграл в правой части содержит только переменную; после нахождения этого интеграла будет получено аналитическое выражения приближения как функции переменной. Заменим теперь в уравнении (1) у найденным значением и получим второе приближение:

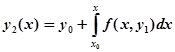
и т.д. В общем случае итерационная формула имеет вид:

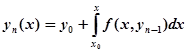
(n=1, 2,…). (2).

Циклическое применение этой формулы дает последовательность функций, ,…, ,…

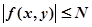
Так как функция непрерывна в области, то она ограничена в некоторой области, содержащей точку, т. е. .

Применяя к уравнению (2) в условиях теоремы существования принцип сжимающих отображений, нетрудно показать, что последовательность (3) сходится (имеется в виду сходимость по метрике.

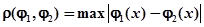
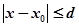
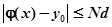
в пространстве непрерывных функций, определенных на сегменте, таких, что). Ее предел является решением интегрального уравнения (2), а следовательно, и дифференциального уравнения с начальными условиями. Это означает, что k-й член последовательности (3) является приближением к точному решению уравнения с определенной степенью точности.

Оценка погрешности k-го приближения дается формулой:

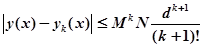
(5).

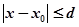
где — константа Липшица, — верхняя грань модуля функции из неравенства (4), а величина для определения окрестности вычисляется по формуле.

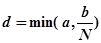
. (6).

Геометрически последовательные приближения представляют собой кривые (n=1, 2, …), проходящие через общую точку .

Пример: Методом последовательных приближений найти приближенное решение дифференциального уравнения, удовлетворяющее начальному условию .

Запишем для данного случая формулу вида (2):

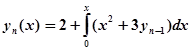
(n=1, 2,…).

Начальным приближением будем считать. Имеем:

.

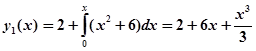
Далее получаем:

.

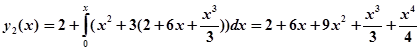
Аналогично:

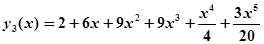
и т.д.

Оценим погрешность третьего приближения. Для определения области, заданной как.

.

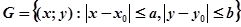
примем, например,,. В прямоугольнике функция определена и непрерывна, причем:

.

.

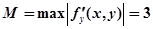
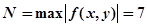
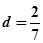
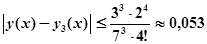
По формуле (6) находим. Используя оценочную формулу (5), получаем: .

Далее мы рассмотрим некоторые численные методы решения обыкновенных дифференциальных уравнений, дающие приближенное решение в виде таблицы.

Метод Эйлера.

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение с начальным условием. Выбрав достаточно малый шаг, построим, начиная с точки, систему равностоящих точек (i=0, 1, 2,…). Вместо искомой интегральной кривой на отрезке рассмотрим отрезок касательной к ней в точке (обозначим ее) с уравнением.

.

При из уравнения касательной получаем:, откуда видно, что приращение значения функции на первом шаге имеет вид: .

Аналогично, проводя касательную к некоторой интегральной кривой семейства в точке, получим:

.

что при дает.

.

т.е. получается из добавлением приращения.

.

Таким образом, получение таблицы значений искомой функции по методу Эйлера заключается в циклическом применении пары формул:

.

k=0, 1, 2,…

Метод Эйлера обладает малой точностью, к тому же погрешность каждого нового шага, вообще говоря, систематически возрастает. Наиболее приемлемым для практики методом оценки точности является в данном случае способ двойного счета — с шагом h и с шагом h/2. Совпадение десятичных знаков в полученных двумя способами результатах дает естественные основания считать их верными.

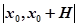
Если правая часть уравнения непрерывна, то последовательность ломаных Эйлера при на достаточно малом отрезке равномерно стремиться к искомой интегральной кривой .

Пример: Применяя метод Эйлера, составить на отрезке [0, 1] таблицу значений интеграла дифференциального уравнения.

.

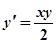
удовлетворяющего начальному условию, выбрав шаг h=0,1.

Результаты вычислений приведены в таблице. Для сравнения в последнем столбце помещены значения точного решения.

.

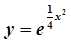
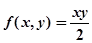Точное значение.
0 1 2 3 4 5 6 7 8 9 10	0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	1 1 1,005 1,0151 1,0303 1,0509 1,0772 1,1095 1,1483 1,1942 1,2479	0 0,05 0,1005 0,1523 0,2067 0,2627 0,3232 0,3883 0,4593 0,5374	0 0,005 0,0101 0,0152 0,0206 0,0263 0,0323 0,0388 0,0459 0,0537	1 1,0025 1,0100 1,0227 1,0408 1,0645 1,0942 1,1303 1,1735 1,2244 1,2840

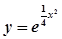
Из приведенной таблицы видно, что абсолютная погрешность значения составляет. Отсюда относительная погрешность примерно равна 3%.

Модификации метода Эйлера (метод Эйлера — Коши).

Существуют различные уточнения метода Эйлера, повышающие его точность. Модификации метода обычно направлены на то, чтобы более точно определить направление перехода из точки в точку .

Рассмотрим снова дифференциальное уравнение с начальным условием .

Выбрав шаг h, положим.

(i=0, 1, 2,…).

Согласно методу Эйлера последовательные значения искомого решения вычисляются по приближенной формуле.

.

где. Более точным является усовершенствованный метод ломаных, при котором сначала вычисляют промежуточные значения.

;

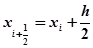
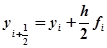
и находят значение направления поля интегральных кривых в средней точке, т. е.

.

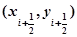
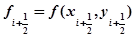
а затем полагают.

.

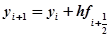
Другой модификацией метода Эйлера является усовершенствованный метод Эйлера — Коши, при котором сначала определяется «грубое приближение» решения.

.

исходя из которого находится направление поля интегральных кривых.

.

Затем приближенно полагают.

.

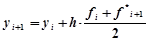
Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке (xi, yi) и во вспомогательной точке (xi+1, y*i+1), а в качестве окончательного берем среднее этих направлений.

Пример: Первым и вторым усовершенствованными методами Эйлера проинтегрировать уравнение.

.

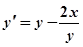
на отрезке [0,1].

Примем шаг h=0,2 и .

Приближенные значения искомого решения, определенные с помощью усовершенствованного метода ломаных, помещены в таблице 1.

В таблице 2 приведены результаты вычислений интеграла усовершенствованным методом Эйлера — Коши, причем шаг сохранен прежний h=0,2.

Таблица 1.

0 1 2 3 4 5	0 0,2 0,4 0,6 0,8 1,0	1 1,1836 1,3426 1,4850 1,6152 1,7362	0,1 0,0846 0,0747 0,0677 0,0625	0,1 0,3 0,5 0,7 0,9	1,1 1,2682 1,4173 1,5527 1,6777	0,1836 0,1590 0,1424 0,1302 0,1210

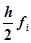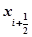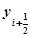
Для сравнения приводим точное решение, откуда …

Таблица 2.

0 1 2 3 4 5	0 0,2 0,4 0,6 0,8 1,0	1 1,1867 1,3484 1,4938 1,6279 1,7542	0,1 0,0850 0,0755 0,0690 0,0645	0,2 0,4 0,6 0,8 1,0	1,2 1,3566 1,4993 1,618 1,7569	0,0867 0,0767 0,0699 0,0651 0,0618	0,1867 0,1617 0,1454 0,1341 0,1263

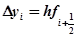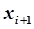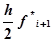
Метод Эйлера и его модификации являются простейшими представителями конечно-разностных методов (шаговых методов) для приближенного решения обыкновенных дифференциальных уравнений вида (k=1, 2,…, n) при заданных начальных условиях (k=1, 2,…, n).

При применении конечно-разностного метода искомое решение yk=yk (x) (k=1, 2,…, n) последовательно строится на системе точек (узлов) xi=x0+ih (I=0, 1, 2,…), где h — выбранный шаг. Процесс вычислений расчленяется на однообразно повторяющиеся циклы, каждый из которых обеспечивает переход от значения yk (xi) к значению yk (xi+1), начиная с начального y (0)k. Поэтому схема вычислений, вообще говоря, легко программируется и удобна для реализации на ЭВМ.

Метод Рунге-Кутта Метод Эйлера и метод Эйлера-Коши относятся к семейству методов Рунге-Кутта, имеющих следующий вид. Фиксируем некоторые числа:

последовательно вычисляем:

k1(h)=hf (x, y),.

k2(h)=hf (x+2h, y+21k1(h)),.

kq (h)=hf (x+qh, y+q1k1(h)+…+qq-1kq-1(h)).

и полагаем:

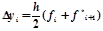
. (1).

Рассмотрим вопрос о выборе параметров i, pi, ij. Обозначим.

(h)=y (x+h)-z (h).

Будем предполагать, что.

(0)='(0)=…=(s)(0)=0.

при любых функциях f (x, y), а (s+1)(0)0 для некоторой функции f (x, y). По формуле Тейлора справедливо равенство.

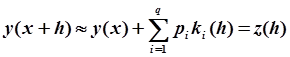
(2).

где 01. Величина (h) называется погрешностью метода на шаге, а s — порядком погрешности метода.

При q=1 будем иметь:

• (h)=y (x+h)-y (x)-p1hf (x, y),
• (0)=0,

'(0)=(y'(x+h)-p1f (x, y))h=0=f (x, y)(1-p1),.

«(h)=y"(x+h).

Ясно, что равенство '(0)=0 выполняется для любых функций f (x, y) лишь при условии, что р1=1. Легко видеть, что при этом значении р1 из формулы (1) получается формула.

yk=hf (xk, yk),.

yk+1=yk+yk, k=0, 1, 2,…,.

т.е. в этом случае мы получаем метод Эйлера. Для погрешности этого метода на шаге согласно (2) будем иметь:

.

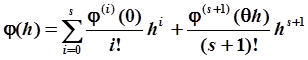
Рассмотрим случай q=2, тогда.

(h)=y (x+h)-y (x)-p1hf (x, y)-p2hf (x*, y*),.

где.

x*=x+2h, y*=y+21hf (x, y).

Согласно исходному дифференциальному уравнению.

y=f, y"=fx+fyf, y'''=fxx+2fxyf+fyyf2+fyy". (3).

(Здесь для краткости через y и f обозначены y (x) и f (x, y) соответственно.).

Вычисляя производные функции (h) и подставляя в выражения для (h), '(h) и «(h) значение h=0, получим (с учетом соотношений (3)):

(0)=0,.

'(0)=(1-p1-p2)f,.

«(0)=(1−2p22)fx+(1−2p221)fyf.

Хорошо видно, что требование.

(0)='(0)="(0)=0.

будет выполняться для всех f (x, y) лишь в том случае, если одновременно будут справедливы следующие три равенства относительно четырех параметров:

• 1-p1-p2=0,
• 1−2p22=0, (4)
• 1−2p221=0.

Произвольно задавая значение одного из параметров, и определяя значения остальных из системы (4), мы будем получать различные методы Рунге-Кутта с порядком погрешности s=2. Например, при р1= из (4) получаем: р2=, 2=1, 21=1. Для этих значений параметров формула (1) принимает вид:

.

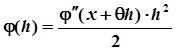
(Здесь yi+1 записано вместо y (x+h), yi — вместо y (x), а через y*i+1 обозначено выражение yi+hf (xi, yi).) Таким образом, в рассматриваемом случае мы приходим к расчетным формулам.

y*i+1=yi+hfi, f*i+1=f (xi+1, y*i+1,.

.

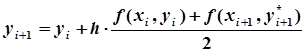
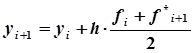
соответствующим методу Эйлера-Коши. Из (2) следует, что при этом главная часть погрешности на шаге есть, т. е. пропорциональна третьей степени шага h.

В вычислительной практике наиболее часто используется метод Рунге-Кутта с q=4 и s=4.

Приведем без вывода один из вариантов соответствующих расчетных формул:

k1=hf (x, y),.

k2=hf (x+h/2, y+k½),.

k3=hf (x+h/2, y+k2/2), (5).

k4=hf (x+h, y+k3),.

y=z (h)-y (x)=(k1+2k2+2k3+k4).

Отметим, что в этом случае погрешность на шаге пропорциональна пятой степени шага (h5). Отсюда, в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения y'=f (x, y), полученное методом Рунге-Кутта по формулам (5), будет близким к точному.

Эффективная оценка погрешности метода Рунге-Кутта затруднительна. Поэтому для определения правильности выбора шага h на практике обычно на каждом этапе из двух шагов применяют двойной пересчет. А именно, исходя из текущего верного значения y (xi), вычисляют величину y (xi+2h) двумя способами: один раз с шагом h, а другой раз с двойным шагом H=2h. Если расхождение полученных значений не превышает допустимой погрешности, то шаг h для данного этапа выбран правильно и полученное с его помощью значение можно принять за y (xi+2h). В противном случае шаг уменьшают в два раза.

Такого рода вычислительную схему легко запрограммировать для работы на ЭВМ.

Геометрический смысл использования метода Рунге-Кутта с расчетными формулами (5) состоит в следующем. Из точки (xi, yi) сдвигаются в направлении, определяемом углом 1, для которого tg1=f (xi, yi). На этом направлении выбирается точка с координатами (xi+, yi+). Затем из точки (xi, yi) сдвигаются в направлении, определяемом углом 2, для которого.

tg2=f (xi+, yi+),.

и на этом направлении выбирается точка с координатами (xi+, yi+). Наконец, из точки (xi, yi) сдвигаются в направлении, определяемом углом 3, для которого.

tg3=f (xi+, yi+).

и на этом направлении выбирается точка с координатами (xi+h, yi+k3). Этим задается еще одно направление, определяемое углом 4, для которого tg4=f (xi+h, yi+k3). Четыре полученные направления усредняются в соответствии с последней из формул (5). На этом окончательном направлении и выбирается очередная точка (xi+1, yi+1)= (xi+h, yi+y).

Для вычисления по формулам (5) удобно пользоваться схемой, приведенной в таблице 1.

Таблица 1.

i.	x.	y.	k=hf (x, y).	y.
	x0. x0+h/2. x0+h/2. x0+h.	y0. y0+k½. y0+k2/2. y0+k3.	k1. k2. k3. k4.	k1. 2k2 2k3 k4.
;	;	;	;
	x1.	y1.	…	…

Метод Рунге-Кутта обладает значительной точностью и, несмотря на свою трудоемкость, широко используется при численном решении дифференциальных уравнений с помощью ЭВМ. Кроме того, важным преимуществом этого метода является возможность применения «переменного шага» .

Пример: Методом Рунге-Кутта вычислить на отрезке [0; 0,5] интеграл дифференциального уравнения y'=x+y, y (0)=1, приняв шаг h=0,1.

Покажем начало процесса. Вычисление у1. Последовательно имеем:

k1=(0+1)0,1=0,1;

k2=0,05+(1+0,05)0,1=0,11;

k3=0,05+(1+0,055)0,1=0,1105;

k4=0,1+(1+0,1105)0,1=0,12 105.

Отсюда у0=(0,1+20,11+20,1105+0,12 105)=0,1103 и, следовательно,.

дифференциальный уравнение пикар эйлер у1=у0+у0=1+0,1103=1,1103.

Аналогично вычисляются дальнейшие приближения. Результаты вычислений приведены в таблице 2.

Таким образом, у (0,5)=1,7974.

Для сравнения приводим точное решение:

у=2ех-х-1,.

откуда у (0,5)=2е½−1,5=1,79 744…

Таблица 2.