Основные свойства циклоиды

Для начала необходимо выяснить, какая же кривая называется циклоидой.

Рассмотрим круг радиуса a с центром в точке А. Пусть рассматриваемый круг катится без скольжения вдоль оси ОХ. Кривая, описываемая при этом любой точкой окружности, называется циклоидой.

Это определение циклоиды никогда не удовлетворяло ученых: ведь оно опирается на механические понятия — скорости, сложения движений и т. д. Поэтому геометры всегда стремились дать циклоиде «чисто геометрическое определение» Но для того, чтобы дать такое определение, нужно прежде всего изучить основные свойства циклоиды, пользуясь ее механическим определением. Выбрав наиболее простое и характерное из этих свойств, можно положить его в основу геометрического определения.

Начнем с изучения касательной и нормали к циклоиде. Что такое касательная к кривой линии, каждый представляет себе достаточно ясно; поэтому его приводить здесь не будем. Нормалью называется перпендикуляр к касательной, восставленный в точке касания. На рис. 1.1 изображена касательная и нормаль к кривой АВ в ее точке М.

Рис. 1.1.

Рассмотрим циклоиду (рис. 1.2). Круг катится по прямой АВ. Допустим, что вертикальный радиус круга, проходивший в начальный момент через нижнюю точку циклоиды, успел повернуться на угол ц и занял положение ОМ. Иными словами, мы считаем, что отрезок М_оТ составляет такую долю отрезка М_оМ₁, какую угол ц составляет от полного оборота. При этом точка М₀ пришла в точку М.

Рис. 1.2.

Точка М и есть интересующая нас точка циклоиды.

Стрелочка OH изображает скорость движения центра катящегося круга. Такой же горизонтальной скоростью обладают все точки круга, в том числе и точка М. Но, кроме того, точка М принимает участие во вращении круга. Скорость МС, которую точка М на окружности получает при этом вращении, направлена по касательной МС₁ к окружности, т. е. перпендикулярно к радиусу ОМ. А т.к. в этом случае скорость МС по величине равна скорости MP (т. е. скорости ОН). Поэтому параллелограмм скоростей в случае нашего движения будет ромбом (ромб МСКР на рис. 1.2). Диагональ МК этого ромба как раз и даст нам касательную к циклоиде.

Все сказанное дает возможность решить следующую задачу на построение: дана направляющая прямая АВ циклоиды, радиус r производящего круга и точка М, принадлежащая циклоиде (рис. 1.2). Требуется построить касательную МК к циклоиде.

Имея точку М, мы без труда строим производящий круг, в том его положении, когда точка на окружности попадает в М. Для этого предварительно найдем центр О при помощи радиуса МО=r (точка О должка лежать на прямой, параллельной АВ, на расстоянии r от нее). Затем строим отрезок MP произвольной длины, параллельный направляющей прямой. Далее строим прямую МС₁, перпендикулярную к ОМ. На этой прямой откладываем от точки М отрезок МС, равный MP. На МС и MP, как на сторонах, строим ромб. Диагональ этого ромба и будет касательной к циклоиде в точке М.

Это построение — чисто геометрическое, хотя получили мы его, используя понятия механики. Теперь мы можем проститься с механикой и дальнейшие следствия получать без ее помощи. Начнем с простой теоремы.

Теорема 1.Угол между касательной к циклоиде (в произвольной точке) и направляющей прямой равен дополнению до 90° половины угла поворота радиуса производящего круга.

Иными словами, на рис. 1.2.

? KLT равен или.

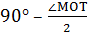
? КМР = .

Это равенство мы теперь докажем. Для сокращения речи условимся угол ц поворота радиуса производящего круга называть «основным углом». Значит, угол МОТ на рис. 1.2 — основной угол. Будем считать основной угол острым. Для случая, когда катящийся круг сделает больше четверти полного оборота, доказательство будет аналогично.

Рассмотрим угол СМР. Сторона СМ перпендикулярна ОМ (касательная к окружности перпендикулярна радиусу). Сторона MP (горизонталь) перпендикулярна к ОТ (к вертикали). Но угол МОP, по условию, острый, а угол СМР — тупой. Значит, углы МОТ и СМР составляют в сумме 180° (углы со взаимно перпендикулярными сторонами, из которых один острый, а другой — тупой).

Итак, угол CMP равен 180° -ц. Но, как известно, диагональ ромба делит угол при вершине пополам. Следовательно, уго.

КМР = 90° -,.

что и требовалось доказать.

Обратим теперь внимание на нормаль к циклоиде. Изобразим левую часть рис. 1.2 крупнее, причем проведем нормаль ME (ME? МК; рис. 1.3).

Из рис. 1.3 следует, что угол ЕМР равен разности углов КМЕ и КМР, т. е. равен 90° - ? KMP.

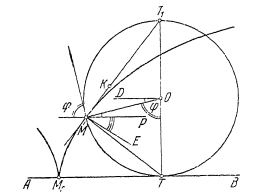
Рис. 1.3.

Но мы только что доказали, что сам угол КМР равен 90° ;

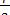
Таким образом, получаем:

? РМЕ = 90° -? КМР = 90° - (90° -) =.

Мы доказали простую, но полезную теорему. Дадим ее формулировку:

Теорема 2. Угол между нормалью к циклоиде (в любой ее точке) и направляющей прямой равен половине «основного угла».

Соединим" точкой (Т) производящего круга теперь точку М («текущую» точку циклоиды) с «нижней (с точкой касания производящего круга и направляющей прямой — рис. 1.3). Треугольник МОТ, очевидно, равнобедренный (ОМ и ОТ — радиусы производящего круга). Сумма углов при основании этого треугольника равна 180° - ц, а каждый из углов при основании — половике этой суммы. Итак, ? OMT = 90° - .

Обратим внимание на угол РМТ. Он равен разности углов ОМТ и ОМР. Мы видели сейчас, что ? OMT равен 90° -; что касается угла ОМР, то нетрудно выяснить, чему он равен. Ведь угол ОМР равен углу DOM (внутренние накрестлежащие углы при параллельных).

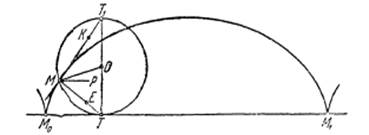
Рис. 1.4.

Непосредственно очевидно, что ? DOM равен 90°- ц. Значит,? OMP= = 90° - ц. Таким образом, получаем:

? РМТ = ? ОМТ — ? ОМР = 90° - - (90° - ц) = .

Получается замечательный результат: угол РМТ оказывается равным углу РМЕ (по теореме 2). Следовательно, прямые ME и МТ сольются! Наш рис. 1.3 сделан не совсем правильно! Правильное расположение линий дано на рис. 1.4.

Сформулируем полученный результат в виде теоремы 3.

Теорема 3 (первое основное свойство циклоиды). Нормаль к циклоиде проходит через «нижнюю» точку производящего круга.

Из этой теоремы получается простое следствие. Угол между касательной и нормалью, по определению, — прямой. Это угол, вписанный в окружность производящего круга. Поэтому он должен опираться на диаметр круга. Итак, ТТ₁— диаметр, и T₁ — «верхняя» точка производящего круга. Сформулируем полученный результат.

Следствие (второе основное свойство циклоиды). Касательная к циклоиде проходит через «верхнюю» точку производящего круга.

Чтобы объяснить это свойство нам необходимо построить циклоиду.

Рис. 1.5.

Построение циклоиды производится в следующей последовательности:

• 1. На направляющей горизонтальной прямой откладывают отрезок АА₁₂, равный длине производящей окружности радиуса r, (2рr);
• 2. Строят производящую окружность радиуса r, так чтобы направляющая прямая была касательной к неё в точке А;
• 3. Окружность и отрезок АА₁₂ делят на несколько равных частей, например на 12;
• 4. Из точек делений 1¹, 2¹, …12¹ восстанавливают перпендикуляры до пересечения с продолжением горизонтальной оси окружности в точках 0₁, 0₂, …0₁₂;
• 5. Из точек деления окружности 1, 2, …12 проводят горизонтальные прямые, на которых делают засечки дугами окружности радиуса r;
• 6. Полученные точки А₁, А₂, …А₁₂ принадлежат циклоиде.

На рис. 1.6 основание циклоиды разделено на 6 равных частей;

Рис. 1.6.

Чем число делений будет больше, тем, чертеж получится точнее. В каждой точке циклоиды, построенной нами, проведем касательную, соединяя точку кривой с «верхней» точкой производящего круга. На нашем чертеже получилось семь касательных (из них две — вертикальные). Проводя теперь циклоиду от руки, будем заботиться, чтобы она действительно касалась каждой из этих касательных: это значительно увеличит точность чертежа. При этом сама циклоида будет огибать все эти касательные).

Проведем на том же рис. 1.6 нормали во всех найденных точках циклоиды. Всего будет, не считая направляющей, пять нормалей. Можно построить от руки огибающую этих нормалей. Если бы мы вместо шести взяли 12 или 16 точек деления, то нормалей на чертеже было бы больше, и огибающая наметилась бы ясней. Такая огибающая всех нормалей играет важную роль при изучении свойств любой кривой линии. В случае циклоиды обнаруживается любопытный факт: огибающей нормалей циклоиды служит точно такая же циклоида, только сдвинутая на 2a вниз и на ра вправо. Этот факт характерен именно для циклоиды.