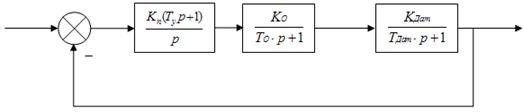
Построить математическую модель АД для статического режима работы

Перед тем, как определить оптимальные параметры настройки П, ПИ, ПИД регуляторов необходимо определить частоту среза объекта, которая находится из выражения для амплитудно-фазовой характеристики объекта управления. АФХ объекта получается после замены оператора р на jщ в заданной передаточной функции объекта.

Уравнения равновесия напряжений с потокосцеплениями в качестве переменных состояния:

Выражение электромагнитного момента через потокосцепления:

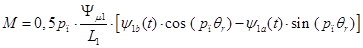
Где:

— электромагнитный момент.

— число пар полюсов.

— потокосцепления соответствующих обмоток.

— потокосцепление магнитов ротора с обмоткой статора.

— величины питающего напряжения соответствующих обмоток.

— активное сопротивление обмоток.

— собственная индуктивность обмоток.

— угол поворота ротор Вычисление угловой скорости вращения ротора:

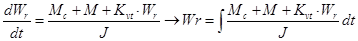
Вычисление угла поворота ротора:

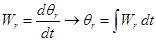
Напряжения питания в вентильном режиме:

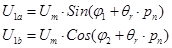
— амплитуда питающего напряжения.

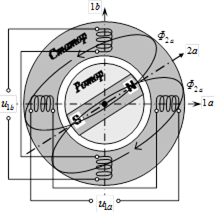
Конструкция двухфазной синхронной машины с постоянными магнитами на роторе.

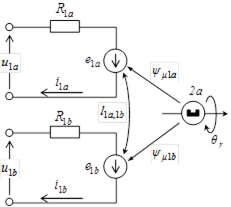
Электрическая схема замещения двухфазной синхронной машины с постоянными магнитами на роторе.

Представленные ниже экспериментальные переходные характеристики объекта h (t) табл.1 с достаточной точностью могут быть аппроксимированы экспоненциальной зависимостью:

где K0 — коэффициент передачи, Т0 — постоянная времени объекта на рис. 4.

Такая временная характеристика соответствует линейной математической модели в виде передаточной функции типового апериодического (инерционного) звена:

W0(p)=.

с достаточно большой инерционностью Т0 = 1000 — 5000 с, которую можно оценить моментом времени с координатой h (T0) = 0.63 hуст, где hуст — установившееся значение h (t) при t> ?.

Коэффициент передачи объекта определяется согласно выражению.

КО=?t°/?U,.

где ?U — приращение входного воздействия, ?t°- соответствующее приращение выходного сигнала. По экспериментальным данным определено К0=11К/В. Постоянная времени Т0=4200 с.

Статическая ошибка при пропорционально-интегральном законе регулирования равна 0.

Пусть коэффициент передачи системы равен, тогда .

Тогда.

.

Составим характеристический многочлен, который является суммой числителя и знаменателя передаточной функции разомкнутой системы, приравняем его к нулю:

Для систем 3-го порядка необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения и то, что произведение средних двух коэффициентов многочлена больше произведения крайних. Таким образом, данная замкнутая система устойчива.

Построим асимптотические ЛЧХ (рис. 7).

Оценим критический коэффициент. Фазовая характеристика пересекает ось на частоте, поэтому .

Запас устойчивости по фазе порядка 60°. Запас устойчивости по амплитуде стремится к +?. Это хорошие показатели, поэтому оставим Кс=0.5. Частота среза, поэтому ожидаемое время регулирования.

.

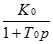
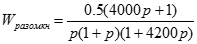
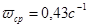
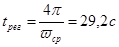
Однако, время регулирования может быть на самом деле в разы меньше, мы лишь оцениваем его порядок. Общепринятые уравнения исполнительного двигателя имеют вид.

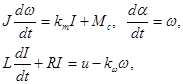
(6).

где — ток, — индуктивность якорной цепи.

Процессы в электрических цепях двигателя протекают существенно быстрее, чем в механических. Поэтому обычно пренебрегают влиянием цепи с передаточной функцией и рассматривают следующие уравнения динамики:

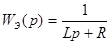
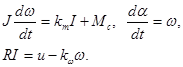
Потери в двигателе в номинальном режиме:

P1н = Р1н — P2н=81 522 — 75 000=6 522, Вт.

Потери на трение:

Pтр = k (п0/1000)2 (D1н/1000)3=3,44 (6Ґ103/103)2 (450/103)3=113, Вт, где:

k = 3+0,5· (D1н -100)/400=3,4375.

Добавочные потери в двигателе:

Pдоб = 0,005P1н=0,005 81 522=408, Вт.

Активное сопротивление обмотки статора при 75С:

R1 = kт R10=1,240,108=0,134, Ом.

где: kт = 1,24 — коэффициент, учитывающий изменение активного сопротивления обмотки статора при нагревании от 15С до 75С.

Потери в обмотках статора:

Pэ1н = 3· I21фн R1=320 020,134=3 855, Вт.

Полная механическая мощность:

Рмех = P2н + Pтр + Pдоб=75 000+133+407,61=75 520, Вт.

Потери в обмотках ротора:

Pэ2н = sн /(1- sн) Рмех=0,017/(1−0,017) 75 520=1 280, Вт.

Потери в стали магнитопровода АД:

Pст = P1нPэ1н — Pэ2н — Pтр — Pдоб=3822 -3855- 1280 -113 — 408 =866, Вт.

Фазный ток статора:

I1ф0 = I1фн · (I10/ I1н)= I1фн kio =200 0,53=52, А.

Линейный ток статора:

I10 = I1ф0 ()1-В=30, А.

Потери в обмотках статора:

Pэ10 = 3· I21ф0 R10=35 220,108=873, Вт.

Мощность, потребляемая двигателем из сети:

P10 = Pэ10 +Pтр +Pдоб +Pст=873+113+408+866 = 2 260, Вт.

Коэффициент мощности:

cos10 = P10 / (U1нI10)=2260/(38 030)=0,115.

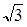
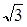
Механическая характеристика при разных значениях амплитуды питающего напряжения В контуре управления анализируемые системы содержат микропроцессорные устройства, работающие с дискретными сигналами, т. е. такие системы являются не непрерывными, а дискретно — непрерывными. Микропроцессорные устройства квантуют непрерывный сигнал и по уровню и по времени. Квантование по уровню происходит потому, что амплитуда дискретного сигнала ограничена некоторой совокупностью значений, определяемой разрядностью микропроцессора. Но квантование по уровню по сравнению с квантованием по времени создает на выходе эффект второго порядка малости, поэтому обычно при рассмотрении динамики системы в первом приближении квантованием по уровню пренебрегают Анализируя влияние квантования сигнала по времени и сравнивая период дискретизации сигнала и величину постоянных времени объекта управления, можно определенно сказать, что исследуемую систему следует рассматривать как непрерывную, так как >.

Структурная математическая модель непрерывной системы управления термическим оборудованием с пропорциональным законом регулирования показана на рисунке ниже.

Рассчитаем переходную характеристику замкнутой САУ с помощью ПП «МОДОС». Для этого построим в программе модель системы, состоящую из источника сигнала, сумматора, интегратора, упругого и апериодического звеньев с коэффициентами многочленов: для источника —, для сумматора —, ,, для интегратора —, ,, для упругого звена —, , для апериодического звена —, .