Яркость и освещённость осевой точки изображения

Равнояркий источник излучения с яркостью L, квадратная площадка площадью S = у² с центром на оси и перпендикулярная оси, стигматически отображается в площадку S' = у' (рис. 6.5). Площадка S настолько мала, что полный телесный угол О пучка во входной зрачок оптической системы D из любой точки предмета можно считать постоянным, как и телесный угол Q' из выходного зрачка /У в любую точку изображения S'.

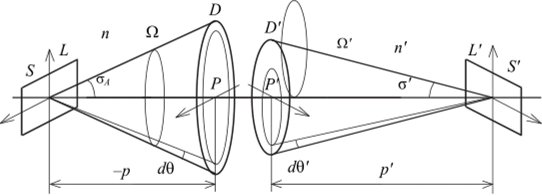
Рис. 6.5.

В отсутствие потерь поток излучения от предмета через оптическую систему равен потоку на площадку изображения.

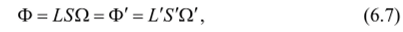
где L' — яркость изображения. Это равенство справедливо как для полного потока энергии, так и для светового, поэтому индексы Е или V не поставлены.

В (6.7) учтено, что в параксиальной области косинусы углов.

наклона лучей к оси «1. В этом же приближении по (6.2) Q * па_А ;

Q' = лст',|'. Выражая в (6.7) площади через стороны квадратов, получаем.

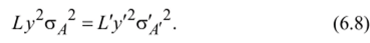
Учитывая, что по теореме Лагранжа-Гельмгольца (см. разд. 2.5) в параксиальной области п уа_А * n’y’o’j, окончательно получаем связь яркости предмета и изображения:

Если оптическая система находится в однородной среде, то яркости предмета и изображения одинаковы.

Лучи из осевой точки предмета, лежащие в конусе, ограниченном углами 0 и 0 + </0, сопряжены с лучами, лежащими в конусе.

0', 0' + <70'. Поток энергии из выбранного конуса пространства предметов перейдёт в конус сопряжённых лучей в пространстве изображений. Можно поэтому доказать, что в общем случае неравнояркого источника сохраняется пропорциональность или равенство угловых зависимостей яркости в сопряжённых направлениях:

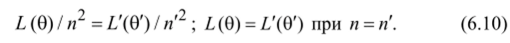
Из (6.7) найдём освещённость осевой точки изображения равнояркого источника:

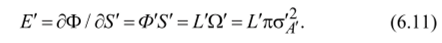
Чем больше апертурный угол с'_А< в пространстве изображений, тем больше освещённость. В фотоаппарате при настройке на бесконечность р а /₀'_б, поэтому освещённость в центре кадрового окна при п = п' и D = D' равна.

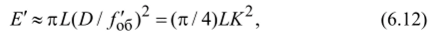
где К = /₀'_б ID- диафрагменное число — величина, обратная относительному отверстию. В ряду диафрагменных чисел 16; 11; 8 и так далее, наносимых на оправах фотообъективов, отношение двух любых соседних чисел равно 1.4. Следовательно, при переходе на соседнее меньшее число освещённость возрастает в 1,4−2 раза.

При о'_А' ~ 1 в (6.11) а_А' следует заменить на sin а'_А'. С увеличением о'_А' > 1 рост sino'^' замедляется. Увеличение диаметров линз объектива, увеличение относительного отверстия в область <�у'_А' > 1, т. е. D / /₀g > 2, нс приведёт к заметному росту освещённости нс только изза геометрического фактора, но и по другим причинам. Во-первых, с увеличением D возрастают аберрации пропорционально D⁵. Увеличение радиуса кружка рассеяния препятствует росту освещённости. Вовторых, для взаимокомпенсации аберраций необходимо усложнять оптическую систему, что ведёт к росту световых потерь. Поэтому следует считать значение D / /_об «2 или 1: 0,5 пределом относительного отверстия фотообъективов. Этот предел практически достигнут.

Сжигание на расстоянии

Оценим возможность создания «гиперболоида инженера Гарина». В фантастическом романе А. Н. Толстого «Гиперболоид инженера Гарина» световой поток от сжигаемых в этом «гиперболоиде» угольных «пирамидок» с помощью зеркал фокусировался на удаленных предметах и поджигал их.

У дуговых ртутных ламп сверхвысокого давления типа ДРШ, ДРИШ яркость излучения сравнима с яркостью Солнца L_v = 1 • 10^ч кд-м" ².

Пусть диаметр светящегося тела источника у = 2 мм. Излучение лампы собирается положительной линзой с относительным отверстием D / /д_б =1, /об = ЮО мм. Оценим освещённость, создаваемую этой системой на экране, удалённом от нее на расстояние 1 км.

С плоскостью экрана следует совмещать изображение светящегося тела лампы. В этом случае радиус кружка изображения каждой точки источника на экране минимален. Минимальна и освещённая площадь, а освещённость изображения максимальна. Это общая закономерность в задачах концентрации энергии излучения: освещённость максимальна в плоскости изображения источника.

В сопряжённых плоскостях, согласно (6.10), яркости равны при «= /?'. Для расчёта освещённости определим угол а'_А'. Удаление изображения от задней главной плоскости ОС a' = /' + z'» I км, т. е. /'"z'wl км. По (3.17) линейное увеличение |p| = z'//' = 10⁴ «1. Тогда |z| = /'/ р» /', т. е. источник расположен практически в переднем фокусе ОС. Тогда апертурный угол в пространстве предметов а_А «D/(2/') = 0,5. Из (3.16) (3 = а_А/а'_А', поэтому а'_А' = <�у_А /|(3| =.

= 5−10^-5 «1. Окончательно освещённость в плоскости изображения равна.

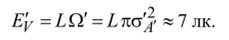
При такой освещённости с трудом можно читать, о воспламенении какого-либо материала не может быть и речи. К тому же, как показано в разд. 2.12, параллельный пучок или почти параллельный с центром в удалённой точке формирует параболическая поверхность, а не гиперболическая.

Причина низкой концентрации — в геометрии формирования пучков: чем дальше плоскость изображения, тем уже конус пучка в точку изображения в соответствии с теоремой Лагранжа-Гельмгольца (см. разд. 2.9). При увеличении размеров светящегося тела пропорционально возрастут размеры изображения, но освещенность при этом нс изменится. Единственный путь повышения освещённости при заданной геометрии — увеличивать яркость источника. Это универсальное решение многих задач энергетики оптического излучения: о передаче максимального потока излучения через малое отверстие [22] или через волоконный световод (см. разд. 6.4.1).