Ход урока. 
Корень n-й степени и его свойства

Приветствие Здравствуйте, ребята. Сегодня на уроке мы познакомимся со следующими понятиями: корень n-ой степени, арифметический корень n-ой степени из числа, с решениями уравнений вида хn=a.

Сейчас ребята, изучившие тему «Квадратные корни», познакомят вас с историей возникновения квадратного корня, термина «радикал», т. е. корень, и напомнят определение квадратного корня.

(Доклад — читает учащийся) Аналогично определим корень n-ой степени. Корнем n-ой степени из числа, а называется такое число, n-ая степень которого равна а.

Примеры:

Корень третьей степени из числа 27 равен 3, т.к. 33=27.

Корень шестой степени из числа 64 равен 2 и (-2), т.к. 26=64 и (-2)6=64.

Согласно данному определению, корень n-ой степени из числа, а — это решение уравнения хn=а. Число корней данного уравнения зависит от n и а.

Рассмотрим функцию f (x)=xn. Эта функция при любом n возрастает на промежутке от нуля до бесконечности и принимает все значения из этого промежутка.

Разминка: Устный счет.

Задаваемые вопросы ученикам:

Вычислить:

• 22
• 23
• 32
• 33
• 42

Актуализация опорных знаний Проблемная ситуация Задача № 1:

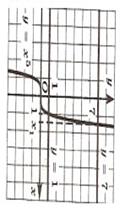
Используя график функции у=х5.

Найти корни уравнения х5=7.

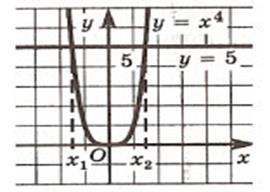
Задача № 2:

Сколько корней имеет уравнение х4=5.

Почему?

Найти эти корни.

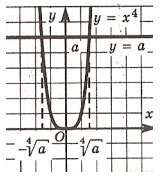
Задача № 3:

Используя график ответить на вопросы:

При каком значении параметра а, уравнение имеет один корень. (Ответ: при а=0).

При каком «а» уравнение имеет два корня? (Овет: при а>0).

При каком «а» уравнение имеет более двух корней. (Ответ: ни при каком значении а) При каком «а» уравнение не имеет корней. (Ответ: при а< 0).

Решение задач обязательного уровня Учащиеся решают задания обязательного уровня по двум вариантам. У доски (оборотная сторона) работу выполняют два учащихся.

Время выполнения работы 10−12 минут, затем происходит проверка результатов вычислений, все учащиеся сравнивают свои ответы, происходит коррекция ЗУН.

В это же время решаются задания среднего уровня, слайд с ходом решения для самопроверки.

Решить уравнение, используя способ замены переменной.

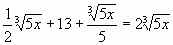Дополнительное задание: Упростите выражение. Ответ: 2,4.

Подведение итогов обобщения материала Ребята, внимание.

• 1. С каким математическим понятием мы работали сегодня — корень n-ой степени
• 2. Что мы применяли для вычислений корня n-ой степени — свойства
• 3. Сколько корней имеет уравнение хn=а, если n — нечетное число — один корень
• 4. Сколько корней имеет уравнение хn=а, если nчетное число — зависит от а:

если, а — отрицательное, то нет корней;

если, а = 0, то один корень;

если, а — положительное, то два корня.

Минута здоровья (гимнастика для глаз) Следующий этап урока контроль знаний учащихся по данной теме, проведение проверочной работы с последующей самопроверкой, слайд Проверочная работа (15−18 минут) Проверочная работа по теме ««Корень n-ой степени и его свойства».

математический арифметический корень радикал.

Вариант I.	Вариант II.
Обязательный уровень (с выбором ответа).	А1. Вычислить: 1) 81; 2) 9; 3) 3;	А1. Вычислить: 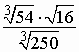1) 1; 2) 2; 3) 20;
А2. Вычислить: -2. 1) -8; 2) 4; 3) -4;	А2. Вычислить. 1) 100; 2) 10; 3) 1;
А3. Вычислить: 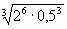1) 50; 2) 25; 3) 5;	А3. Вычислить: -6. 1) — 24; 2) — 12; 3) 12;
А4. Решить уравнение: х6=64. 1) 2; 2) -4; 4 3) -2; 2.	А4. Решить уравнение: х5=32. 1) -2; 2) 2; 3) -2; 2.
Обязательный уровень (указать ответ).	А5. Вычислить: =. Ответ:	А5. Вычислить: Ответ:
А6. Преобразовать выражение: 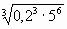=. Ответ:	А6. Преобразовать выражение: 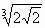Ответ:
Задания с развернутым решением.	В1. Найти значение выражения: 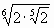Ответ:	В1. Найти значение выражения: 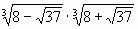=. Ответ:

Критерии оценки:

Правильно выполненные 4 задания — «3».

Правильно выполненные 6 заданий — «4».

Правильно выполненные 7 заданий — «5».

Подведение итогов урока, проверка работ учащимися, выставление оценок.

Ученики обмениваются работами и проверяют по слайду с ответами, подсчитывают правильное количество баллов, выставляют оценку карандашом и сдают учителю для повторной проверки.

Анализируя результаты проверочной работы, учитель подводит итоги урока, выставляет оценки в журнал, задает домашнее задание.

«5» ;

«4» ;

«3» ;

«2»;

Домашнее задание (в зависимости от результатов выполнения проверочной работы).

Слайд. Преподаватель называет фамилии учащихся, и показывает на слайде инд. д/з.

«5» — успешно справились — изучить пункт 33, разобрать примеры № 1 и № 3 из учебника, выполнить по образцу № 417 (а, б), № 419 (а, б);

«3» — допущены ошибки в обязательной части работы — № 391−393 (а, б);

«4» — допущены ошибки в дополнительной части работы — № 394, 410 (а);

«2» — выполняют второй вариант проверочной работы и приносят его на индивидуальную консультацию.