Задачи нелинейного и динамического программирования

Задача нелинейного программирования (ЗНП) состоит в определении максимального или минимального (экстремального) значения функции F (X) = F (x₁… x_n) при условии, что ее переменные удовлетворяют соотношениям:

gi (xi… Xn) < bi (i = 1… k);

gi (xi… Xn) = bi (i = k+1. m). (6.10).

Здесь F (X) и gi (X) -известные функции n переменных (в общем случае нелинейные), bi — заданные числа.

Соотношения (6.10) задают область допустимых значений ЗНП. В отличие от задачи линейного программирования, эта область не всегда является выпуклой.

Решение ЗНП состоит в определении такой точки.

X* = (x₁… x_n) области допустимых решений, в которой функция F (x) достигает экстремального значения, т. е. F (X*) > F (X) или.

F (X*) < F (X) для любых точек Х = (х1. x_n) из области допустимых решений ЗНП. В общем случае решение задачи сводится к определению такой точки Х* области допустимых решений, через которую проходит гиперповерхность максимального (или минимального) уровня: F (X) = H_max (или H_min). Указанная точка может находиться как на границе области допустимых решений, так и внутри ее.

Для случая двух переменных решение ЗНП можно получить с использованием ее геометрической интерпретации путем реализации следующих этапов:

• 1. Построить область допустимых решений.
• 2. Построить гиперповерхность F (X) = H.
• 3. Определить гиперповерхность максимального (минимального) уровня или установить неразрешимость задачи из-за неограниченности функции F (X) на множестве допустимых решений.
• 4. Найти точку X* области допустимых решений, через которую проходит гиперповерхность экстремального значения и определить значение функции F (X) в этой точке — F (X*).

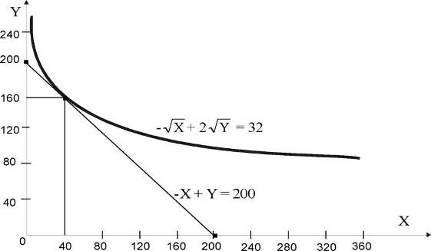
ПРИМЕР Фирма готова инвестировать не более 200 млн руб. в два проекта, А и В. Прибыль от вложения Х млн. руб. в проект, А составит VX млн. руб. от его реализации, прибыль от вложения Y млн. руб. в проект В составит 2л/у млн. руб.

Определить оптимальное распределение суммы инвестиций между проектами, А и В, которое обеспечит максимальную прибыль в результате реализации обоих проектов.

Решение.

Требуется найти максимальное значение функции.

F = VX + 2л/у.

Область допустимых решений задачи — треугольник АВС, ограниченный прямой X + Y = 200 и отрезками [0, 200] на оси ОХ и [0, 200] на оси OY.

Полагая значение функции F (X, Y) равным некоторому числу Н, получаем линии уровня, представленные на рисунке 16.5. С увеличением Н значения функции F увеличиваются.

Гиперповерхность максимального значения F (X, Y) = 32 достигает последнего контакта с областью допустимых решений в граничной точке области допустимых решений Х* = 40, Y* = 160.

Ниже приведена геометрическая интерпретация решения задачи.

Для аналитического решения ЗПН можно применить метод множителей Лагранжа.

Задача динамического программирования (ЗДН) является многоэтапной, на каждом этапе определяется решение некоторой частной задачи.

Предположим, что некоторая организационноэкономическая система ОЭС в начальный момент времени t₀ находится в определенном состоянии S₀. В результате управления U система переходит из своего начального состояния S₀ в конечное состояние S^. Для оценки качества управления системой выбирается функция W = W (U).

Задача состоит в том, чтобы из множества возможных управлений (U) найти такое U*, при котором функция W (U) принимает экстремальное значение W (U*).

Дадим геометрическую интерпретацию ЗДН (рис. 6.4).

Предположим, что состояние ОЭС характеризуется некоторой точкой S на множестве X₁OX₂ параметров этой точки. Под действием управления U эта точка переходит из одного состояния в другое, перемещаясь вдоль линии, определяемой значениями параметров системы S = S (X_b X₂). Каждому управлению U движением точки, т. е. каждой траектории движения точки, поставим в соответствие значение некоторой функции W (U) (например, прибыль предприятия, полученная за планируемое количество лет его работы). Тогда задача состоит в том, чтобы из всех допустимых траекторий развития ОЭС найти такую, которая в результате реализации управления U* обеспечит экстремальное значение функции W (U).

ПРИМЕР Фирме принадлежит n рентабельных предприятий. В начале каждого года она перераспределяет прибыль, полученную от этих предприятий, на финансирование их хозяйственной деятельности в размере (x₁… x_n). Планируется деятельность фирмы на ближайшие m лет.

Задача состоит в определении таких значений (x₁₁… x_ni), (i = 1, 2… m), т. е. в нахождении таких распределений финансовых средств между предприятиями на каждый i-й год (i = 1, 2… m), при которых за m лет обеспечивается получение максимальной прибыли всем предприятиям фирмы.

Постановка задачи Распределение средств между n предприятиями на i-й год (x₁i… x_ni) будем рассматривать как реализацию некоторого управления u₁. Тогда совокупность векторов (x₁₁… x_ni), (i = 1, 2… m) определяет всю совокупность управлений u1, u2. u_m на m шагах распределения средств.

В качестве критерия оценки качества управления взята суммарная прибыль за m лет, которая зависит от всей совокупности управлений: W = W (u₁… u_m).

Следовательно, задача состоит в выборе таких управлений u*, т. е. в таком распределении средств, при котором функция W принимает максимальное значение.

Рассмотрим в общем виде решение ЗДП. Будем считать, что состояние рассматриваемой ОЭС на каждом шаге определяется совокупностью ее параметров Xk = (x₁k, x₂k… x^). Эти параметры были получены в результате реализации управления u_k, обеспечивающего переход системы из (k-1)-ro состояния в k-е состояние. При этом будем полагать, что k-е состояние зависит от предыдущего (k-1)-ro состояния и выбранного управления uk и не зависит от того, каким образом система перешла в это (k-^-е состояние. Напомним, что каждое состояние системы характеризуется набором своих параметров.

Далее будем считать, что если в результате реализации k-го шага получен определенный доход, также зависящий от предыдущего (к-1)-го состояния системы и выбранного управления и равный W (Xk_-1, uk), то общий доход за n шагов составляет.

F =Z W (Xk-_buk). (6.11).

Эти два условия позволяют сформулировать для ЗДП принцип оптимальности, позволяющий устанавливать правило построения для этой задачи оптимальной стратегии управления, т. е. такой совокупности управлений (u₁, u₂… u_n), в результате реализации которой система за n шагов переходит из начального положения в конечное, и при этом функция W принимает максимальное значение.

ПРИНЦИП ОПТИМАЛЬНОСТИ БЕЛЛМАНА Каково бы ни было состояние системы перед очередным шагом, надо выбрать управление на этом шаге таким, чтобы выигрыш на данном шаге и оптимальный выигрыш на всех последующих шагах были максимальными.

Отсюда следует, что оптимальную стратегию управления можно получить, если сначала найти оптимальную стратегию управления на последнем k-м шаге, затем на двух последних шагах и т. д. вплоть до первого шага.

Дадим математическую формулировку принципа оптимальности. Для этого обозначим через F_n(X₀) максимальный доход, полученный за n шагов при переходе системы из начального состояния X0 в конечное состояние X_n при реализации оптимальной стратегии управления U = (u₁… u_n), а через F_n-k (Xk) — максимальный доход, полученный при переходе из любого состояния.

Xk в конечное состояние X_n при оптимальной стратегии управления на оставшихся (n-k) шагах. Тогда можно получить основное функциональное уравнение Беллмана:

Fn-k (Xk) = max [Wk+1(Xk, uk+1) + Fn-k-1(Xk+ 1)] (6.12).

В результате решения этого уравнения путем определенной итерационной процедуры и получаем решение ЗДП.