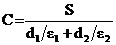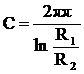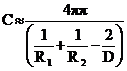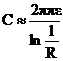Электрическая емкость. 
Теория систем автоматического управления

Электрическая емкость характеризует способность тела или системы тел накапливать электрические заряды, запасая таким образом энергию электрического поля.

Емкость определяют как отношение заряда уединенного проводящего тела к его потенциалу (при условии, что точка, в которой потенциал принимается равным нулю, лежит в бесконечности):

С = q/U,.

а емкость двух проводящих тел, разделенных диэлектриком и заряженных равными по значению и противоположными по знаку зарядами — как отношение абсолютного значения заряда к разности потенциалов этих тел:

С=q/(U₁ — U₂). (1.15).

Емкость зависит от геометрических размеров, конфигурации, диэлектрической проницаемости диэлектрика и взаимного расположения тел.

Емкость измеряется в Фарадах (Ф).

Ниже приведены выражения для емкостей простейших систем.

Емкость плоского конденсатора с однослойным диэлектриком равна:

С = (eS)/d,.

где S — площадь каждой пластины; d — расстояние между пластинами.

Емкость плоского конденсатора с двухслойным диэлектриком с диэлектрической проницаемостью e₁ и e₂ каждого слоя и их толщиной, равной d₁ и d₂ определяется выражением.

.(1.16).

Емкость на единицу длины цилиндрического конденсатора (коаксиального кабеля) с однослойным диэлектриком и радиусами обкладок R₁ и R₂ (R₁2):

.(1.17).

Емкость сферического конденсатора с наружным радиусом внутренней сферической обкладки R₁ и внутренним радиусом внешней сферической обкладки R₂ определяется выражением.

.(1.18).

Емкость уединенного шара радиусом R равна:

С = 4peR. (1.19).

Емкость двух шаров радиусами R₁ и R₂, расположенных на расстоянии D (геометрические и электрические оси совпадают).

.(1.20).

Емкость уединенного цилиндра радиусом R и длиной l:

.

Если длина цилиндра много больше его радиуса (l>>R), то емкость можно определять по приближенной формуле.

. (1.21).

При наличии нескольких заряженных проводников вводят понятие частичных емкостей и эквивалентной емкости системы.

Частичной емкостью называется емкость между двумя проводниками, входящими в систему проводников. Частичную емкость между двумя проводниками определяют как абсолютное отношение заряда одного проводника к разности потенциалов между этими проводниками, когда остальные проводники системы имеют один и тот же потенциал.

Эквивалентная емкость (рабочая) — емкость между двумя проводниками, входящими в систему проводников, учитывающая частичные емкости между парой проводов системы.