Работа изменения объёма (объёмной деформации). Vp-диаграмма

В термодинамике наибольшее значение имеют работы сил давления — работы, определяемые через давление. Определим работу сил давления, которую совершает газ при перемещении поршня. Перемещение поршня приводит к деформации (смещению слоёв газа относительно друг друга) рабочего тела в цилиндре, что характеризуется изменением объёма. Поэтому такую деформацию (в отличие от других видов деформации, например, кручения, сдвига, изгиба) принято называть объёмной деформацией, а работу — работой объёмной деформации, или работой изменения объёма.

Допустим, что газ начал очень медленно (равновесно) расширяться и переместил поршень на расстояние dx, настолько малое, что давление газа p можно считать в течение процесса расширения неизменным. Газ действует на поршень с силой, обусловленной давлением р и направленной от газа к поршню площадью, А в сторону положительного направления оси x (рис. 2.2).

Под действием этой силы на внутренней границе поршня совершаются внутренняя элементарная работа изменения объёма:

= F ds cos 0 = F dx = p A dx = p dV; (2.16).

где dV = Adx — изменение объёма газа в цилиндре.

Формула (2.16) определяет элементарную работу, совершаемую при бесконечно малом приращении объёма. Работа изменения объёма, совершаемая при конечном изменении объёма РТ от V₁ до V₂, вычисляется путём суммирования элементарных работ, т. е. путём интегрирования:

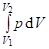
W = W^v =, (2.17).

или для удельной работы изменения объёма.

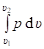
w = w^v =, (2.18).

Равновесный (внутренне равновесный) процесс изменения объёма РТ можно изобразить на Vp-диаграмме в виде кривой 1−2 при движении поршня с трением (необратимый адиабатный процесс) и 1−2s — без трения (обратимый адиабатный процесс) (см. рис. 2.2). Тогда площадь элементарного прямоугольника (выделена мелкой штриховкой) на этой диаграмме, определяемая произведением pdV, будет изображать внутреннюю элементарную работу изменения объёма W, а площадь под кривой процесса 1−2, определяемая как сумма бесконечного числа элементарных прямоугольников, т. е. как интеграл от pdV, будет изображать работу рабочего тела при внутренне равновесном изменении его объёма от V₁ до V₂.

Рисунок 2.2 — К расчёту работы изменения объёма Как видно из рисунка 2.2, внутренняя (индикаторная) работа, совершаемая газом над поршнем в процессе с трением, получается больше (из-за роста давления в результате подвода тепла трения) индикаторной работы, совершаемой газом при его расширении без трения:. Однако в соответствии с (2.8) внешняя (эффективная) работа, отводимая от поршня в окружающую среду в процессе без трения, получается больше эффективной работы с трением:

.

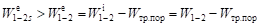
Работа является алгебраической величиной. Знак работы изменения объёма в соответствии с выражениями (2.17) и (2.18) определяется знаками дифференциалов dV и .

При расширении РТ изменение его объёма положительно (dV_рас > 0), а так как давление — существенно положительная величина, то соответственно положительна и работа расширения (W_рас > 0). При сжатии РТ его объём уменьшается (dV_сжат < 0), то в соответствии с (2.17) работа сжатия отрицательна (W_сжат < 0).

Уравнение энергии (ПЗТ) для хаотического движения микрочастиц системы. Если рассматривается только одно хаотическое движение (относительное) микрочастиц системы относительно их центра инерции (точки, относительно которой суммарный импульс всех частиц равен нулю), то балансовые соотношения (2.12) — (2.14) составляются только для изменения внутренней энергии dU системы (подвижной — для выделенного элемента потока или неподвижной — для рабочего тела в цилиндре) и работы изменения объёма (2.16).

Тогда уравнение ПЗТ (2.13) для внутренней (индикаторной) работы запишется в виде.

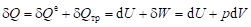
. (2.19).

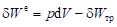
Уравнения ПЗТ (2.12) и (2.14) с учётом выражения (2.8) для эффективной работы запишутся в таком виде:

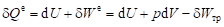
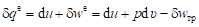
;; (2.20).

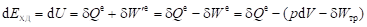
. (2.21).

Из математического (аналитического) выражения (2.20) следует физическое утверждение: внешняя теплота Q^е, подводимая к системе из ОС, идёт на изменение ВЭ dU системы и на совершение системой эффективной (внешней по месту расчёта) работы дW^е над телами ОС. Это утверждение составляет содержание ПЗТ для хаотического (относительного) движения микрочастиц закрытой термодинамической системы (подвижной или неподвижной). Часто считают, что уравнения (4.19) и (4.20) выражают ПЗТ только для неподвижного тела, например, для газа в цилиндре. Однако эти уравнения справедливы и для расчёта изменения ВЭ подвижного элемента среды (подвижной закрытой термодинамической системы), например, элемента потока жидкости, поскольку в этих уравнениях учитывается только относительное движение микрочастиц системы относительно их центра инерции, которое не зависит от того, перемещается ли центр инерции системы или неподвижен.

В случае протекания так называемых обратимых процессов (идеальных, без трения) работа трения и теплота трения равны нулю, внешние теплота и работа равны соответственно внутренним теплоте и работе, а уравнения ПЗТ (2.19) и (2.20) имеют одинаковый вид.

(2.22).

или для удельных величин.

. (2.23).

Однако нужно всегда помнить, что в случае реальных процессов (с трением) в этих уравнениях под теплотой следует понимать полную теплоту, равную сумме внешней теплоты от источников тепла и теплоты трения.

Если к правой части (2.19) прибавить и вычесть d (pV), то получим это же уравнение ПЗТ для хаотического движения в другом виде:

Q = dU + d (pV) + pdV — d (pV) = d (U + pV) — Vdp = dH — Vdp, (2.24).

где Н = U + pV — энтальпия, которая имеет смысл в потоке, в котором величина pV играет роль потенциальной энергии давления, оказываемого соседними слоями подвижной среды на рассматриваемый элемент потока.

Уравнение (2.24) для реальных процессов с трением можно записать через удельные величины.

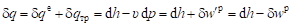
(2.25).

или в интегральном виде.

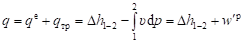
(4.26).

где — удельная энтальпия;

— внутренняя по знаку удельная работа, которую по аналогии с работой изменения объёма можно назвать работой изменения давления;

— внешняя по знаку удельная работа изменения давления В учебниках эту работу называют располагаемой работой и обозначают wo. Критика этого термина дана в [17]. (находится в потоке как работа результирующей сил давления по перемещению элемента среды).

Уравнения (4.24) — (4.26), полученные путём тождественных преобразований уравнения энергии для хаотического движения (4.19), будут так же справедливы как для РТ в цилиндре, так и для подвижного элемента потока.