Оценка функции распределения и построение ее графика

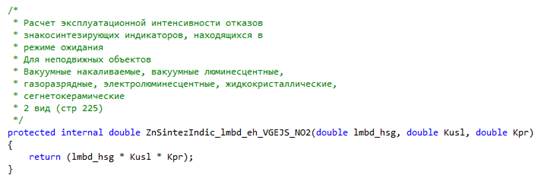
Функцией распределения называется функция.

(Х) = (Х) = (Х <),.

то есть функция распределения равна вероятности того, что случайная величина Х примет значение, меньшее х. Она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения.

Оценкой функции распределения называется функция, задающая для каждого.

Использование данной функции целесообразно при больших значениях n.

Для её нахождения потребуются следующие значения: х, mi — число выборочных значений случайной величины (частота), mx — накопленная частота и щх — накопленная частость.

Накопленная частота — количество вариантов mi, значения которых меньше х.

То есть, сумма текущего и предыдущих значений частоты.

Накопленная частость — отношение накопленной частоты к общему числу наблюдений n.

Так как исследуется непрерывная случайная величина, оценка функции распределения строится по интервальному статистическому ряду. Для этого необходимо найти накопленные частоты и частости. В данном случае значения выборочной функции распределения равны значениям накопленных частостей.

Получаем следующие вычисления (рисунок 11). [см. 1].

Рисунок 11 Нахождение оценки функции распределения Получились следующие значения (рисунок 12).

Рисунок 12 Значения оценки функции распределения Чтобы найти график оценки функции распределения, необходимо построить его по интервалу карманов и интервалу найденных оценок функций распределения (рисунок 13).

Рисунок 13 График оценки функции распределения.

Интерпретация полученных результатов. Предварительный выбор закона распределения доходностей

На данном этапе выполнения курсовой работы, после построения диаграммы и нахождения оценки функции распределения, можно сделать предварительный выбор закона распределения. Вывод о законе распределения можно сделать из вида гистограммы, найденной в части 1.3: она имеет вид графика функции нормально распределённой случайной величины. Далее будет предполагаться, что работа ведётся именно с нормально распределённой случайной величиной.