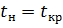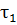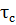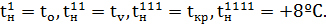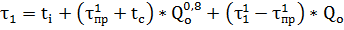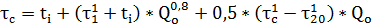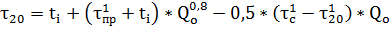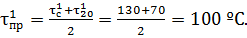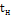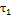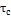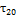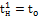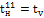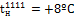Регулирование отпуска тепла

Изменение наружных температур сказывается на потреблении тепла.

Основная цель регулирования — в определении изменения количества тепла абонентом в зависимости от наружной температуры.

Для водяных тепловых сетей, где основной нагрузкой является отопительная нагрузка, принимают центральное качественное регулирование. В зависимости от пункта осуществления различают центральное и местное регулирование.

Центральное регулирование осуществляется на источнике тепла, местное — на абонентских вводах зданий.

Центральное регулирование ведется по одному виду нагрузки, преобладающей в данном районе.

Комбинированный график регулирования сочетает центральное и местное регулирование, качественное и количественное. При центральном качественном регулировании температура воды в подающей магистрали тепловой сети не может снижаться ниже определенного уровня, определяемого условиями работы систем горячего водоснабжения.

При закрытой системе теплоснабжения температура воды в подающей магистрали не может снижаться ниже 70єС, поскольку водопроводная вода должна быть нагрета в системе горячего водоснабжения.

Поэтому температура наружного воздуха, при которой температура сетевой воды в подающей магистрали єС, а регулирование из качественного переходит в количественное, называется точкой излома графика или критической точкой графика ().

При низких температурах наружного воздуха производится центральное качественное регулирование отпуска тепла на отопление.

Для расчета принять следующие обозначения: температура воды в подающей магистрали —; температура воды на входе в систему отопления —; температура обратной воды ;

Расчет графика производится на следующие температурные точки наружного воздуха:

Температура теплоносителя определяется по формуле:

Сетевая вода:

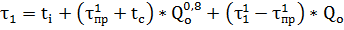
(13).

Теплоноситель на входе в систему отопления:

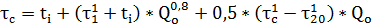
(14).

Теплоноситель на выходе из системы отопления:

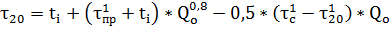
(15).

где: — расчетная внутренняя температура.

— коэффициент понижения температуры теплоносителя.

Расчет графика регулирования отпуска тепла производится по вспомогательным таблицам (6, табл. 4.1; 4.4; 4.6; 4.8.).

Таблица 3 — Регулирование отпуска тепла

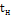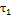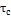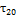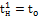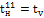-15−13−10 119,6105,9 5 > 14 1 > 2,8 105,9 + 2,8 * 2 = =114,3.	-15 -13−10 79,169,9 5 >10,1 1 > 2,02 69,9 + 2,02 * 2 = = 73,04.	-15−13−15 60,154,3 5 >5,8 1 >1,16 54,3 + 1,16 * 2 = = 97,2.
0,34.	55,25.	59,83.
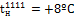+5 +8 +10. 62,348,9 5 >15,5 1 >3,1 62,3 — 3,1 *3 = =53.	+5 +8 +10. 46 36,8 5 >9,2 1 >1,84 46 -1,84 * 3 = = 40,48.	+5 +8 +10. 49,4 39 5 >1,04 1 >2,08 49,4−1,46 * 3 = =34,76.