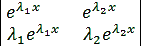Интегрирование однородного линейного уравнения второго порядка с постоянными коэффициентами в случае различных корней характеристического уравнения

Рассмотрим сначала случаи, когда эти корни различные и действительные. Обозначим их через л₁ и л₂. Тогда, подставляя в формулу.

(12.4)y = eлx.

вместо л числа л1 и л2, получим два частных решения уравнения (12.3).

L (y)? y '' + py ' + qy = 0.

y1 =, y1 =. (12.9).

Эти решения, очевидно, линейно независимы, так как их отношение.

=.

не равно тождественно постоянной величине. В линейной независимости решений (12.9).

y1 =, y1 =.

можно убедиться также при помощи определителя Вронского. Имеем.

W (x) = = (л2 — л1)? 0.

Следовательно, частные решения y₁ =, y₁ = образуют фундаментальную систему решений. Тогда общим решением уравнения (12.3).

L (y)? y '' + py ' + qy = 0 будет.

y = C1 + C2 .

Предположим теперь, что корни характеристического уравнения комплексные. Так как коэффициенты этого уравнения действительные, то эти комплексные корни являются сопряженными, так что они имеют вид л1 = a + bi, л2 = a — bi.

Подставляя корень л1 = a + bi в формулу (12.4)y = eлx,.

получим комплексное решение.

y = e (a + bi) x. (12.10).

Но.

e (a + bi) x = eax eibx = eax (cos ax + i sin bx),.

поэтому решение (12.10).

y = e (a + bi) x можно записать так:

y = eaxcos ax + i eaxsin bx. (12.11).

Отделяя в комплексном решении (12.11).

y = eaxcos ax + i eaxsin bx.

действительную и мнимую части, получим два действительных частных решения.

y1 = eaxcos ax, y2 = eaxsin bx. (12.12).

Эти решения, очевидно, независимы, так как.

? const.

Аналогично убеждаемся, что сопряженному корню л2 = a — bi.

соответствуют действительные частные решения.

eaxcos ax, — eaxsin bx. (12.13).

Если корни л1 и л2 чисто мнимые, т. е. л1 = ib? и? л2 = - ib,? то им соответствуют линейно независимые частные решения вида.

y1 = C1 cos ax, ?y2 = C2 sin bx. (12.14).

Эти решения образуют фундаментальную систему решений уравнения (12.3).

L (y)? y '' + py ' + qy = 0, а.

y = C1cos ax + C2sin bx.

есть общее решение этого уравнения.

Случай кратных корней характеристического уравнения Предположим теперь, что характеристическое уравнение (12.8).

л2 + pл + q = 0.

имеет равные корни л1 = л2 = - .

Нам надо найти два линейно независимых частных решения. Одним частным решением, очевидно, будет.

y1 = (12.15).

y1 =. (12.15, а) Убедимся непосредственной подстановкой в уравнение (12.3).

L (y)? y '' + py ' + qy = 0 в том, что.

y2 = x (12.16).

есть второе частное решение уравнения (12.3).

L (y)? y '' + py ' + qy = 0,.

линейно независимое с решением (12.15).

y1 = :

= - x,.

= - p + x. (12.17).

Поэтому.

L (x) = - px + x + px — x + qx = - + q x? 0 (12.18).

— q = 0.

Общим решением уравнения (12.3).

L (y)? y '' + py ' + qy = 0 будет.

y = (C1 + C2x).

Подбор частных решений линейного неоднородного дифференциального уравнения с постоянными коэффициентами и со специальной правой частью.