Линзы Френеля. 
Линзы Френеля, их расчет, моделирование и применение

Линза Френеля — сложная составная линза. Состоит не из цельного шлифованного куска стекла со сферической или иными поверхностями (как обычные линзы), а из отдельных, примыкающих друг к другу концентрических колец небольшой толщины, которые в сечении имеют форму призм специального профиля. Предложена Огюстеном Френелем.

Эта конструкция обеспечивает малую толщину (а следовательно, и вес) линзе Френеля даже при большой угловой апертуре. Сечения колец у линзы строятся таким образом, что сферическая аберрация линзы Френеля невелика, лучи от точечного источника, помещённого в фокусе линзы, после преломления в кольцах выходят практически параллельным пучком (в кольцевых линзах Френеля).

Расчет линз Френеля

Линза Френеля — один из первых приборов, действие которого основано на физическом принципе дифракции света.

Данный прибор, и по сей день не утерял своего практического значения. Общая схема физической модели, на которой основано его действие, представлена на (рис. 1).

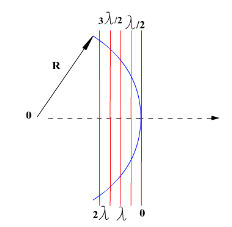
Рис. 1 Схема построения зон Френеля для бесконечно удаленной точки наблюдения (плоская волна).

Примем, что в точке О расположен точечный источник оптического излучения длины волны l. Естественным образом, как всякий точечный источник, он излучает сферическую волну, волновой фронт которой и изображен на рисунке окружностью. Зададимся условием изменить данную волну на плоскую, которая будет распространяться вдоль пунктирной оси. Несколько волновых фронтов этой изменяемой волны, отстающих друг от друга на l/2, изображены на (рис. 1). Для начала отметим, что рассматриваем изменяемую плоскую волну из имеющейся сферической в свободном пространстве. Поэтому, в соответствие с принципом Гюйгенса-Френеля, «источниками» данной изменяемой волны могут служить лишь электромагнитные колебания в имеющейся. И если это не устраивает пространственное распределение фазы этих колебаний, то есть волновой фронт (сферический) исходной волны. Давайте попробуем его подкорректировать. Проведем все по действиям.

Действие первое: заметим, что с точки зрения вторичных волн Гюйгенса — Френеля (которые сферические) пространственное смещение на целую длину волны в любом направлении не меняет фазы вторичных источников. Поэтому мы можем позволить себе например «разорвать» волновой фронт исходной волны как показано на (рис. 2).

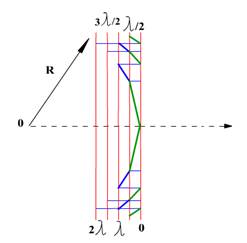
Рис. 2 Эквивалентное распределение фазы вторичных излучателей в пространстве.

Таким образом, мы «разобрали» исходный сферический волновой фронт на «кольцевые запчасти» номер 1, 2… и так далее. Границы этих колец, называемых зонами Френеля, определяются пересечением волнового фронта исходной волны с последовательностью смещенных друг относительно друга на l/2 волновых фронтов «проектируемой волны». Получившаяся картинка уже существенно «попроще», и представляет собой 2 слегка «шероховатых» плоских вторичных излучателя (зеленый и красный на рис. 2), которые однако, гасят друг друга из-за упомянутого полуволнового взаимного смещения.

Итак, мы видим, что зоны Френеля с нечетными номерами не только не способствуют выполнению поставленной задачи, но даже активно вредительствуют. Способов борьбы с этим два.

Первый способ (амплитудная линза Френеля). Можно данные нечетные зоны просто геометрически закрыть непрозрачными кольцами. Так и делается в крупногабаритных фокусирующих системах морских маяков. Конечно, этим можно не добиться идеальной коллимации пучка. Можно увидеть, что оставшаяся, зеленая, часть вторичных излучателей во-первых, не совсем плоская, а во-вторых разрывная (с нулевыми провалами на месте бывших нечетных зон Френеля).

Поэтому строго коллимированная часть излучения (а ее амплитуда — ни что иное как нулевая двумерная Фурье-компонента пространственного распределения фазы зеленых излучателей по плоскому волновому фронту с нулевым смещением, см. (рис. 2) будет сопровождаться широкоугловым шумом (все остальные Фурье-компоненты кроме нулевой). Поэтому линзу Френеля почти нереально использовать для построения изображений — только для коллимации излучения. Однако, тем не менее коллимированная часть пучка будет существенно мощнее, чем в отсутствие линзы Френеля, поскольку мы по крайней мере избавились от отрицательного вклада в нулевую Фурье-компоненту от нечетных зон Френеля.

Второй способ (фазовая линза Френеля). Можно сделать кольца, закрывающие нечетные зоны Френеля, прозрачными, с толщиной, соответствующей дополнительному фазовому набегу l/2. В таком случае волновой фронт «красных» вторичных излучателей сместится и станет «зеленым», см. рис. 3.

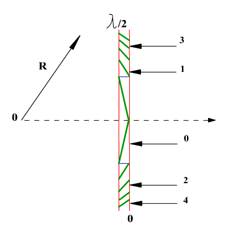
Рис. 3 Волновой фронт вторичных излучателей за фазовой линзой Френеля.

Реально фазовые линзы Френеля имеют два варианта исполнения. Первый представляет собой плоскую подложку с напыленными полуволновыми слоями в областях нечетных зон Френеля (более дорогостоящий вариант). Второй — это объемная токарная деталь (или даже полимерная штамповка по единожды сделанной матрице, вроде грампластинки), исполненная в виде «ступенчатого конического пьедестала» со ступенькой в полдлины волны фазового набега.

Таким образом, Френелевские линзы позволяют справиться с колимацией пучков большой поперечной апертуры, одновременно являясь плоскими деталями небольшого веса и относительно небольшой сложности изготовления. Эквивалентная по эффективности обычная стеклянная линза для маяка весит с полтонны и стоит немногим дешевле, чем линза для астрономического телескопа.

Обратимся теперь к вопросу о том, что произойдет при смещении источника света вдоль оси относительно линзы Френеля, спроектированной исходно для коллимации излучения источника в положении О (рис. 1). Исходное расстояние от источника до линзы (то есть исходную кривизну волнового фронта на линзе) заранее условимся называть фокусным расстоянием F по аналогии с обычной линзой, см. (рис. 4).

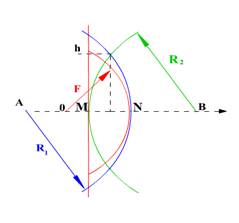
Рис. 4 Построение изображения точечного источника линзой Френеля.

Итак, чтобы при смещении источника из положения О в положение, А линза Френеля продолжала быть линзой Френеля, нужно, чтобы границы зон Френеля на ней остались прежними. А эти границы — это расстояния от оси, на котором пересекаются волновые фронты падающей и «проектируемой» волны. Исходно падающая имела фронт с радиусом кривизны F, а «проектируемая» была плоской (красным цветом на рис. 4). На расстоянии h от оси эти фронты пересекаются, задавая границу какой-то из зон Френеля,.

MN=nl/2,.

где n — номер зоны, начинающейся на этом расстоянии от оси.

При перемещении источника в точку, А радиус падающего волнового фронта увеличился и стал R1 (синий цвет на рисунке). Значит, нам надо придумать новую поверхность волнового фронта, такую, чтобы она пересеклась с синей на том же расстоянии h от оси, дав то же MN на самой оси. Мы подозреваем, что такой поверхностью проектируемого волнового фронта может быть сфера с радиусом R2 (зеленый цвет на рисунке). Докажем это.

Расстояние h легко рассчитывается из «красной» части рисунка:

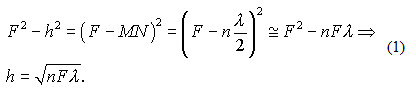
Здесь мы пренебрегаем малым квадратом длины волны по сравнению с квадратом фокуса — приближение, полностью аналогичное параболическому приближению при выводе обычной формулы тонкой линзы. С другой стороны, мы хотим найти новую границу n-й зоны Френеля в результате пересечения синего и зеленого волновых фронтов, назовем ее h1. Исходя из того, что мы требуем прежней длины отрезка MN:

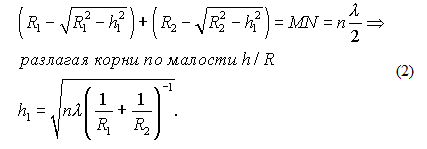
Наконец, требуя h=h1, получаем:

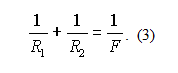
Это уравнение совпадает с обычной формулой тонкой линзы. Более того, оно не содержит номера n рассматриваемой границы зон Френеля, а значит, справедливо для всех зон Френеля.

Таким образом, мы видим, что линза Френеля может не только коллимировать пучки, но и строить изображения. Правда, нужно иметь ввиду, что линза все-таки ступенчатая, а не непрерывная. Поэтому качество изображения будет заметно ухудшено за счет примеси высших Фурье-компонент волнового фронта, обсуждавшихся в начале этого раздела.

То есть линзу Френеля можно использовать для фокусирования излучения в заданную точку, но не для прецизионного построения изображений в микроскопических и телескопических устройствах.

Все вышесказанное относилось к монохроматическому излучению. Однако можно показать, что путем аккуратного выбора диаметров обсуждавшихся колец можно добиться разумного качества фокусировки и для естественного света. 5] [6] [7].