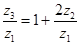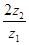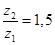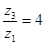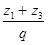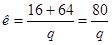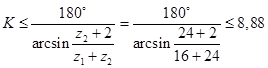Проектирование кинематической схемы планетарного редуктора

Модуль зубчатых колес планетарного механизма m₁ = 3,5 мм;

Число зубьев колес простой передачи.

z_a =12; z_b = 18;

Модуль зубчатых колес z_a и z_b m=8 мм;

Редуктор двухступенчатый.

Передаточное отношение планетарной ступени редуктора равно Подбор чисел зубьев и числа сателлитов однорядного планетарного механизма проводится в следующей последовательности:

а) из условия соосности z₃ = z₁+2z₂ и из формулы передаточного отношения.

выразить отношение и установить, какое из колес, 1 и 2, меньшее.

5= 1+

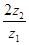
4= 1+.

отсюда z₁ < z₂;

Задавшись числом зубьев меньшего колеса z₁ =16 (т.к. z_min?15) определим число зубьев второго колеса.

z₂ = ;

принимаем z₁ =24.

Учитывая, найдем z₃ = z₁ · 4= 64

Принимаем z₃ = 64.

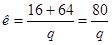
б) из условия сборки к = определяем ряд возможных значений для числа сателлитов к (q — целое число).

При к = 2 q = 40.

к = 4 q = 20.

к = 8 q = 10.

в) по условию соседства.

Предельно допустимое число сателлитов равно 8. Для проектируемого планетарного редуктора можно принять число сателлитов, равное 2, 4 и 8. Примем количество сателлитов равным 4. Окончательное решение по количеству сателлитов принимается из расчета колес на прочность (курс деталей машин).

Размеры колес по делительным окружностям равны.

r₁ = m₁ · z₁ = 3,5 • 16 = 56 мм;

r₂ = m₁ · z₂ = 3,5 • 24 = 84 мм;

r₃ = m₁ · z₃ = 3,5• 48 = 168 мм;

Колеса второй ступени планетарного редуктора имеют эти же размеры. По полученным данным строится кинематическая схема на листе 4.