Кинетическая энергия механической системы и её связь с работой

Рассмотрим простейшую систему, состоящую из одной частицы (материальной точки) массы m, движущейся под действием сил, результирующая которых равна .

Запишем уравнение движения частицы:

.

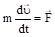
Умножим скалярно обе части этого равенства на элементарное перемещение частицы :

.

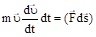
. (3.7).

Скалярное произведение распишем через модули векторов и косинус угла между ними.

.

Поскольку косинус угла между векторами и равен единице, то равенство (3.7) перепишется в виде.

. (3.8).

Произведение md равно производной от величины, т. е.

.

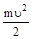
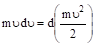
Заменив полученным выражением левую часть формулы (3.8), придем к соотношению.

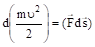
. (3.9).

Если результирующая сил, действующих на частицу, равна нулю,.

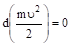
то сама величина.

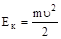
(3.10).

остается постоянной.

Эта величина называется кинетической энергией частицы.

Приняв во внимание, что произведение равно модулю импульса частицы р, выражению (3.10) можно придать вид.

.

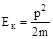
Если сила F, действующая на частицу не равна нулю, кинетическая энергия получит за время dt приращение.

(3.11).

где ds — перемещение частицы за время dt.

Величина называется работой, совершаемой силой на пути (ds — модуль перемещения). Из (3.11) следует, что работа характеризует изменение кинетической энергии, обусловленное действием силы на движущуюся частицу:

.

Проинтегрируем (т.е. просуммируем) обе части равенства (3.9) вдоль траектории движения частицы от точки 1 до точки 2:

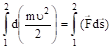
. (3.12).

Левая часть равенства представляет собой приращение кинетической энергии частицы.

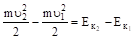
. (3.13).

Правая часть есть работа А₁₂ силы на пути 1−2.

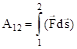
. (3.14).

Подставляя (3.13) и (3.14) в соотношение (3.12), получим.

.

Таким образом, работа результирующей всех сил, действующих на частицу, идет на приращение кинетической энергии частицы. Энергия, так же, как и работа, в системе СИ измеряется в джоулях (Дж):

.

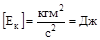
Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку Если частица в каждой точке пространства подвержена воздействию других тел, то говорят, что частица находится в поле сил. Так, например, частица вблизи поверхности Земли находится в поле сил тяжести. В каждой точке пространства на нее действует сила, равная произведению массы на ускорение силы тяжести, т. е. mg.

Пусть заряженная частица находится в электрическом поле точечного заряда q. Это поле характерно тем, что направление силы, действующей на частицу в любой точке пространства, проходит через неподвижный центр (заряд q), а величина силы зависит только от расстояния до этого центра: F=F®. Поле сил, обладающих таким свойством, называется центральным. Поле сил тяжести является частным случаем центрального поля сил (с центром, расположен-ным в бесконечности).

Если в каждой точке поля сила, действующая на частицу, одинакова по величине и направлению (=сonst), поле называется однородным.

Силовое поле можно описать с помощью функции П (x, y, z, t) такой, что компоненты силы в декартовой системе координат равны.

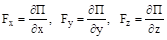
. (3.15).

Такое поле называется потенциальным. Функция П (x, y, z, t) носит название потенциальной функции (или потенциала). Поле, не изменяющееся со временем, называется стационарным. В этом случае П=П (x, y, z). Поле, изменяющееся со временем, называется нестационарным. В этом случае П=П (x, y, z, t). Известно, что если обозначить — скалярную функцию координат x, y, z, то.

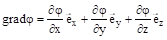
(3.16).

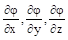
где — орты координат. Вектор с компонентами называется градиентом функции и обозначается символом grad или символический вектор, (набла) — называется оператором Гамильтона. читается «набла фи».

Сравнивая (3.15) и (3.16), можно видеть, что в случае потенциального силового поля.

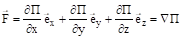
. (3.17).

Подставляя (3.17) в выражение для работы, получим.

.

.

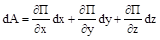
Если поле стационарно, то правая часть этого уравнения представляет собой полный дифференциал функции П (x, y, z,). Следовательно, работа, совершенная над частицей в стационарном силовом поле:

. (3.18).

Проинтегрируем соотношение (3.18) вдоль некоторой траектории от точки 1 до точки 2:

.

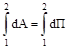
Левая часть этой формулы дает работу А₁₂, совершенную силами поля на пути 1−2. Сумма элементарных приращений dП функции П равна полному приращению этой функции на пути 1−2:

.

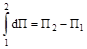
Таким образом, работа на пути 1−2 равна полному приращению функции П на пути 1−2:

А₁₂=П₂-П₁. (3.19).

Форма траектории, по которой осуществлялось интегрирование, была совершенно произвольна. Отсюда заключаем, что работа, совершаемая над частицей силами стационарного потенциального поля, не зависит от пути, по которому движется частица, а определяется только начальным и конечным положением частицы в пространстве.

Силы, работа которых не зависит от пути, по которому частицы переходят из одного положения в другое, называется консервативными. Силы, действующие на частицу в стационарном потенциальном поле, являются консервативными. Работа консервативных сил на замкнутом пути равна нулю.

Консервативными силами являются силы тяготения, силы упругости, силы электростатического происхождения, так как их работа не зависит от формы пути.

В формуле (3.19), определяющей работу, совершенную силами поля на пути (1−2) П₁ и П₂ — значения потенциальной функции П (x, y, z) в начальной и конечной точках. Эта работа идет на приращение кинетической энергии частицы:

. (3.20).

Обозначим — П (x, y, z)=E_п. Соотношение (3.20) примет вид.

;

.

Полученный результат означает, что величина (E_к+E_п) для частицы, находящейся в поле консервативных сил, остается постоянной (является интегралом движения). Слагаемое E_к есть кинетическая энергия частицы. Все величины в (3.19) имеют одинаковую размерность — размерность энергии. Функцию E_п(x, y, z) называют потенциальной энергией частицы во внешнем поле сил. Величину Е, равную сумме кинетической и потенциальной энергии частицы, называют полной механической энергией частицы.

В равенстве (3.19) П (x, y, z) заменим наE_п(x, y, z), получим.

.

Работа, совершаемая над частицей консервативными силами, равна убыли потенциальной энергии частицы. Иначе, работа, совершается за счет запаса потенциальной энергии.

Заменив в соотношении (3.18) функцию П (x, y, z) потенциальной энергией, найдем связь между потенциальной энергией и силой:

.

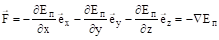
Таким образом, сила, действующая на частицу в стационарном потенциальном силовом поле, равна градиенту потенциальной энергии в данной точке, взятому с обратным знаком. Компоненты силы определяются следующими выражениями:

.

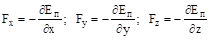
Конкретный вид функции E_п(x, y, z) зависит от характера силового поля. Чтобы найти потенциальную энергию частицы в поле силы тяжести (рис. 3.3), вспомним, что работа, совершаемая над частицей силами этого поля, равна.

;

.

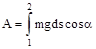
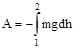
С другой стороны, .

h.