Эквивалентные преобразования пассивных участков электрических цепей

Сопротивления в электрических цепях могут быть соединены последовательно, параллельно, по смешанной схеме и по схемам «звезда», «треугольник».

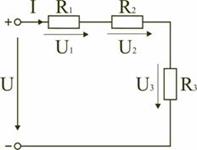
Электрическая цепь с последовательным соединением элементов Рис. 6.

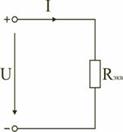
Рис. 7.

Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 6).

На основании второго закона Кирхгофа общее напряжение U всей цепи равно сумме напряжений на отдельных участках:

U = U₁ + U₂ + U₃ или IR_экв = IR₁ + IR₂ + IR₃,.

откуда следует:

R_экв = R₁ + R₂ + R₃.

Цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R_экв (рис. 7). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома.

.

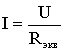
и затем рассчитывают падение напряжений U₁, U₂, U₃ на соответствующих участках электрической цепи (рис. 8). Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.

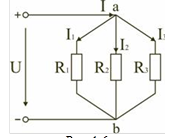
Рис. 8.

Электрическая цепь с параллельным соединением элементов Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 7).

В этом случае они присоединены к двум узлам цепи, а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:

I = I₁ + I₂ + I₃, т. е.

.

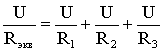
откуда следует, что.

.

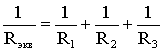
В том случае, когда параллельно включены два сопротивления R₁ и R₂, они заменяются одним эквивалентным сопротивлением.

.

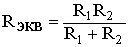
Из соотношения следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

G_экв = G₁ + G₂ + G₃.

По мере роста числа параллельно включенных потребителей проводимость цепи G_экв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 8).

U = IR_экв = I₁R₁ = I₂R₂ = I₃R₃.

Отсюда следует, что.

.

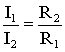
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений. Для цепи, представленной на рис. 9, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми:

R₁=R₂=R₃=R₄=R₅=R.

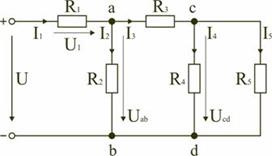
Рис. 9.

Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

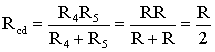
В этом случае исходную схему можно представить в следующем виде:

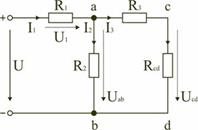
Рис. 10.

На схеме (рис. 10) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

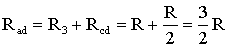
Тогда схему можно представить в сокращенном варианте:

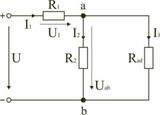
Рис. 11.

На схеме (рис. 11) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно.

.

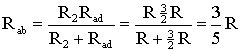
Схему (рис. 12) можно представить в упрощенном варианте (рис. 13), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы будет равно:

.

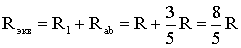
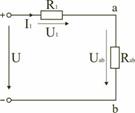
Рис. 12.

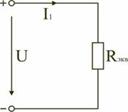
Рис. 13.

В результате преобразований исходная схема представлена в виде схемы (рис. 13) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.