Характеристики рассеяния. 
Элементы статистических исследований

Характеристики положения описывают центр распределения. В то же время значения вариант могут группироваться вокруг него как в широкой, так и в узкой полосе. Поэтому для описания распределения необходимо охарактеризовать диапазон изменения значений признака. Для описания диапазона варьирования признака используются характеристики рассеяния. Наиболее широкое применение нашли размах вариации, дисперсия, стандартное отклонение и коэффициент вариации.

Размах вариации определяется как разность между максимальным и минимальным значением признака в изучаемой совокупности:

R=xmax-xmin.

Очевидным достоинством рассматриваемого показателя является простота расчета. Однако поскольку размах вариации зависит от величин только крайних значений признака, то область его применения ограничена достаточно однородными распределениями. В остальных случаях информативность этого показателя весьма невелика, поскольку существует очень много распределений, сильно отличающихся по форме, но имеющих одинаковый размах. В практических исследованиях размах вариации используется иногда при малых (не более 10) объемах выборки. Так, например, по размаху вариации легко оценить, насколько различаются лучший и худший результаты в группе спортсменов.

В рассматриваемом примере: R=16,36 — 13,04=3,32 (м).

Второй характеристикой рассеяния является дисперсия. Дисперсия представляет собой средний квадрат отклонения значения случайной величины от ее среднего значения. Дисперсия есть характеристика рассеяния, разбросанности значений величины около ее среднего значения. Само слово «дисперсия» означает «рассеяние».

При проведении выборочных исследований необходимо установить оценку для дисперсии. Дисперсия, вычисляемая по выборочным данным, называется выборочной дисперсией и обозначается S2.

На первый взгляд наиболее естественной оценкой для дисперсии является статистическая дисперсия, вычисленная, исходя из определения, по формуле:

.

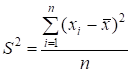
В этой формуле — сумма квадратов отклонений значений признака хi от среднего арифметического. Для получения среднего квадрата отклонений эта сумма поделена на объем выборки п.

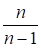
Однако такая оценка не является несмещенной. Можно показать, что сумма квадратов отклонений значений признака для выборочного среднего арифметического меньше, чем сумма квадратов отклонений от любой другой величины, в том числе от истинного среднего (математического ожидания). Поэтому результат, получаемый по приведенной выше формуле, будет содержать систематическую ошибку, и оценочное значение дисперсии окажется заниженным. Для ликвидации смещения достаточно ввести поправочный коэффициент. В результате получается следующее соотношение для оценочной дисперсии:

.

При больших значениях n, естественно, обе оценки — смещенная и несмещенная — будут различаться очень мало и введение поправочного множителя теряет смысл. Как правило, уточнение формулы для оценки дисперсии следует производить при n<30.

В случае сгруппированных данных последнюю формулу для упрощения вычислений можно привести к следующему виду:

.

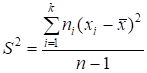
где k — число интервалов группировки;

ni — частота интервала c номером i;

xi — срединное значение интервала c номером i.

В качестве примера проведем вычисление дисперсии для сгруппированных данных разбираемого нами примера (см. табл. 4.):

S2=[4 (13,375−14,5331)2+8 (14,045−14,5331)2+10 (14,715−14,5331)2+.

5 (15,385−14,5331)2+2 (16,055−14,5331)2]/28=0,5473 (м2).

Дисперсия случайной величины имеет размерность квадрата размерности случайной величины, что затрудняет ее интерпретацию и делает не очень наглядной. Для более наглядного описания рассеяния удобнее пользоваться характеристикой, размерность которой совпадает с размерностью исследуемого признака. С этой целью вводится понятие стандартного отклонения (или среднего квадратического отклонения).

Стандартным отклонением называется положительный корень квадратный из дисперсии:

.

В разбираемом нами примере стандартное отклонение равно (м).

Стандартное отклонение имеет те же единицы измерения, что и результаты измерения исследуемого признака и, таким образом, оно характеризует степень отклонения признака от среднего арифметического. Иными словами, оно показывает, как расположена основная часть вариант относительно среднего арифметического.

Стандартное отклонение и дисперсия являются наиболее широко применяемыми показателями вариации. Связано это с тем, что они входят в значительную часть теорем теории вероятностей, служащей фундаментом математической статистики. Помимо этого, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов на вариацию исследуемого признака.

Помимо абсолютных показателей вариации, которыми являются дисперсия и стандартное отклонение, в статистике вводятся относительные. Наиболее часто применяется коэффициент вариации. Коэффициент вариации равен отношению стандартного отклонения к среднему арифметическому, выраженному в процентах:

.

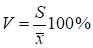
Из определения ясно, что по своему смыслу коэффициент вариации представляет собой относительную меру рассеяния признака.

Для рассматриваемого примера: .

Коэффициент вариации широко используется при проведении статистических исследований. Будучи величиной относительной, он позволяет сравнивать колеблемости как признаков, имеющих различные единицы измерения, так одного и того же признака в нескольких разных совокупностях с различными значениями среднего арифметического.

Коэффициент вариации используется для характеристики однородности полученных экспериментальных данных. В практике физической культуры и спорта разброс результатов измерений в зависимости от значения коэффициента вариации принято считать небольшим (V 20%).

Ограничения на использование коэффициента вариации связаны с его относительным характером — определение содержит нормировку на среднее арифметическое. В связи с этим при малых абсолютных значениях среднего арифметического коэффициент вариации может потерять свою информативность. Чем ближе значение среднего арифметического к нулю, тем менее информативным становится этот показатель. В предельном случае среднее арифметическое обращается в ноль (например, температура) и коэффициент вариации обращается в бесконечность независимо от разброса признака. По аналогии со случаем погрешности можно сформулировать следующее правило. Если значение среднего арифметического в выборке больше единицы, то использование коэффициента вариации правомерно, в противном случае для описания разброса опытных данных следует использовать дисперсию и стандартное отклонение.

В заключение этой части рассмотрим оценку варьирования значений оценочных характеристик. Как уже было отмечено, значения характеристик распределения, рассчитанные по данным эксперимента, не совпадают с их истинными значениями для генеральной совокупности. Точно установить последние не представляется возможным, поскольку, как правило, невозможно обследовать всю генеральную совокупность. Если использовать для оценки параметров распределения результаты разных выборок из одной и той же генеральной совокупности, то окажется, что эти оценки для разных выборок отличаются друг от друга. Оценочные значения флуктуируют около своих истинных значений.

Отклонения оценок генеральных параметров от истинных значений этих параметров называются статистическими ошибками. Причиной их возникновения является ограниченный объем выборки — не все объекты генеральной совокупности входят в нее. Для оценки величины статистических ошибок используется стандартное отклонение выборочных характеристик.

В качестве примера рассмотрим наиболее важную характеристику положения — среднее арифметическое. Можно показать, что стандартное отклонение среднего арифметического определяется соотношением:

.

где у — стандартное отклонение для генеральной совокупности.

Поскольку истинное значение стандартного отклонения не известно, то для оценки стандартного отклонения выборочного среднего используется величина, называемая стандартной ошибкой среднего арифметического и равная:

.

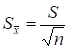
Величина характеризует ошибку, которая в среднем допускается при замене генерального среднего его выборочной оценкой. Согласно формуле, увеличение объема выборки при проведении исследования приводит к уменьшению стандартной ошибки пропорционально корню квадратному из объема выборки.

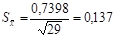
Для рассматриваемого примера значение стандартной ошибки среднего арифметического равно. В нашем случае она оказалась в 5,4 раза меньше значения стандартного отклонения.

Характеристики формы

При проведении статистических исследований встречаются распределения, имеющие самые разнообразные формы. Для характеристики отклонения формы распределения от симметричной используется коэффициент асимметрии или просто асимметрия, обозначаемая As и вычисляемая по формуле:

.

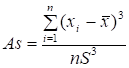
где xi — значение i-й варианты;

— среднее арифметическое;

S — среднее квадратическое отклонение;

n — объем выборки.

Для симметричной формы распределения коэффициент асимметрии равен нулю. На рис. 8 и 9. показано два асимметричных распределения. Одно из них (рис. 8) имеет положительную асимметрию (As>0), а другое (рис. 9) — отрицательную (As<0). Иногда положительную асимметрию называют левосторонней, а отрицательную — правосторонней. Смысл этого заключается в том, что максимум распределения (и большая часть вариант) смещен влево (или соответственно вправо от значения среднего арифметического.

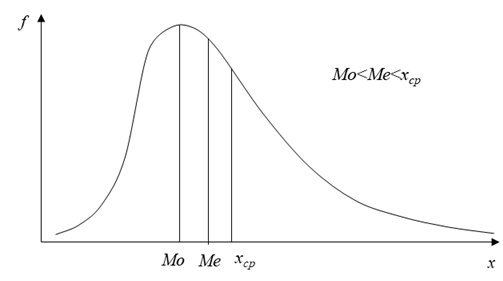
Рис. 8. Положительная (левосторонняя) асимметрия

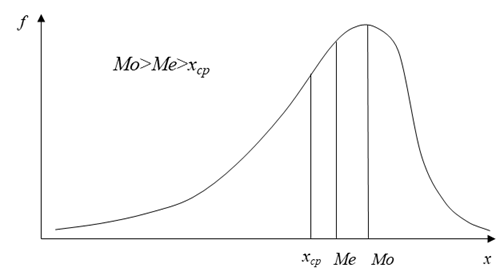
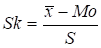
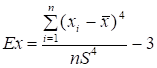
Рис. 9. Отрицательная (правосторонняя) асимметрия

Для сгруппированных данных формула для вычисления коэффициента асимметрии имеет…

Для сгруппированных данных формула для вычисления эксцесса имеет следующий вид:

.

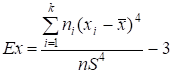
В нашем примере:

Ex=[4 (13,375−14,5331)4+8 (14,045−14,5331)4+10 (14,715−14,5331)4+.

5 (15,385−14,5331)4+2 (16,055−14,5331)4]/[29•0,73 984] - 3= -0,66.

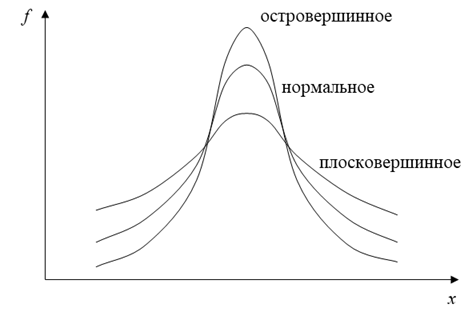
Рис. 10. Островершинное и плосковершинное распределения

Отрицательное значение эксцесса свидетельствует о наличии тенденции к плосковершинности у рассматриваемого эмпирического распределения.