Седиментация. 
Дисперсные частицы и системы

Это процесс осаждения дисперсных частиц в дисперсионной среде (обычно — в жидкости) под действием силы тяжести. Важнейшая характеристика седиментации — скорость (v) оседания индивидуальной дисперсной частицы.

Седиментация твердых частиц. Проведем расчет скорости оседания твердой сферической частицы радиусом r.

Движущая сила (f_s) создается разностью плотностей Дс = с_d — с₀ дисперсной фазы (с_d) и дисперсионной среды (с₀):

f_s = 4/3 рДсg.

где g — ускорение силы тяжести, равное 9,81 м/с².

При движении частицы в вязкой жидкости возникает противоположно направленная сила вязкого трения (f_v), ее определяет один из основных законов гидродинамики — уравнение Стокса.

Для равномерно движущегося шара уравнение Стокса имеет вид^.

f_v =6рrvз (2.7)

где з — вязкость жидкости. Па*с; v — скорость частицы; r — радиус частицы.

Уравнение Стокса (2.7) выполняется при достаточно медленном движении частицы. Необходимое условие — встречное течение жидкости, обтекающее частицу, должно быть ламинарным.

Условие ламинарности определяет неравенство: число Рейнольдса Re<1. Безразмерный критерий ламинарности (число Рейпольдса) определяется уравнением:

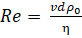
(2.8).

где d — размер частиц.

При больших скоростях седиментации Re"1 течение становится турбулентным (вихревым) и уравнение Стокса для расчета силы вязкого трения уже неприменимо.

При равномерном движении частицы с постоянной скоростью v движущая сила f_s и сила трения f_v взаимно уравновешены: f_s = f_v. Из этого условия находят скорость седиментации частицы радиусом r:

Таким образом, скорость седиментации резко растет с увеличением размера частиц (пропорционально r²). Поэтому крупные частицы оседают гораздо быстрее мелких.

Диффузия дисперсных частиц

Диффузия молекул, атомов, ионов, дисперсных частиц — один из основных процессов, происходящих в газах, жидкостях и твердых телах.

Диффузией называют самопроизвольный процесс выравнивания концентрации какого-либо вещества в газе, жидкости или твердом теле. Диффундирующее вещество может находиться в виде отдельных атомов, молекул и ионов, а также в виде дисперсных частиц. Диффузия дисперсных частиц происходит под влиянием броуновского движения и ведет к увеличению энтропии системы.

Основной закон диффузии (закон Фика) определяет количество вещества dm, которое переносится через площадь? (площадь поперечного сечения диффузионного потока) за время dt под действием градиента концентрации gradC = -dC/dx (х — направление (ось координат), в котором происходит диффузия):

Dm = -D (dC/dx)?dt (2.14)